Długość Krawędzi Podstawy Ostrosłupa Prawidłowego Czworokątnego Jest Równa 6

Dobrze, rozumiem. Oto artykuł, który przygotowałem zgodnie z Twoimi wskazówkami:

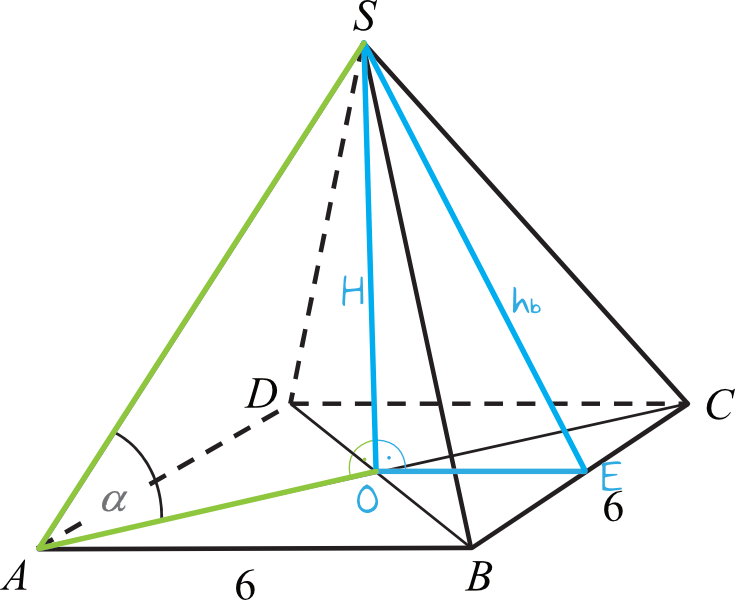
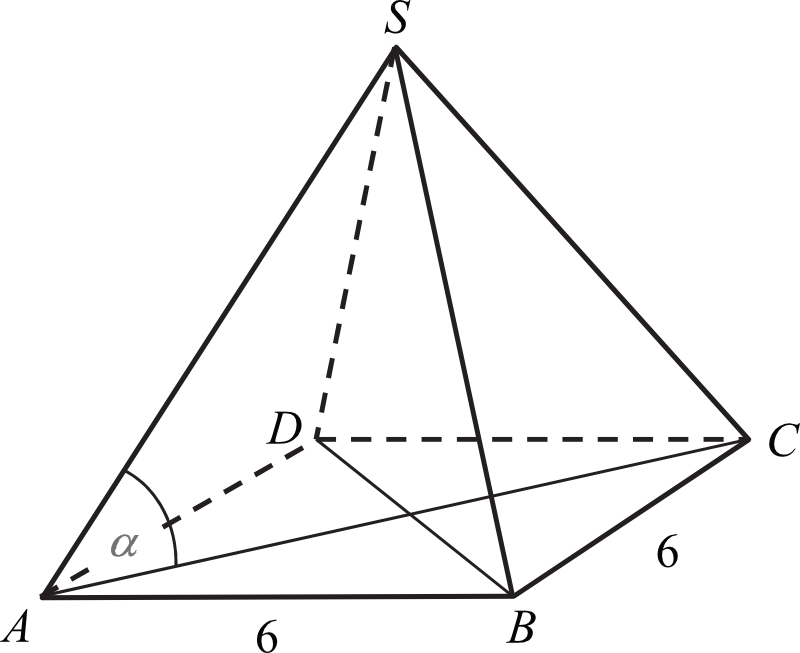
Zacznijmy od ustalenia, o czym dokładnie mówimy. Ostrosłup prawidłowy czworokątny to bryła, której podstawą jest kwadrat, a ściany boczne są przystającymi trójkątami równoramiennymi. Wszystkie ściany boczne zbiegają się w jednym punkcie, zwanym wierzchołkiem ostrosłupa. Kluczową informacją jest to, że długość krawędzi podstawy tego ostrosłupa wynosi 6.

Oznacza to, że każda strona kwadratu, który stanowi podstawę, ma długość 6 jednostek (mogą to być centymetry, metry, cale – cokolwiek). Ta informacja jest fundamentalna, ponieważ od niej zależy wiele innych obliczeń dotyczących tego ostrosłupa.

Skoro znamy długość krawędzi podstawy, możemy od razu obliczyć pole podstawy. Pole kwadratu obliczamy podnosząc długość boku do kwadratu. Zatem pole podstawy (Pp) wynosi:

Pp = 6 * 6 = 36

Pole podstawy naszego ostrosłupa wynosi 36 jednostek kwadratowych. Jest to ważne w kontekście obliczania objętości ostrosłupa, jak zobaczymy później.

Idąc dalej, możemy spróbować wyobrazić sobie, jakie inne informacje mogłyby być dla nas istotne, mając daną długość krawędzi podstawy. Zastanówmy się nad wysokością ostrosłupa. Bez dodatkowych informacji na temat wysokości ścian bocznych lub kątów nachylenia ścian bocznych do podstawy, nie możemy jej obliczyć. Wysokość ostrosłupa (H) to odległość od wierzchołka ostrosłupa do płaszczyzny podstawy, mierzona prostopadle.

Załóżmy jednak, że mamy dodatkową informację – na przykład, że wysokość ostrosłupa wynosi 8. Wtedy możemy obliczyć objętość ostrosłupa (V). Wzór na objętość ostrosłupa to:

V = (1/3) * Pp * H

Gdzie Pp to pole podstawy, a H to wysokość ostrosłupa. Podstawiając nasze wartości:

V = (1/3) * 36 * 8 = 12 * 8 = 96

Objętość ostrosłupa wynosi 96 jednostek sześciennych.

Kolejnym aspektem, który możemy rozważyć, jest wysokość ściany bocznej (h). Aby ją obliczyć, potrzebujemy znać wysokość ostrosłupa. Załóżmy ponownie, że wysokość ostrosłupa wynosi 8. Wysokość ściany bocznej, połowa długości podstawy i wysokość ostrosłupa tworzą trójkąt prostokątny. Możemy więc użyć twierdzenia Pitagorasa do obliczenia wysokości ściany bocznej.

h^2 = (a/2)^2 + H^2

Gdzie a to długość krawędzi podstawy, a H to wysokość ostrosłupa. W naszym przypadku:

h^2 = (6/2)^2 + 8^2 = 3^2 + 8^2 = 9 + 64 = 73

h = √73

Wysokość ściany bocznej wynosi √73 jednostek. Znając wysokość ściany bocznej i długość krawędzi podstawy, możemy obliczyć pole powierzchni bocznej (Pb) ostrosłupa.

Pole powierzchni bocznej ostrosłupa to suma pól wszystkich jego ścian bocznych. Ponieważ mamy ostrosłup prawidłowy czworokątny, wszystkie ściany boczne są przystającymi trójkątami. Pole jednego trójkąta to:

Pole trójkąta = (1/2) * a * h

Gdzie a to długość krawędzi podstawy, a h to wysokość ściany bocznej. W naszym przypadku:

Pole trójkąta = (1/2) * 6 * √73 = 3√73

Ponieważ mamy cztery ściany boczne, pole powierzchni bocznej wynosi:

Pb = 4 * 3√73 = 12√73

Pole powierzchni bocznej ostrosłupa wynosi 12√73 jednostek kwadratowych.

Pole Powierzchni Całkowitej

Mając pole podstawy i pole powierzchni bocznej, możemy obliczyć pole powierzchni całkowitej (Pc) ostrosłupa. Pole powierzchni całkowitej to suma pola podstawy i pola powierzchni bocznej:

Pc = Pp + Pb = 36 + 12√73

Pole powierzchni całkowitej ostrosłupa wynosi 36 + 12√73 jednostek kwadratowych.

Dalsze rozważania mogą dotyczyć kątów nachylenia ścian bocznych do podstawy lub kątów pomiędzy krawędziami bocznymi. Aby je obliczyć, potrzebowalibyśmy jednak jeszcze więcej informacji lub musielibyśmy skorzystać z funkcji trygonometrycznych. Przykładowo, tangens kąta nachylenia ściany bocznej do podstawy jest równy stosunkowi wysokości ostrosłupa do połowy długości krawędzi podstawy:

tan(α) = H / (a/2) = 8 / 3

α = arctan(8/3)

Podsumowując, z informacji o długości krawędzi podstawy ostrosłupa prawidłowego czworokątnego wynoszącej 6, mogliśmy obliczyć pole podstawy, a przy dodatkowych założeniach (np. o wysokości ostrosłupa) – objętość, wysokość ściany bocznej, pole powierzchni bocznej, pole powierzchni całkowitej oraz kąt nachylenia ściany bocznej do podstawy. Bez dodatkowych informacji, takich jak wysokość ostrosłupa lub kąty nachylenia, niektóre z tych obliczeń nie byłyby możliwe.

Zastanówmy się, co by się stało, gdybyśmy zamiast wysokości ostrosłupa znali długość krawędzi bocznej (k). Załóżmy, że krawędź boczna ma długość 10. Wtedy możemy obliczyć wysokość ostrosłupa (H) korzystając z twierdzenia Pitagorasa, ale tym razem w innym trójkącie prostokątnym – trójkącie utworzonym przez wysokość ostrosłupa, połowę przekątnej podstawy i krawędź boczną.

Przekątna podstawy (d) wynosi:

d = a√2 = 6√2

Połowa przekątnej podstawy to:

d/2 = 3√2

Zatem:

H^2 = k^2 - (d/2)^2 = 10^2 - (3√2)^2 = 100 - 18 = 82

H = √82

Teraz, znając wysokość ostrosłupa, możemy kontynuować obliczenia tak jak wcześniej, korzystając z wzoru na objętość:

V = (1/3) * Pp * H = (1/3) * 36 * √82 = 12√82

I tak dalej. Widzimy, że różne dane wejściowe prowadzą do różnych sposobów rozwiązywania problemu, ale fundamentalne zasady geometrii pozostają niezmienne. Ważne jest, aby dokładnie analizować dostępne informacje i wykorzystywać odpowiednie wzory i twierdzenia.

Zależności w Ostrosłupie Prawidłowym Czworokątnym

Warto zwrócić uwagę na zależności między różnymi elementami ostrosłupa prawidłowego czworokątnego. Wszystkie obliczenia opierają się na relacjach geometrycznych i twierdzeniach, takich jak twierdzenie Pitagorasa. Zrozumienie tych zależności pozwala na elastyczne podejście do problemów i rozwiązywanie ich różnymi metodami, w zależności od dostępnych danych.

Na przykład, jeśli znamy pole powierzchni całkowitej i długość krawędzi podstawy, możemy wyznaczyć pole powierzchni bocznej, a następnie wysokość ściany bocznej. To z kolei pozwoli nam obliczyć wysokość ostrosłupa i jego objętość. Kluczem jest identyfikacja odpowiednich trójkątów prostokątnych i stosowanie twierdzenia Pitagorasa oraz wykorzystywanie wzorów na pola i objętości.

Opanowanie tych umiejętności jest niezwykle ważne w rozwiązywaniu zadań z geometrii przestrzennej i pozwala na pełne zrozumienie właściwości ostrosłupów i innych brył geometrycznych. Analiza zależności pomiędzy elementami bryły, identyfikacja kluczowych trójkątów i stosowanie odpowiednich wzorów to podstawa skutecznego rozwiązywania zadań.