Dla Jakiej Wartości A Podany Układ Równań Jest Sprzeczny

Oto wyjaśnienie, kiedy układ równań jest sprzeczny i jak znaleźć wartość parametru, dla której tak się dzieje. Skupimy się na metodach zrozumiałych dla każdego, bez wdawania się w głębokie matematyczne teorie.

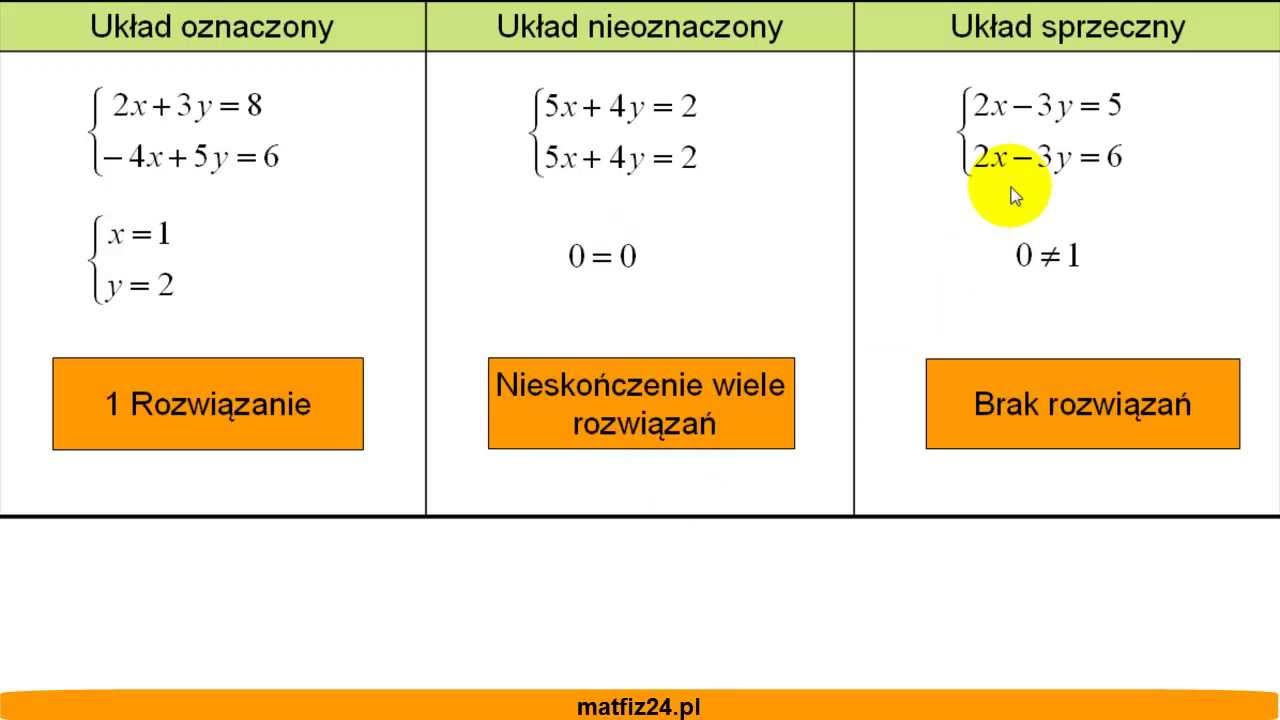
Najprościej mówiąc, układ równań jest sprzeczny, jeśli nie ma żadnego rozwiązania. Oznacza to, że nie da się znaleźć takich wartości niewiadomych (np. x i y), które spełniałyby jednocześnie wszystkie równania wchodzące w skład układu.

Wyobraźmy sobie dwa proste równania liniowe:

x + y = 5
x + y = 10

Czy istnieje para liczb x i y, która spełnia oba te równania naraz? Nie. Jeśli suma x i y ma wynosić 5, to niemożliwe jest, aby ta sama suma wynosiła 10. To właśnie przykład układu sprzecznego.

Jak sprawdzić, czy dany układ równań jest sprzeczny i jak znaleźć wartość parametru, dla której tak się dzieje? Omówimy to na konkretnych przykładach.

Załóżmy, że mamy układ równań z parametrem 'a':

ax + y = 3
2x + y = 5

Chcemy znaleźć taką wartość 'a', dla której ten układ będzie sprzeczny.

Zauważ, że jeśli współczynniki przy 'y' w obu równaniach są takie same (w tym przypadku wynoszą 1), możemy próbować doprowadzić do sytuacji, w której współczynniki przy 'x' będą proporcjonalne, ale wyrazy wolne (czyli 3 i 5) już nie. To stworzy nam sprzeczność.

Możemy spróbować wyeliminować 'y' z układu równań. Odejmijmy drugie równanie od pierwszego:

(ax + y) - (2x + y) = 3 - 5

Upraszczając:

ax - 2x = -2

Wyciągamy 'x' przed nawias:

x(a - 2) = -2

Teraz, jeśli (a - 2) byłoby równe zero, otrzymalibyśmy:

x * 0 = -2

To jest niemożliwe! Żadna liczba pomnożona przez zero nie da -2. Czyli, aby ten układ był sprzeczny, musimy mieć:

a - 2 = 0

Stąd:

a = 2

Sprawdźmy, co się stanie, gdy a = 2:

2x + y = 3
2x + y = 5

Widzimy, że mamy dokładnie taką sytuację, o której mówiliśmy na początku. Lewe strony równań są identyczne (2x + y), ale prawe strony są różne (3 i 5). Nie da się znaleźć takich x i y, które spełniałyby oba te równania jednocześnie. Zatem układ jest sprzeczny dla a = 2.

Rozwiązywanie bardziej skomplikowanych układów

A co, jeśli układ jest bardziej skomplikowany i nie widać od razu, jaka wartość parametru prowadzi do sprzeczności?

Rozważmy następujący układ:

x + ay = 4
2x + 2y = 8

W tym przypadku możemy zacząć od prostszego równania – w tym przypadku drugiego. Możemy je uprościć, dzieląc obie strony przez 2:

x + y = 4

Teraz porównajmy to z pierwszym równaniem:

x + ay = 4
x + y = 4

Jeśli a = 1, to oba równania są identyczne. Wtedy układ ma nieskończenie wiele rozwiązań (bo tak naprawdę mamy tylko jedno równanie). Ale jeśli a jest różne od 1, to układ ma jedno, konkretne rozwiązanie.

Aby znaleźć sprzeczność, musimy zmodyfikować przykład. Załóżmy, że mamy układ:

x + ay = 4
2x + 2y = 10

Dzieląc drugie równanie przez 2, otrzymujemy:

x + y = 5

Teraz porównajmy to z pierwszym równaniem:

x + ay = 4
x + y = 5

Jeśli a = 1, to mamy:

x + y = 4
x + y = 5

To jest układ sprzeczny! Zatem dla a = 1 układ jest sprzeczny.

Kluczem do rozwiązywania tego typu zadań jest manipulacja równaniami (dodawanie, odejmowanie, mnożenie, dzielenie) tak, aby doprowadzić do sytuacji, w której lewe strony równań są identyczne, a prawe strony różne. Można też próbować wyeliminować jedną ze zmiennych, tak jak pokazaliśmy w pierwszym przykładzie.

Inny przykład:

3x - y = 2
6x - ay = 5

Zauważmy, że jeśli pomnożymy pierwsze równanie przez 2, otrzymamy:

6x - 2y = 4

Teraz porównujemy to z drugim równaniem:

6x - 2y = 4
6x - ay = 5

Jeśli a = 2, to lewe strony równań są bardzo podobne. W pierwszym równaniu mamy "-2y", a w drugim "-ay". Jeśli a = 2, to lewe strony wyglądają tak:

6x - 2y = 4
6x - 2y = 5

To jest układ sprzeczny! Zatem dla a = 2 układ jest sprzeczny.

Podsumowując:

Zrozum, co oznacza sprzeczność: Układ sprzeczny to taki, który nie ma żadnego rozwiązania.
Manipuluj równaniami: Dodawaj, odejmuj, mnoż, dziel równania, aby doprowadzić do sytuacji, w której lewe strony są identyczne, a prawe różne, lub aby wyeliminować jedną ze zmiennych i dojść do niemożliwego równania.
Szukaj proporcjonalności: Zwróć uwagę, kiedy współczynniki przy zmiennych stają się proporcjonalne, ale wyrazy wolne już nie. To często prowadzi do sprzeczności.
Sprawdzaj wynik: Po znalezieniu potencjalnej wartości 'a', podstaw ją do oryginalnego układu i sprawdź, czy faktycznie prowadzi do sprzeczności.

Pamiętaj, że praktyka czyni mistrza. Im więcej rozwiążesz przykładów, tym łatwiej będzie Ci identyfikować układy sprzeczne i znajdować odpowiednie wartości parametrów. Powodzenia!