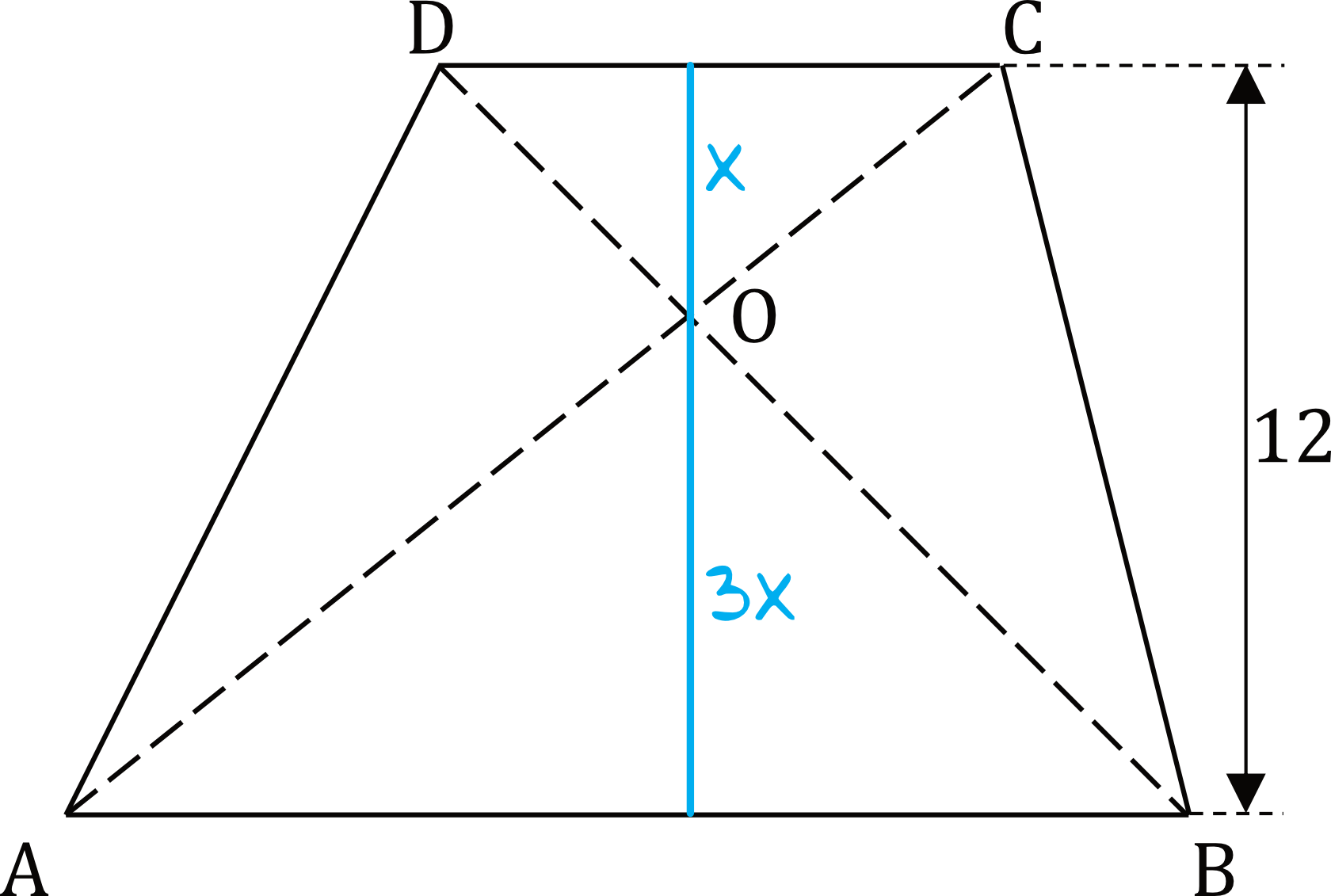
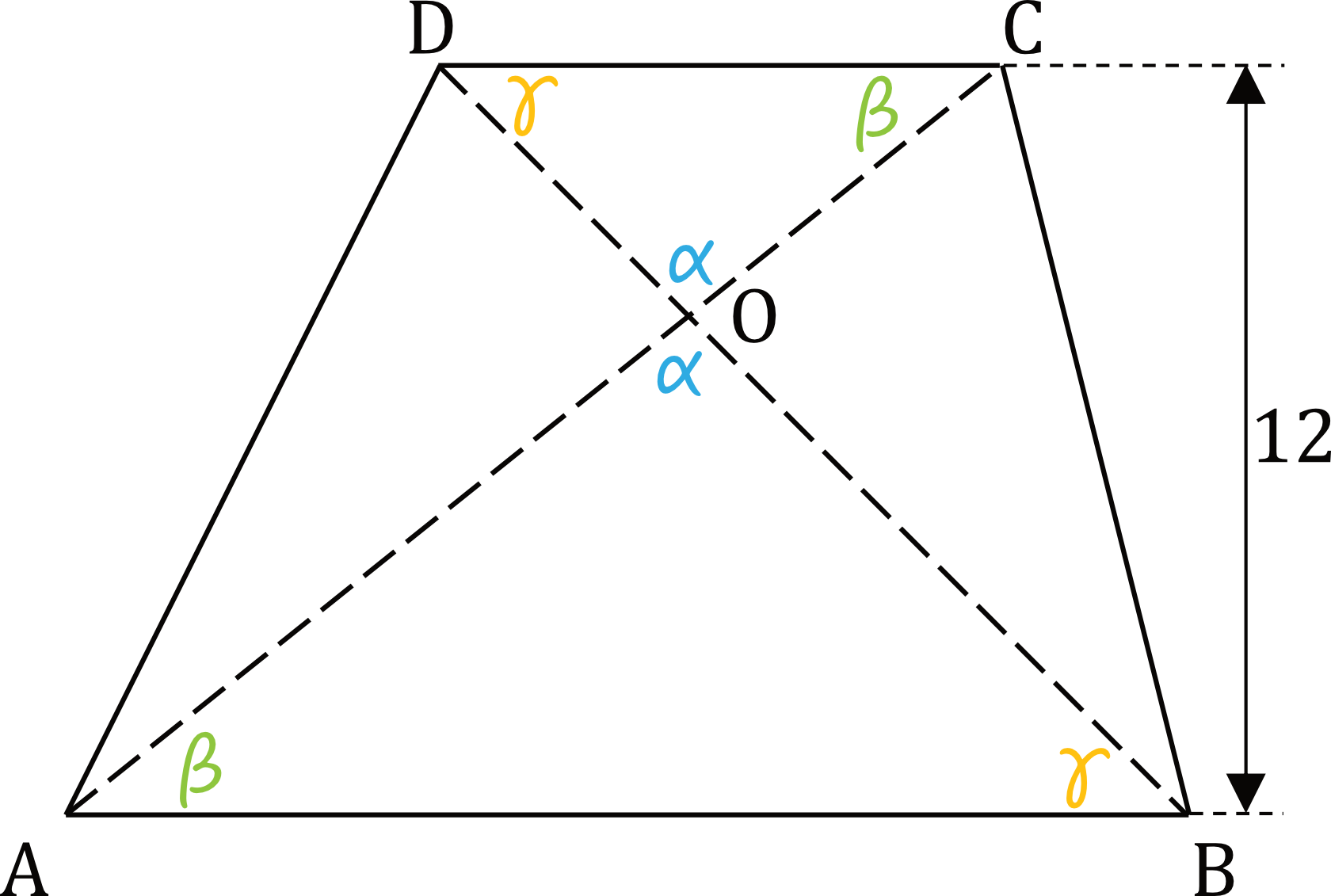
Dany Jest Trapez Abcd Na Podstawach Ab I Cd Zaznaczono

Okej, spróbujmy odpowiedzieć na pytanie dotyczące trapezu ABCD z podstawami AB i CD.

Zaznaczono. No właśnie, co zaznaczono? To kluczowe pytanie, aby móc w pełni odpowiedzieć. Bez dodatkowych informacji na temat tego, co dokładnie "zaznaczono" w trapezie ABCD, mogę jedynie przedstawić ogólne informacje i możliwości. Spróbuję przedstawić kilka scenariuszy i opisać, co mogłoby być zaznaczone oraz jakie wnioski można by z tego wyciągnąć.

Możliwe scenariusze i co można z nich wywnioskować

Zacznijmy od podstaw. Trapez to czworokąt, który ma przynajmniej jedną parę boków równoległych. Te boki równoległe nazywamy podstawami trapezu (w tym przypadku AB i CD). Pozostałe dwa boki nazywamy ramionami (AD i BC).

Załóżmy, że zaznaczono punkt E na boku AB.

Co możemy z tym zrobić?

Długości odcinków AE i EB: Jeśli znamy długości tych odcinków, możemy obliczyć długość boku AB (AB = AE + EB). Możemy również określić, w jakim stosunku punkt E dzieli bok AB. Na przykład, jeśli AE = EB, to punkt E jest środkiem boku AB.
Kąty: Jeśli zaznaczono, że jakiś kąt z wierzchołka C lub D do punktu E jest prosty, możemy mieć do czynienia z trójkątem prostokątnym. To mogłoby pomóc w obliczeniach, na przykład z wykorzystaniem twierdzenia Pitagorasa.
Prosta przechodząca przez punkt E: Jeśli narysowano prostą przechodzącą przez punkt E i równoległą do podstaw, to dzieli ona trapez na dwa mniejsze trapezy. Jeśli prosta przechodzi przez punkt E i jest prostopadła do podstaw, to mamy informację o wysokości trapezu.

Teraz załóżmy, że zaznaczono punkt F na boku CD.

Podobne wnioski jak wyżej możemy zastosować:

Długości odcinków CF i FD: Możemy obliczyć długość boku CD i określić, w jakim stosunku punkt F dzieli ten bok.
Kąty: Analogicznie jak w przypadku punktu E, kąty z wierzchołka A lub B do punktu F mogą sugerować trójkąty prostokątne lub inne relacje.
Prosta przechodząca przez punkt F: Podobne wnioski jak z prostą przechodzącą przez punkt E.

Co jeśli zaznaczono punkty na ramionach AD i BC?

Nazwijmy te punkty odpowiednio G (na AD) i H (na BC).

Odcinki AG, GD, BH, HC: Podobnie jak wcześniej, możemy analizować proporcje, w jakich punkty dzielą ramiona trapezu.
Czworokąty: Zaznaczenie punktów G i H tworzy czworokąt GBCH. Jeśli wiemy coś o jego kątach lub bokach, możemy wykorzystać tę wiedzę do dalszych obliczeń.
Linie łączące G i H: Jeśli linia GH jest równoległa do podstaw AB i CD, to tworzy kolejny trapez AGHD i GBCH. Może to prowadzić do relacji podobieństwa pomiędzy trapezami.

Przekątne i ich punkty przecięcia

Załóżmy, że zaznaczono punkt przecięcia przekątnych AC i BD (nazwijmy go punktem O).

Podobieństwo trójkątów: Trójkąty AOB i COD są podobne. To wynika z faktu, że AB jest równoległe do CD, co implikuje równość kątów naprzemianległych. Możemy wtedy ustalić proporcje między bokami tych trójkątów.
Dzielenie przekątnych: Punkt O dzieli przekątne w pewnym stosunku. Stosunek ten jest związany z długościami podstaw AB i CD.
Wysokość trapezu: Jeśli znamy odległość punktu O od podstaw AB i CD, możemy wnioskować o wysokości całego trapezu.

Środki Boków Nierównoległych i Inne Ważne Punkty

Często w zadaniach z trapezami zaznacza się środki boków nierównoległych (ramion). Nazwijmy środek AD jako punkt K, a środek BC jako punkt L.

Odcinek KL (linia środkowa): Odcinek łączący środki ramion trapezu nazywany jest linią środkową. Linia środkowa jest równoległa do podstaw i jej długość jest równa średniej arytmetycznej długości podstaw: KL = (AB + CD) / 2. Jest to bardzo użyteczna własność przy rozwiązywaniu zadań.
Punkt przecięcia KL z przekątnymi: Linia środkowa przecina przekątne trapezu. Można analizować, w jakim stosunku punkty przecięcia dzielą przekątne i linię środkową.

Wysokość trapezu

Często zaznacza się wysokość trapezu, czyli odcinek prostopadły do podstaw, łączący jedną podstawę z drugą. Wysokość może być poprowadzona z dowolnego wierzchołka.

Pole trapezu: Znając długość podstaw (AB i CD) oraz wysokość (h), możemy obliczyć pole trapezu: P = (AB + CD) * h / 2.
Trójkąty prostokątne: Wysokość trapezu tworzy trójkąty prostokątne przy ramionach. Można wykorzystać twierdzenie Pitagorasa do obliczenia długości ramion, jeśli znamy inne informacje.

Co jeszcze można zaznaczyć?

To zależy od konkretnego zadania. Mogą to być:

Kąty: Zaznaczone kąty mogą wskazywać na równoramienność trapezu (jeśli kąty przy jednej podstawie są równe) lub na inne zależności geometryczne.
Pola trójkątów: Zaznaczenie pola jakiegoś trójkąta wewnątrz trapezu może dać nam informacje potrzebne do obliczenia innych pól lub długości.
Promień okręgu wpisanego lub opisanego: Jeśli w trapez można wpisać okrąg, to suma długości podstaw jest równa sumie długości ramion: AB + CD = AD + BC. Jeśli na trapezie można opisać okrąg, to jest to trapez równoramienny.

Podsumowując, bez konkretnej informacji, co "zaznaczono" w trapezie ABCD, trudno udzielić precyzyjnej odpowiedzi. Przedstawiłem szereg możliwości i potencjalnych wniosków, które można z nich wyciągnąć. Ważne jest, aby analizować rysunek, szukać związków geometrycznych, zależności pomiędzy kątami i bokami, oraz wykorzystywać znane wzory i twierdzenia dotyczące trapezów. Kluczem jest identyfikacja, co dokładnie zostało zaznaczone i jak ta informacja wiąże się z resztą rysunku i pytaniem zadania.