Dany Jest Ostrosłup Prawidłowy Czworokątny Abcds O Podstawie Abcd

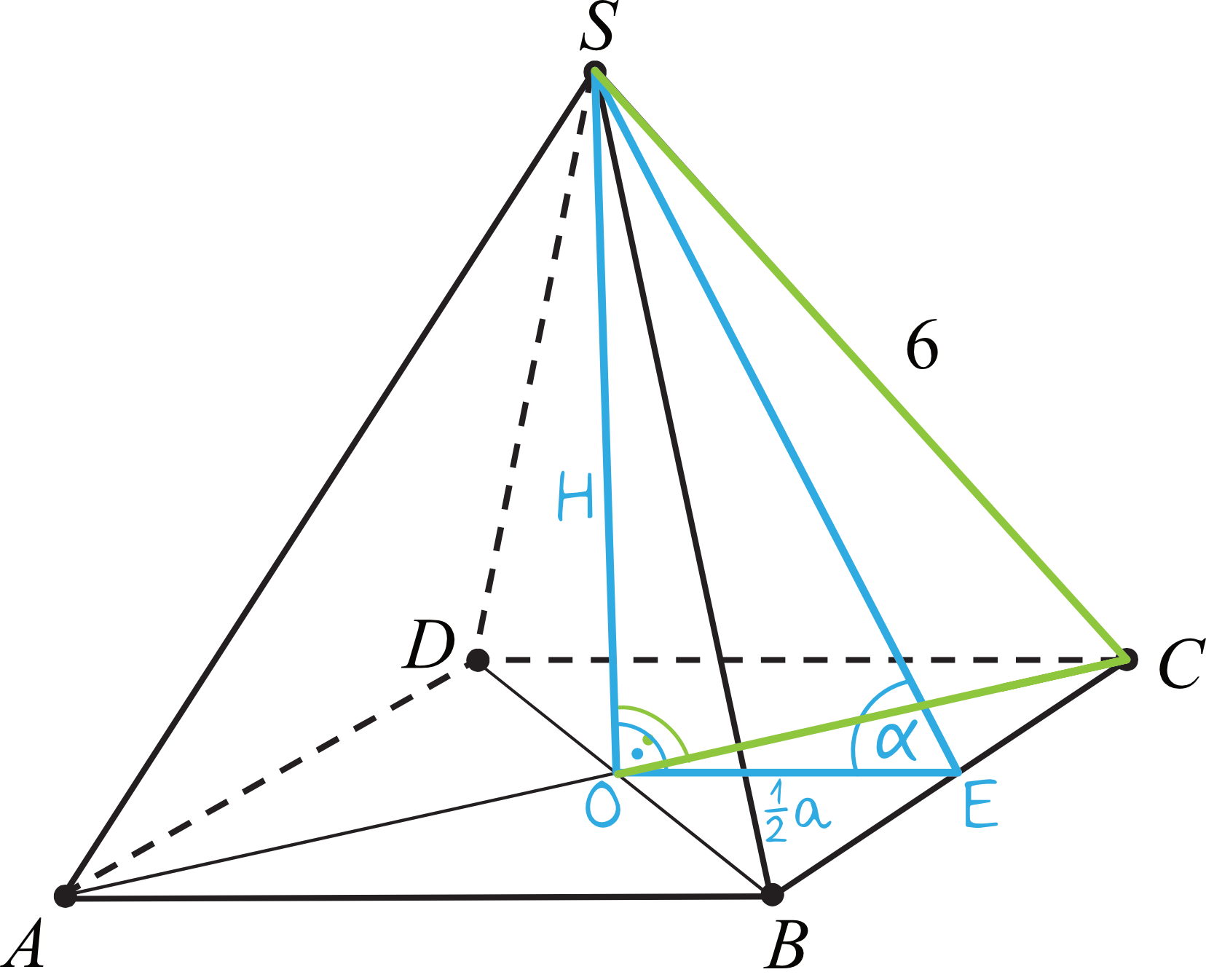
Dobrze, spróbujmy wyjaśnić, czym jest ostrosłup prawidłowy czworokątny ABCD, o podstawie ABCD.

Zacznijmy od podstaw. Wyobraź sobie piramidę. To jest dobry obraz, żeby zrozumieć, czym jest ostrosłup. Ostrosłup to bryła, która ma jedną podstawę (w naszym przypadku czworokąt ABCD) i ściany boczne, które zbiegają się w jednym punkcie, nazywanym wierzchołkiem ostrosłupa (S w naszym przypadku Abcds).

Teraz skupmy się na tym, co oznacza "prawidłowy czworokątny". "Czworokątny" oznacza, że podstawa ostrosłupa jest czworokątem, czyli figurą geometryczną mającą cztery boki i cztery kąty. "Prawidłowy" w tym kontekście jest bardzo ważny. Mówi nam, że podstawa jest kwadratem. Kwadrat ma wszystkie boki równe i wszystkie kąty proste (90 stopni). To upraszcza nam sprawę, bo wiemy, że ABCD to kwadrat.

Czyli, żeby podsumować, ostrosłup prawidłowy czworokątny Abcds ma podstawę, która jest kwadratem ABCD. Ściany boczne są trójkątami, które spotykają się w punkcie S. Ale to jeszcze nie wszystko. W ostrosłupie prawidłowym, spodek wysokości (czyli punkt, w którym wysokość ostrosłupa opada na podstawę) znajduje się w środku kwadratu ABCD. To znaczy, że linia prosta narysowana z wierzchołka S prostopadle do podstawy trafi dokładnie w środek kwadratu. To bardzo ważne, bo wpływa na obliczenia i symetrię ostrosłupa.

Co to dla nas znaczy? Oznacza to, że jeśli mamy ostrosłup prawidłowy czworokątny, to możemy skorzystać z różnych zależności geometrycznych, żeby obliczyć jego objętość, pole powierzchni, długości krawędzi i inne parametry. Znając długość boku kwadratu (podstawy) i wysokość ostrosłupa, możemy obliczyć wszystko inne.

Własności i Wyliczenia

Teraz porozmawiajmy o tym, co możemy obliczyć i jakie własności ma taki ostrosłup.

Objętość: Objętość ostrosłupa obliczamy ze wzoru: V = (1/3) * Pp * H, gdzie Pp to pole powierzchni podstawy, a H to wysokość ostrosłupa. W naszym przypadku, ponieważ podstawa jest kwadratem o boku a, pole powierzchni podstawy wynosi Pp = a². Zatem, objętość ostrosłupa prawidłowego czworokątnego wynosi V = (1/3) * a² * H.
Pole Powierzchni: Pole powierzchni ostrosłupa to suma pola powierzchni podstawy i pola powierzchni wszystkich ścian bocznych. W naszym przypadku mamy cztery identyczne trójkąty równoramienne. Pole powierzchni całkowitej (Pc) to więc: Pc = Pp + 4 * Pb, gdzie Pb to pole powierzchni jednej ściany bocznej. Żeby obliczyć pole ściany bocznej, potrzebujemy znać długość boku podstawy (a) i wysokość ściany bocznej (oznaczmy ją jako h). Wtedy Pb = (1/2) * a * h. Zatem, Pc = a² + 4 * (1/2) * a * h = a² + 2ah.
Wysokość ściany bocznej (h): Wysokość ściany bocznej h tworzy trójkąt prostokątny z połową boku podstawy (a/2) i wysokością ostrosłupa (H). Możemy tutaj użyć twierdzenia Pitagorasa: (a/2)² + H² = h². Zatem h = √( (a/2)² + H² ).
Długość Krawędzi Bocznej (k): Krawędź boczna k to odległość od wierzchołka S do wierzchołka kwadratu A, B, C lub D. Krawędź boczna również tworzy trójkąt prostokątny z połową przekątnej kwadratu i wysokością ostrosłupa. Przekątna kwadratu o boku a wynosi a√2. Zatem połowa przekątnej to (a√2)/2. Używając twierdzenia Pitagorasa: ((a√2)/2)² + H² = k². Zatem k = √( (a²/2) + H² ).
Spodek wysokości: Jak już wspomnieliśmy, spodek wysokości ostrosłupa prawidłowego czworokątnego znajduje się w środku kwadratu. Oznacza to, że jeśli narysujemy odcinek od wierzchołka S do środka kwadratu ABCD, to ten odcinek będzie prostopadły do podstawy. Ten odcinek jest wysokością ostrosłupa.

Przykładowe Zadanie

Załóżmy, że mamy ostrosłup prawidłowy czworokątny, gdzie bok podstawy (a) wynosi 6 cm, a wysokość ostrosłupa (H) wynosi 4 cm. Obliczmy objętość i pole powierzchni całkowitej.

Objętość: V = (1/3) * a² * H = (1/3) * 6² * 4 = (1/3) * 36 * 4 = 48 cm³.
Wysokość ściany bocznej: h = √( (a/2)² + H² ) = √( (6/2)² + 4² ) = √( 3² + 16 ) = √( 9 + 16 ) = √25 = 5 cm.
Pole powierzchni całkowitej: Pc = a² + 2ah = 6² + 2 * 6 * 5 = 36 + 60 = 96 cm².

Ważne jest, żeby pamiętać o jednostkach. Objętość podajemy w centymetrach sześciennych (cm³), a pole powierzchni w centymetrach kwadratowych (cm²).

Podsumowując, ostrosłup prawidłowy czworokątny to bryła, która ma bardzo regularną budowę, co ułatwia obliczenia. Znając definicję i kilka podstawowych wzorów, możemy rozwiązać wiele problemów związanych z tą figurą geometryczną. Kluczem jest zrozumienie, co oznacza słowo "prawidłowy" i jak ono wpływa na własności ostrosłupa.

Mam nadzieję, że to wyjaśnienie było pomocne! Pamiętajcie, żeby ćwiczyć na przykładach, żeby lepiej zrozumieć te zagadnienia. Powodzenia!