Czy Suma Dwóch Liczb Wymiernych Jest Zawsze Liczbą Wymierną

Oczywiście, oto artykuł na temat sumy dwóch liczb wymiernych, napisany w języku polskim, prostym językiem i zgodnie z Twoimi instrukcjami:

Zastanówmy się, co się stanie, gdy dodamy do siebie dwie liczby wymierne. Czy wynik zawsze będzie liczbą wymierną? Odpowiedź brzmi: tak! Ale żeby to lepiej zrozumieć, przyjrzyjmy się bliżej liczbom wymiernym i jak je dodajemy.

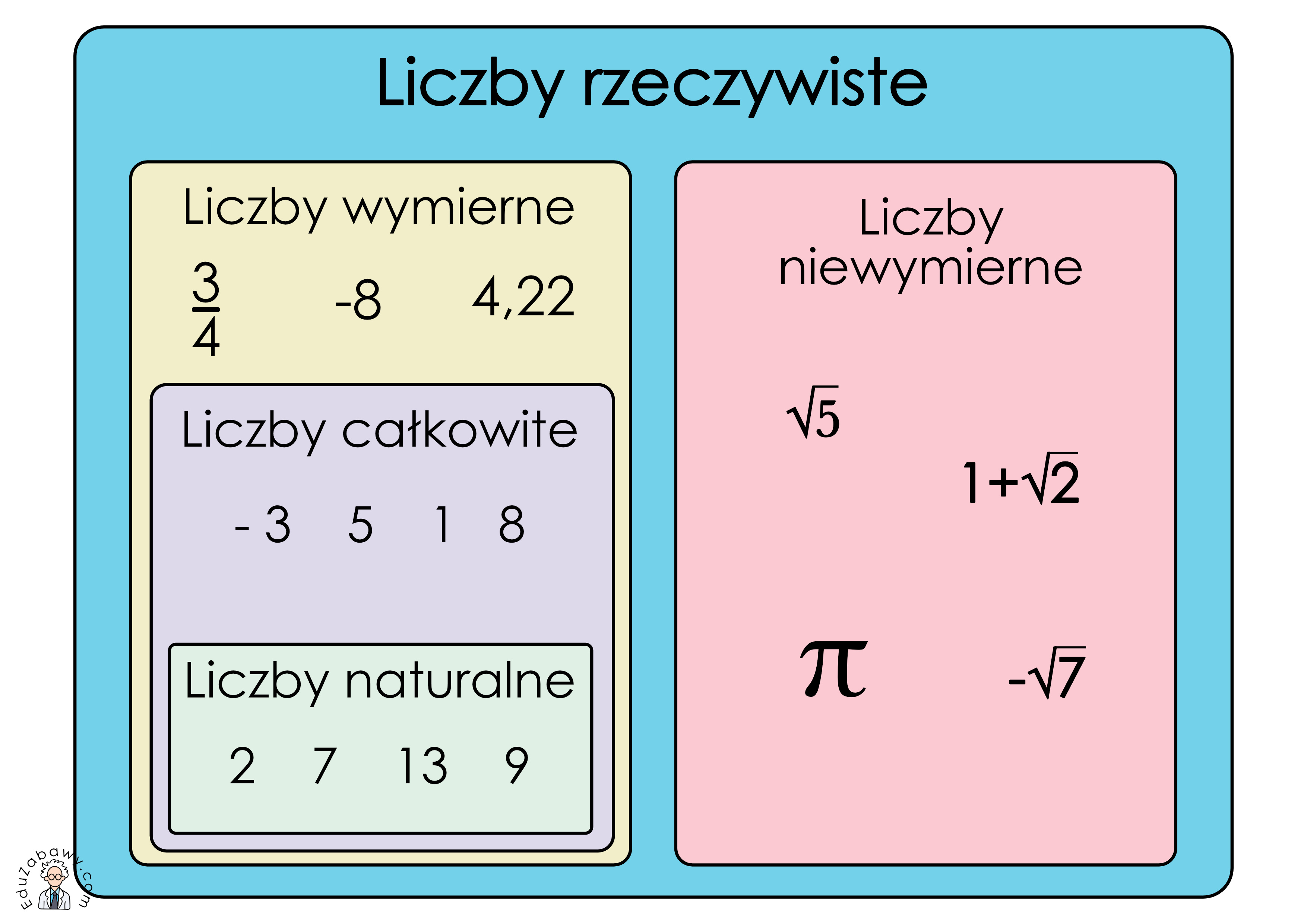
Liczba wymierna to taka, którą możemy zapisać jako ułamek, gdzie licznik i mianownik są liczbami całkowitymi, a mianownik nie jest zerem. Na przykład, 1/2, 3/4, -5/7, 2 (bo 2 to to samo co 2/1), a nawet 0 (bo 0 to to samo co 0/1) to liczby wymierne. Ważne jest, żeby mianownik nigdy nie był zerem, bo dzielenie przez zero jest niedozwolone w matematyce.

Jak więc dodajemy do siebie ułamki, czyli liczby wymierne? Najprościej jest, gdy ułamki mają ten sam mianownik. Wtedy po prostu dodajemy liczniki, a mianownik zostaje ten sam. Na przykład:

1/5 + 2/5 = (1+2)/5 = 3/5

Wynik (3/5) jest również ułamkiem, więc jest liczbą wymierną.

A co, jeśli ułamki mają różne mianowniki? Wtedy musimy je najpierw sprowadzić do wspólnego mianownika. Oznacza to, że musimy znaleźć taki mianownik, który dzieli się zarówno przez jeden, jak i drugi mianownik. Najczęściej szukamy najmniejszego wspólnego mianownika, ale każdy wspólny mianownik zadziała. Spójrzmy na przykład:

1/2 + 1/3

Mianowniki to 2 i 3. Najmniejszy wspólny mianownik to 6 (bo 6 dzieli się przez 2 i przez 3). Teraz musimy przekształcić oba ułamki tak, żeby miały mianownik 6.

Żeby z 1/2 zrobić ułamek o mianowniku 6, musimy pomnożyć zarówno licznik, jak i mianownik przez 3:

1/2 * (3/3) = 3/6

(Pamiętaj, że mnożenie przez 3/3 to tak naprawdę mnożenie przez 1, więc wartość ułamka się nie zmienia.)

Żeby z 1/3 zrobić ułamek o mianowniku 6, musimy pomnożyć zarówno licznik, jak i mianownik przez 2:

1/3 * (2/2) = 2/6

Teraz możemy dodać ułamki:

3/6 + 2/6 = (3+2)/6 = 5/6

Wynik (5/6) jest również ułamkiem, więc jest liczbą wymierną.

Przykłady z liczbami ujemnymi i zerem

Co się stanie, jeśli dodamy liczby wymierne ujemne lub zero? Zasady są takie same. Pamiętaj, że liczby ujemne też mogą być zapisane jako ułamki. Na przykład, -2 to to samo co -2/1.

Spójrzmy na przykład z liczbą ujemną:

1/4 + (-3/4) = (1 + (-3))/4 = -2/4

Wynik (-2/4) jest liczbą wymierną. Możemy go jeszcze uprościć do -1/2, co też jest liczbą wymierną.

A co z zerem?

1/2 + 0 = 1/2 + 0/1 = 1/2

(ponieważ 0 pomnożone przez cokolwiek daje 0)

Wynik (1/2) jest nadal liczbą wymierną.

Ważne wnioski

Podsumowując, dodając dwie liczby wymierne, zawsze otrzymamy liczbę wymierną. Dzieje się tak dlatego, że:

1. Liczby wymierne to ułamki.
2. Dodawanie ułamków (po sprowadzeniu do wspólnego mianownika) daje w wyniku ułamek.
3. Ułamek, w którym licznik i mianownik są liczbami całkowitymi (i mianownik nie jest zerem), jest liczbą wymierną.

Nieważne, czy dodajemy ułamki dodatnie, ujemne, czy zera, wynik zawsze będzie ułamkiem, a więc liczbą wymierną. Możemy też myśleć o tym w ten sposób: jeśli mamy dwie liczby, które możemy dokładnie wyrazić za pomocą proporcji liczb całkowitych, to ich suma też musi dać się wyrazić za pomocą proporcji liczb całkowitych.

Pamiętajmy, że ten fakt jest bardzo ważny w matematyce. Pokazuje on, że zbiór liczb wymiernych jest "zamknięty" ze względu na operację dodawania. Oznacza to, że wykonując dodawanie na liczbach wymiernych, nigdy nie "wyjdziemy" poza zbiór liczb wymiernych. Zawsze pozostaniemy w świecie liczb wymiernych.

To jest fundament algebraiczny, który pomaga nam rozumieć bardziej złożone pojęcia matematyczne.