Czy Romb Jest Trapezem Równoramiennym

Zastanawiasz się, czy romb może być jednocześnie trapezem równoramiennym? To pytanie, które często pojawia się na lekcjach geometrii i może sprawiać pewne trudności. Wbrew pozorom, odpowiedź nie jest tak prosta, jak mogłoby się wydawać. W tym artykule postaramy się rozwiać wszelkie wątpliwości i zrozumieć, dlaczego odpowiedź jest bardziej skomplikowana i dlaczego ten temat może mieć znaczenie, nawet poza szkolną ławką.

Wyobraź sobie sytuację: projektujesz ogród i chcesz ułożyć ścieżkę z płyt w kształcie rombów. Jednak w pewnym miejscu ścieżka musi płynnie przejść w trapez równoramienny. Czy płytki rombowe się do tego nadają? A może budujesz domek dla lalek i zastanawiasz się, jak wyciąć idealne okno, które ma być jednocześnie rombem i trapezem. Brzmi absurdalnie? Może i tak, ale zrozumienie relacji między różnymi figurami geometrycznymi pozwala na kreatywne rozwiązywanie problemów w wielu dziedzinach, od projektowania, przez architekturę, po nawet programowanie grafiki komputerowej.

Definicje – Klucz do zrozumienia

Zanim odpowiemy na główne pytanie, uporządkujmy definicje. To fundament naszej dyskusji.

Romb

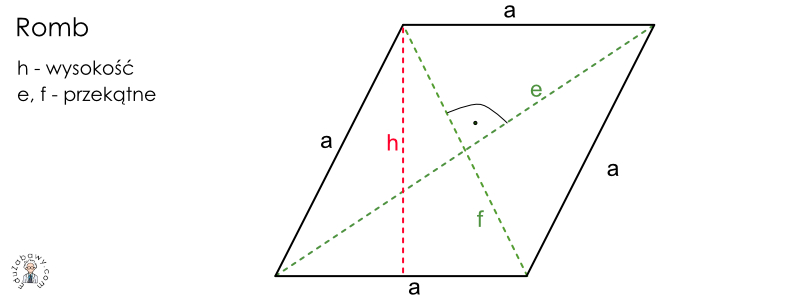
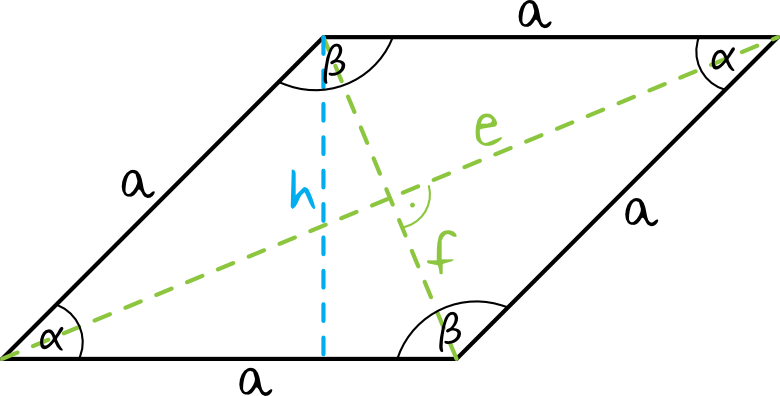
Romb to czworokąt, który ma wszystkie boki równe. Jego przekątne przecinają się pod kątem prostym i dzielą na połowy. Kąty przeciwległe w rombie są równe.

Trapez Równoramienny

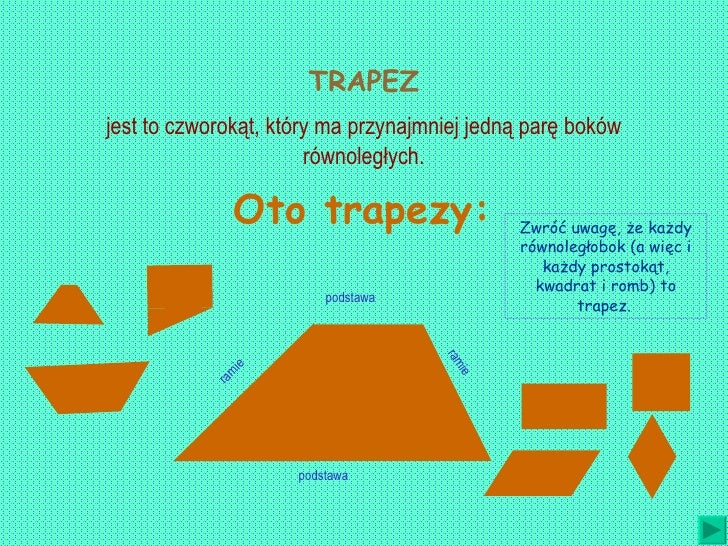
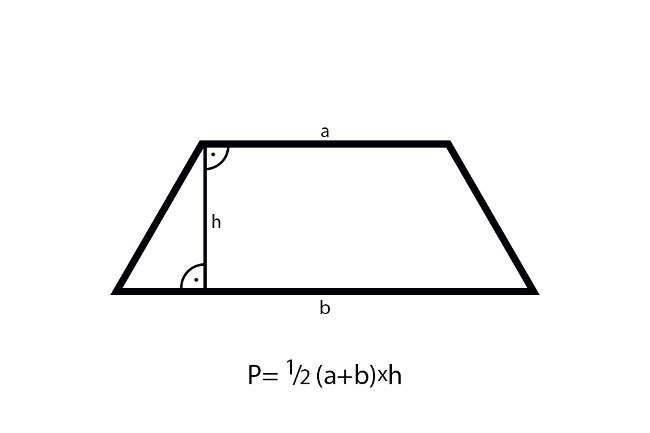
Trapez równoramienny to trapez (czyli czworokąt mający co najmniej jedną parę boków równoległych), którego ramiona (boki nierównoległe) są równe. Kąty przy każdej z podstaw są równe.

Zauważ, że definicja trapezu wymaga tylko *jednej* pary boków równoległych. To istotny punkt.

Analiza Możliwości

Czy romb może spełniać definicję trapezu równoramiennego? Spróbujmy to rozważyć:

Boki równoległe: Romb ma dwie pary boków równoległych. Zatem, *z definicji*, jest trapezem (bo ma przynajmniej jedną parę boków równoległych).
Ramiona równe: W rombie wszystkie boki są równe. Czyli, w szczególnym przypadku, kiedy romb jest trapezem, jego ramiona (boki nierównoległe) również są równe.
Kąty przy podstawach: W trapezie równoramiennym kąty przy każdej z podstaw są równe. W rombie, kąty przeciwległe są równe. Aby romb był trapezem równoramiennym, te kąty muszą być odpowiednio ułożone.

Wniosek? Romb może być trapezem równoramiennym, ale tylko w specjalnym przypadku.

Kiedy Romb JEST Trapezem Równoramiennym? – Szczególne Przypadki

Kluczowe jest zrozumienie, kiedy romb staje się szczególnym przypadkiem trapezu równoramiennego.

Kwadrat: Najprostszy przykład. Kwadrat to romb o wszystkich kątach prostych. Jest też prostokątem o wszystkich bokach równych. Kwadrat ma dwie pary boków równoległych (spełnia definicję trapezu) i wszystkie boki równe (spełnia warunek równoramienności). Kąty przy podstawach są równe (oba równe 90 stopniom). Zatem, kwadrat jest trapezem równoramiennym.
Prostokąt (który jest kwadratem): Jak wspomniano wyżej, kwadrat jest również prostokątem.

Zatem, romb jest trapezem równoramiennym **tylko wtedy, gdy jest kwadratem.**

Dlaczego Nie Każdy Romb Jest Trapezem Równoramiennym?

Rozważmy romb, który **nie** jest kwadratem. Oznacza to, że jego kąty nie są proste.

Aby był trapezem równoramiennym, musiałby spełniać warunek równości kątów przy podstawach. Jednak w rombie, którego kąty nie są proste, kąty przy "podstawie" (boku równoległym do innego boku) nie będą równe. Dwa kąty będą ostre, a dwa rozwarte. Dlatego **nie może** być trapezem równoramiennym.

Kontrargumenty i Drobne Niuanse

Możesz spotkać się ze stwierdzeniem, że równoległobok (czyli czworokąt mający dwie pary boków równoległych) jest szczególnym przypadkiem trapezu. I to prawda, jeśli przyjmiemy definicję trapezu, która mówi, że trapez ma *przynajmniej* jedną parę boków równoległych. Jednak, tradycyjnie, trapez definiuje się jako czworokąt, który ma *dokładnie* jedną parę boków równoległych. Wówczas, równoległobok (w tym romb) nie jest trapezem.

Dlatego, kluczowe jest zrozumienie, jakiej definicji trapezu używamy. Większość podręczników szkolnych przyjmuje definicję "przynajmniej jedna para boków równoległych", co sprawia, że romb *potencjalnie* może być trapezem.

Wpływ na codzienne życie? Więcej niż myślisz!

Może się wydawać, że rozważania o tym, czy romb jest trapezem równoramiennym, to czysta teoria. Nic bardziej mylnego! Zrozumienie relacji między figurami geometrycznymi ma ogromny wpływ na wiele dziedzin:

Architektura i Budownictwo: Projektowanie elewacji, układanie płytek, obliczanie kątów nachylenia – wszystko to wymaga znajomości geometrii.
Projektowanie Graficzne: Tworzenie logo, ilustracji, animacji – figury geometryczne są podstawą wielu projektów.
Programowanie Gier: Wykorzystywanie geometrii do tworzenia realistycznych środowisk i interakcji.
Matematyka Finansowa: Modelowanie wzrostu i spadku cen, obliczanie ryzyka – geometria odgrywa rolę w wizualizacji danych i tworzeniu modeli.

Nawet tak abstrakcyjne zagadnienie jak relacja rombu i trapezu równoramiennego, rozwija logiczne myślenie i umiejętność analizowania problemów – kompetencje cenne w każdym zawodzie.

Podsumowanie i Odpowiedź

Wróćmy do naszego głównego pytania: Czy romb jest trapezem równoramiennym?

Odpowiedź brzmi: Tak, ale tylko wtedy, gdy jest kwadratem. Kwadrat spełnia wszystkie kryteria zarówno rombu, jak i trapezu równoramiennego.

Pamiętaj, że definicje są kluczowe. Przyjmując definicję trapezu jako czworokąta mającego *przynajmniej* jedną parę boków równoległych, romb potencjalnie może być trapezem (w szczególnym przypadku – kwadratem). Jeśli natomiast trapez definiujemy jako czworokąt mający *dokładnie* jedną parę boków równoległych, romb nigdy nie będzie trapezem.

Co Dalej?

Mam nadzieję, że ten artykuł pomógł Ci zrozumieć relację między rombem a trapezem równoramiennym. Zachęcam Cię do dalszego zgłębiania wiedzy z geometrii. Spróbuj:

Narysuj różne romby i trapezy równoramienne. Zastanów się, kiedy romb może "zamienić się" w trapez równoramienny.
Poszukaj w swoim otoczeniu przykładów rombów i trapezów. Zwróć uwagę na to, jakie cechy decydują o tym, że dana figura jest rombem, a inna trapezem.
Rozwiąż zadania z geometrii, które łączą różne figury geometryczne.

Czy teraz, patrząc na kwadratową płytkę chodnikową, pomyślisz o niej jak o szczególnym przypadku rombu i trapezu równoramiennego?