Czy Przekatne W Rownolegloboku Dziela Sie Na Polowy

Hej Studenci! Przygotowujecie się do sprawdzianu z geometrii? Świetnie! Dzisiaj skupimy się na jednym z kluczowych zagadnień dotyczących równoległoboków: czy przekątne w równoległoboku dzielą się na połowy? Odpowiedź jest prosta: TAK! Ale żeby to zrozumieć dogłębnie i umieć udowodnić, przejdźmy przez to razem krok po kroku. Nie martwcie się, damy radę! Będziemy tłumaczyć wszystko powoli i z przykładami.

Czym jest Równoległobok?

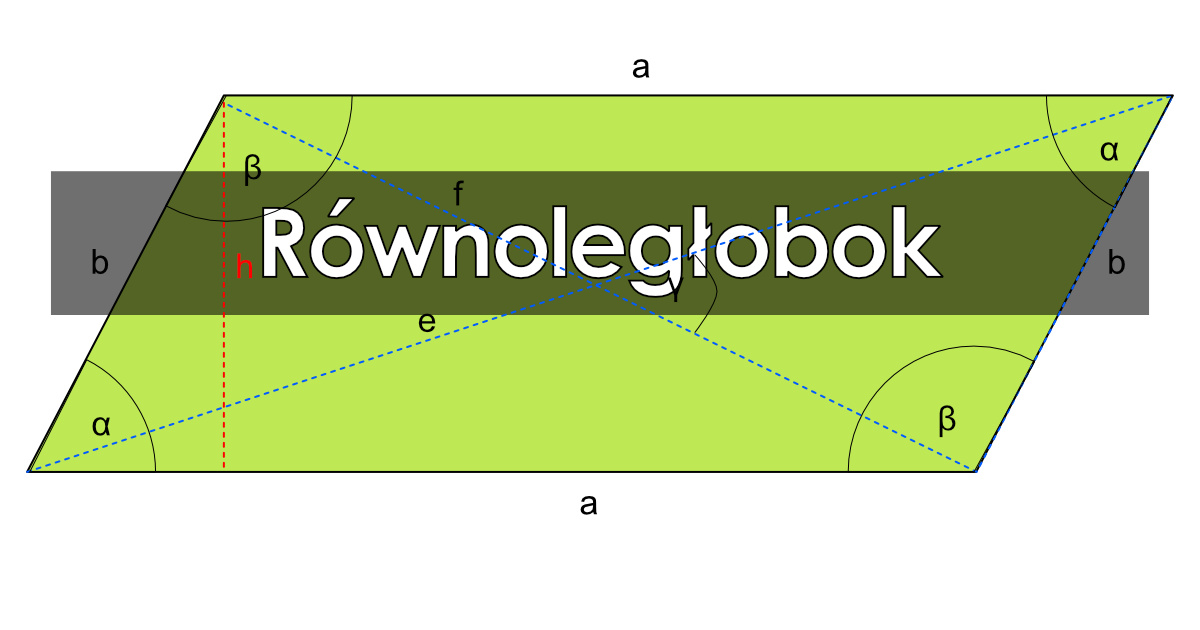
Zacznijmy od podstaw. Równoległobok to czworokąt, który ma następujące cechy:

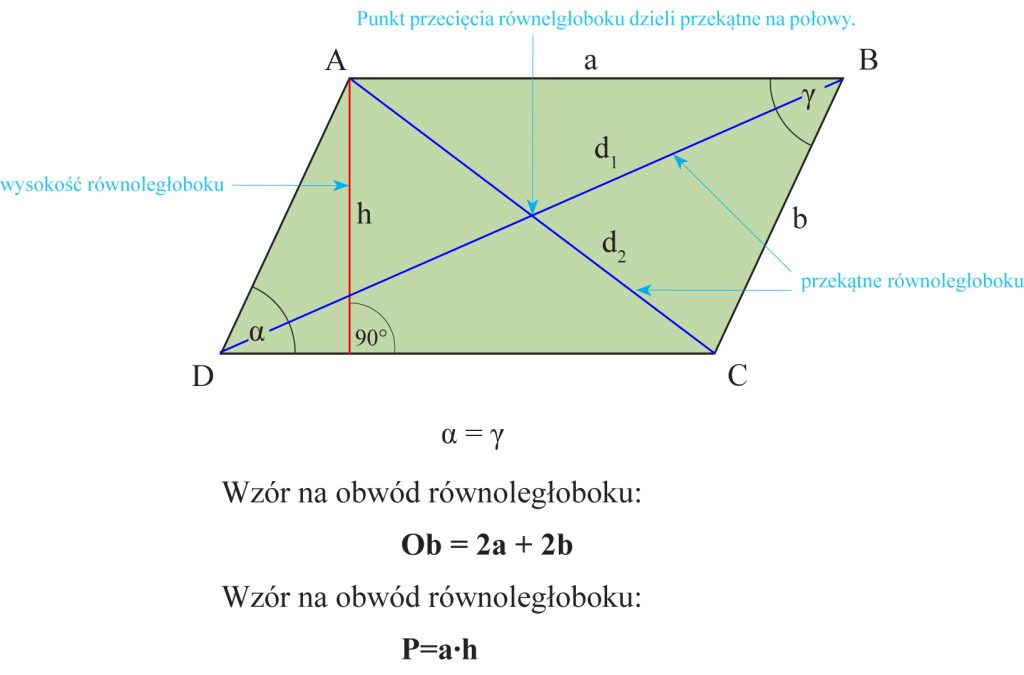
Dwie pary boków równoległych: To kluczowa cecha definiująca równoległobok. Oznacza to, że bok AB jest równoległy do boku CD, a bok AD jest równoległy do boku BC.
Dwie pary boków równych: Boki przeciwległe są nie tylko równoległe, ale również równej długości. Czyli |AB| = |CD| i |AD| = |BC|.
Przeciwległe kąty są równe: Kąt przy wierzchołku A jest równy kątowi przy wierzchołku C, a kąt przy wierzchołku B jest równy kątowi przy wierzchołku D.
Suma kątów wewnętrznych wynosi 360 stopni: Jak w każdym czworokącie.

Pamiętajcie! Kwadrat, prostokąt i romb to szczególne przypadki równoległoboku. Mają wszystkie cechy równoległoboku, ale dodatkowo posiadają specyficzne właściwości (np. wszystkie kąty proste w kwadracie i prostokącie, wszystkie boki równe w kwadracie i rombie).

Co to są Przekątne?

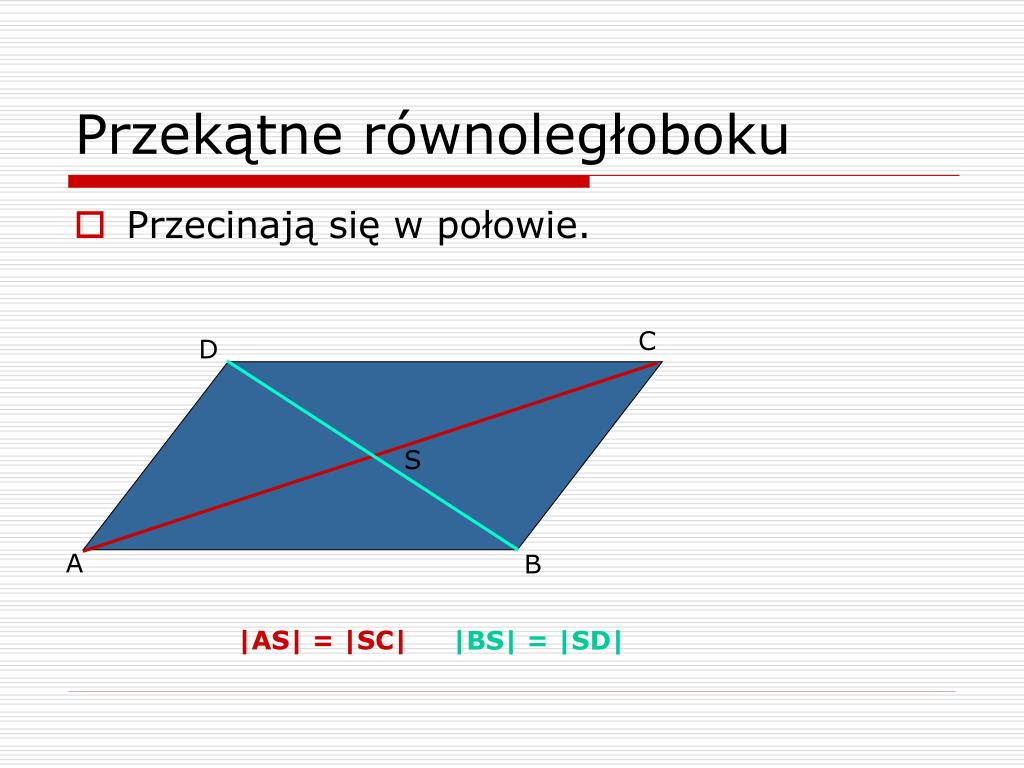
Przekątna to odcinek łączący dwa wierzchołki wielokąta, które nie są ze sobą sąsiadujące. W równoległoboku mamy dwie przekątne: AC i BD. Punkt, w którym te przekątne się przecinają, nazwijmy go punktem O.

Twierdzenie o Przekątnych w Równoległoboku

Twierdzenie: Przekątne w równoległoboku przecinają się w połowie. To oznacza, że punkt O dzieli każdą z przekątnych na dwie równe części. Innymi słowy: |AO| = |OC| oraz |BO| = |OD|.

Dowód Twierdzenia

Teraz przejdźmy do dowodu, żebyście mieli pewność, skąd to się bierze. Dowód jest bardzo ważny, bo pokazuje, że nie tylko pamiętamy fakt, ale też rozumiemy, dlaczego tak jest.

Rozważmy równoległobok ABCD. Przekątne AC i BD przecinają się w punkcie O. Chcemy udowodnić, że |AO| = |OC| oraz |BO| = |OD|.

Krok 1: Wybierzmy Trójkąty

Spójrzmy na trójkąty AOB i COD. Spróbujemy pokazać, że są one przystające.

Krok 2: Ustalmy Cechy Przystawania
- Kąty:
  - Kąt OAB jest równy kątowi OCD (są to kąty naprzemianległe utworzone przez przecięcie prostych równoległych AB i CD prostą AC).
  - Kąt ABO jest równy kątowi CDO (są to kąty naprzemianległe utworzone przez przecięcie prostych równoległych AB i CD prostą BD).
- Boki:
  - |AB| = |CD| (przeciwległe boki równoległoboku są równe).
Krok 3: Przystawanie Trójkątów

Na podstawie cechy kąt-bok-kąt (KBK) możemy stwierdzić, że trójkąt AOB jest przystający do trójkąta COD (ΔAOB ≅ ΔCOD).

Krok 4: Wnioski z Przystawania

Skoro trójkąty AOB i COD są przystające, to odpowiadające im boki są równe. Zatem:

|AO| = |OC|
|BO| = |OD|

To dowodzi, że przekątne w równoległoboku dzielą się na połowy. Brawo! Udało się!

Przykład Zastosowania

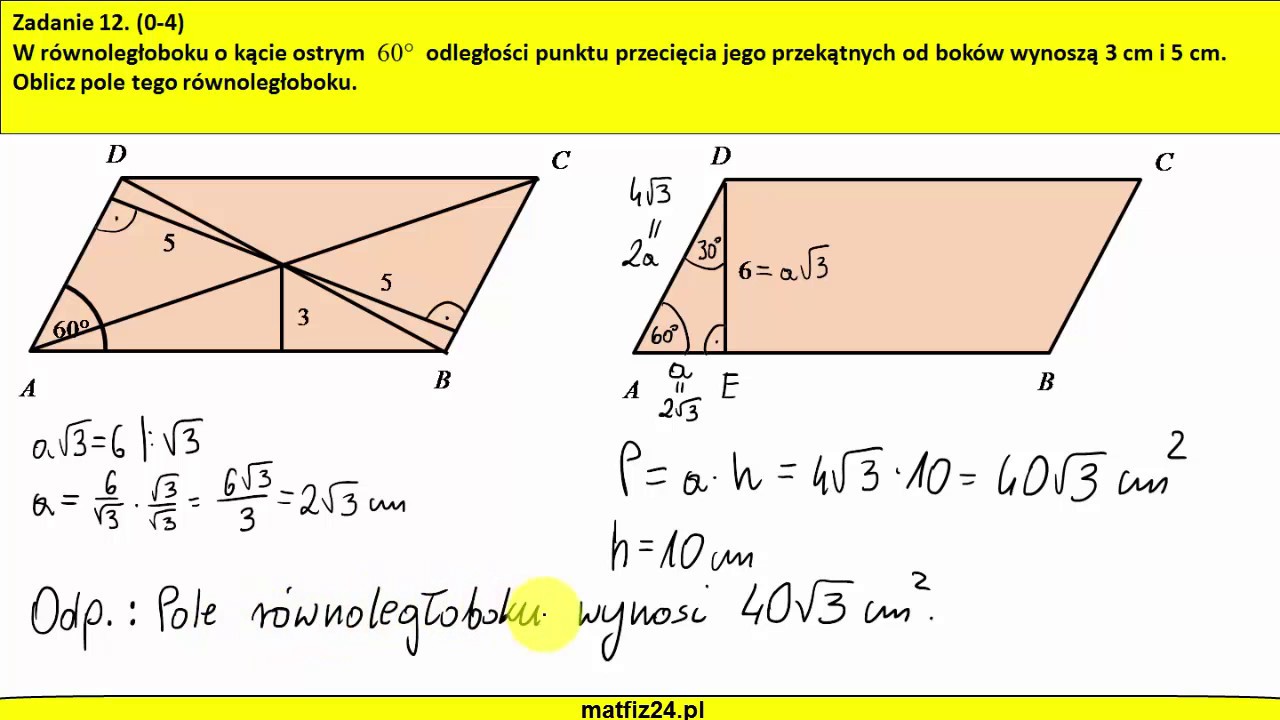
Załóżmy, że mamy równoległobok ABCD, w którym przekątna AC ma długość 10 cm, a przekątna BD ma długość 8 cm. Wiemy, że punkt O dzieli te przekątne na połowy.

|AO| = |OC| = 10 cm / 2 = 5 cm
|BO| = |OD| = 8 cm / 2 = 4 cm

To bardzo proste, prawda?

Kiedy Twierdzenie NIE Działa?

Pamiętajcie, że to twierdzenie dotyczy tylko równoległoboków. W innych czworokątach, takich jak trapezy (które nie są równoległobokami), przekątne zazwyczaj nie dzielą się na połowy. Należy być ostrożnym i nie stosować tego twierdzenia do czworokątów, o których nie wiemy na pewno, że są równoległobokami.

Typowe Zadania na Egzaminie

Na egzaminie możecie spodziewać się zadań, w których będziecie musieli:

Udowodnić, że dany czworokąt jest równoległobokiem (np. pokazując, że ma dwie pary boków równoległych).
Wykorzystać fakt, że przekątne dzielą się na połowy do obliczenia długości odcinków.
Zastosować twierdzenie w bardziej złożonych problemach geometrycznych.
Rozpoznać równoległobok na podstawie właściwości jego przekątnych.

Wskazówki i Triki

Rysujcie zawsze rysunki! Dobry rysunek to połowa sukcesu. Zaznaczcie na nim wszystko, co wiecie.
Pamiętajcie definicję równoległoboku. Zastanówcie się, które cechy równoległoboku mogą wam pomóc w rozwiązaniu zadania.
Szukajcie trójkątów przystających. Przystawanie trójkątów to bardzo często klucz do rozwiązania zadań geometrycznych.
Uważajcie na szczegóły. Czy na pewno dany czworokąt jest równoległobokiem? Czy na pewno kąty są naprzemianległe?

Podsumowanie i Powtórka

Powtórzmy najważniejsze informacje:

Równoległobok to czworokąt z dwiema parami boków równoległych i równych.
Przekątne w równoległoboku przecinają się w punkcie, który dzieli każdą z nich na połowy.
Dowód opiera się na przystawaniu trójkątów AOB i COD (cecha KBK).
To twierdzenie NIE działa w każdym czworokącie, tylko w równoległobokach (i ich szczególnych przypadkach).

Pamiętajcie, że geometria to przede wszystkim logiczne myślenie i umiejętność dostrzegania zależności. Im więcej ćwiczycie, tym lepiej będziecie rozumieć te zależności. Nie zrażajcie się trudnościami! Każdy błąd to okazja do nauki.

Powodzenia na sprawdzianie! Wierzę w Was! Ćwiczcie regularnie, róbcie rysunki, analizujcie dowody, a wszystko pójdzie dobrze. Pamiętajcie, że wiedza zdobyta podczas nauki geometrii przydaje się nie tylko na sprawdzianie, ale również w życiu codziennym, rozwijając logiczne myślenie i wyobraźnię przestrzenną. Trzymam kciuki!