Czy Przekątne Równoległoboku Przecinają Się W Połowie

Dzień dobry wszystkim! Dziś odpowiemy na bardzo ważne pytanie dotyczące równoległoboku: Czy przekątne równoległoboku przecinają się w połowie? Krótka odpowiedź brzmi: Tak! Ale zobaczmy to bliżej.
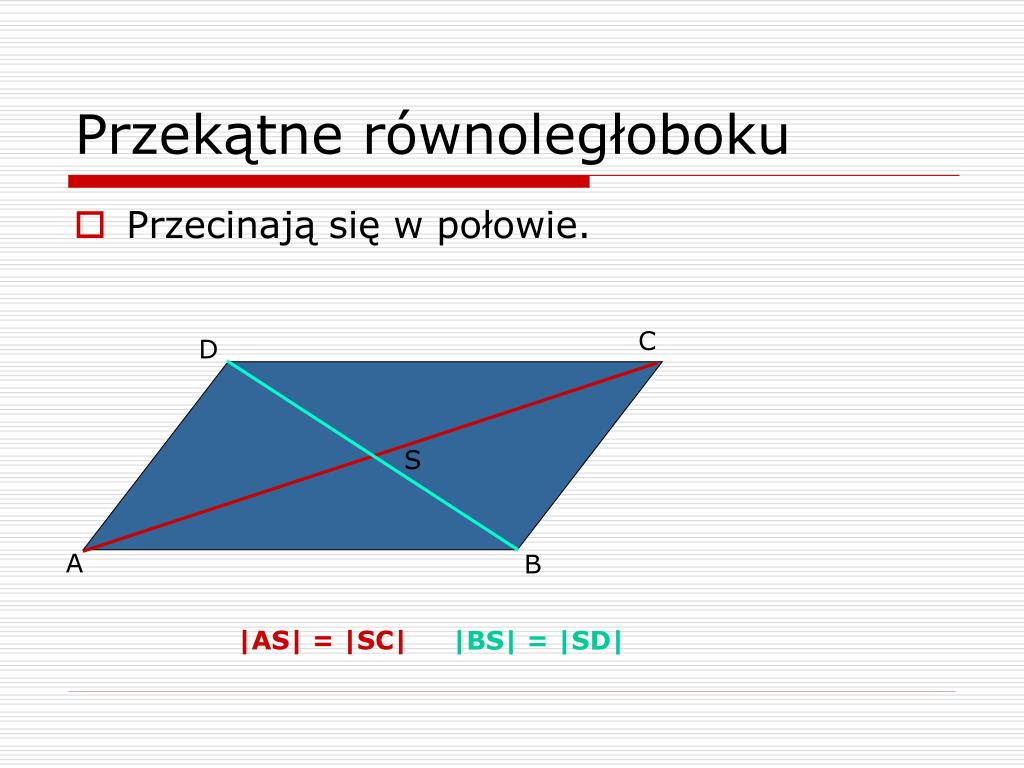
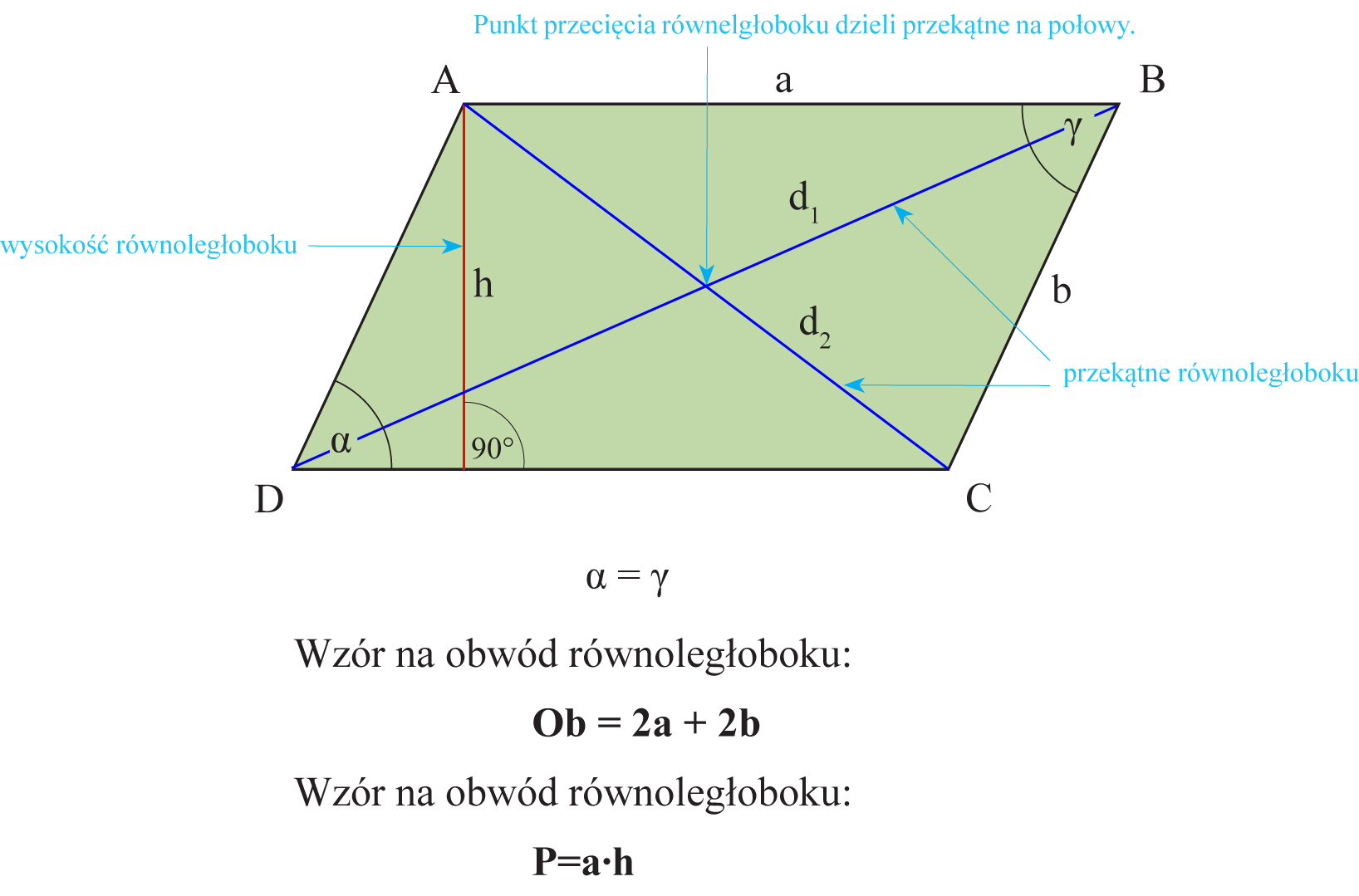
Wyobraźcie sobie równoległobok. To taki czworokąt, który ma dwie pary boków równoległych. Narysujcie go sobie na kartce! Teraz narysujcie przekątne. Przekątna to linia prosta, która łączy dwa wierzchołki, które nie są obok siebie. Zobaczycie, że te przekątne przetną się gdzieś w środku równoległoboku.
To właśnie ten punkt przecięcia jest bardzo ciekawy. Otóż, jeśli zmierzycie długość każdej z przekątnych, od wierzchołka do punktu przecięcia, zauważycie coś niezwykłego. Okaże się, że punkt przecięcia dzieli każdą z przekątnych na dwie równe części. Innymi słowy, punkt przecięcia jest dokładnie w połowie każdej z przekątnych.
To oznacza, że przekątne równoległoboku przecinają się w połowie. To ważna własność równoległoboku, która jest użyteczna w wielu zadaniach z geometrii.
Teraz rozważmy przykład. Załóżmy, że mamy równoległobok ABCD. Przekątne AC i BD przecinają się w punkcie O. Z tego, co już wiemy, wynika, że długość odcinka AO jest równa długości odcinka OC, a długość odcinka BO jest równa długości odcinka OD.
Spróbujmy to zwizualizować. Wyobraźcie sobie odcinek AC. Punkt O leży dokładnie po środku tego odcinka. Podobnie, punkt O leży dokładnie po środku odcinka BD. To jest właśnie sedno tego, że przekątne przecinają się w połowie.
To nie jest tylko ciekawostka. Ta własność ma bardzo praktyczne zastosowanie. Na przykład, jeśli znacie współrzędne wierzchołków równoległoboku, możecie łatwo znaleźć współrzędne punktu przecięcia przekątnych. Wystarczy obliczyć współrzędne środka odcinka dla jednej z przekątnych.
Podsumowując, przekątne równoległoboku zawsze przecinają się w połowie. Punkt przecięcia dzieli każdą z przekątnych na dwie równe części. Pamiętajcie o tym!
Dalsze przemyślenia
Można pomyśleć, co się stanie, jeśli równoległobok będzie miał specjalną formę. Na przykład, co się stanie, jeśli będzie to prostokąt? Albo romb? Albo kwadrat?
W przypadku prostokąta, przekątne również przecinają się w połowie, ponieważ prostokąt jest szczególnym przypadkiem równoległoboku. Co więcej, w prostokącie przekątne mają równe długości.
W przypadku rombu, przekątne również przecinają się w połowie, ponieważ romb jest również szczególnym przypadkiem równoległoboku. Dodatkowo, w rombie przekątne przecinają się pod kątem prostym.
W przypadku kwadratu, który jest zarówno prostokątem, jak i rombem, przekątne również przecinają się w połowie, mają równe długości i przecinają się pod kątem prostym.
Widzicie więc, że własność przecinania się przekątnych w połowie jest charakterystyczna dla wszystkich równoległoboków, niezależnie od tego, czy są to prostokąty, romby czy kwadraty.
Teraz spróbujmy rozwiązać proste zadanie. Mamy równoległobok ABCD. Punkt O jest punktem przecięcia przekątnych AC i BD. Wiemy, że AO = 5 cm. Ile wynosi długość odcinka AC?
Ponieważ wiemy, że przekątne przecinają się w połowie, to AO = OC. Zatem OC = 5 cm. Długość odcinka AC jest równa sumie długości odcinków AO i OC, czyli AC = AO + OC = 5 cm + 5 cm = 10 cm. Odpowiedź: długość odcinka AC wynosi 10 cm.
Mam nadzieję, że teraz lepiej rozumiecie, dlaczego przekątne równoległoboku przecinają się w połowie i jak można tę własność wykorzystać w praktyce. Pamiętajcie o tym, rozwiązując zadania z geometrii!
Spróbujcie teraz sami rozwiązać kilka podobnych zadań. To najlepszy sposób, aby utrwalić swoją wiedzę. Na przykład, spróbujcie znaleźć współrzędne punktu przecięcia przekątnych, jeśli znacie współrzędne wierzchołków równoległoboku. Albo spróbujcie obliczyć długość przekątnej, jeśli znacie długość jednego z odcinków, na które dzieli ją punkt przecięcia.
Nie bójcie się eksperymentować i szukać różnych rozwiązań. Geometria to fascynująca dziedzina, która rozwija logiczne myślenie i umiejętność rozwiązywania problemów.
Ćwiczenia
Zróbmy jeszcze jedno ćwiczenie, żeby dobrze utrwalić wiedzę. Mamy równoległobok EFGH. Przekątne EG i FH przecinają się w punkcie P. Wiemy, że FP = 3x + 2 i PH = 5x - 4. Ile wynosi długość odcinka FH?
Ponieważ przekątne przecinają się w połowie, to FP = PH. Zatem 3x + 2 = 5x - 4. Teraz rozwiążmy to równanie:
5x - 3x = 2 + 4 2x = 6 x = 3
Teraz, gdy znamy wartość x, możemy obliczyć długość odcinka FP:
FP = 3x + 2 = 3 * 3 + 2 = 9 + 2 = 11
Ponieważ FP = PH, to PH = 11.
Długość odcinka FH jest równa sumie długości odcinków FP i PH:
FH = FP + PH = 11 + 11 = 22
Odpowiedź: długość odcinka FH wynosi 22.
To zadanie pokazało, jak wykorzystać własność przecinania się przekątnych w połowie do rozwiązywania równań i obliczania długości odcinków.
Podsumowanie
Mam nadzieję, że po tych przykładach i ćwiczeniach macie już pełne zrozumienie tego, dlaczego przekątne równoległoboku przecinają się w połowie. Pamiętajcie, że ta własność jest bardzo ważna i przydatna w wielu zadaniach z geometrii. Używajcie jej śmiało i nie bójcie się rozwiązywać trudnych problemów.
Pamiętajcie o regularnych ćwiczeniach. Im więcej zadań rozwiążecie, tym lepiej zrozumiecie geometrię i tym łatwiej będziecie radzić sobie z trudnymi zagadnieniami. Powodzenia!