Czy Pierwiastki To Liczby Wymierne

Czy kiedykolwiek zastanawiałeś się nad tym, jakie liczby kryją się pod symbolem pierwiastka? Może miałeś wrażenie, że to jakaś skomplikowana, tajemnicza kategoria matematyczna, oderwana od tych "normalnych" liczb, których używamy na co dzień. Zrozumienie, czy pierwiastki są liczbami wymiernymi, czy nie, to klucz do głębszego zrozumienia świata liczb. Spróbujmy to razem rozwikłać, bez zbędnego komplikowania. Pokażę Ci, jak do tego podejść krok po kroku.

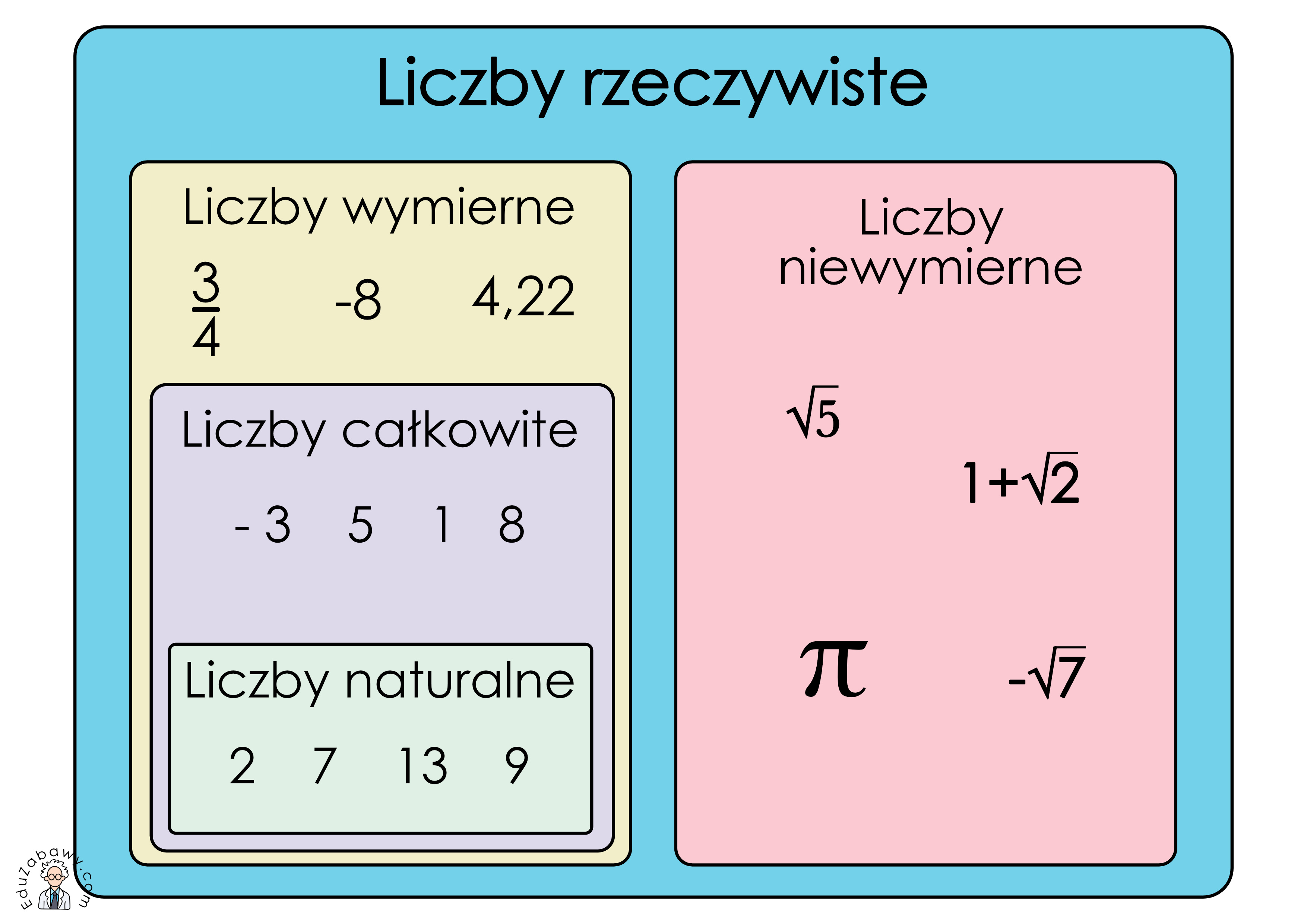
Czym są liczby wymierne?

Zacznijmy od podstaw. Liczby wymierne to takie liczby, które można zapisać w postaci ułamka zwykłego p/q, gdzie p i q są liczbami całkowitymi, a q jest różne od zera. Innymi słowy, jeśli możesz jakąś liczbę przedstawić jako iloraz dwóch liczb całkowitych, to ta liczba jest wymierna. Przykłady liczb wymiernych to: 1/2, -3/4, 5, 0, 1.75 (bo można to zapisać jako 7/4). Wszystkie liczby całkowite są liczbami wymiernymi, ponieważ można je zapisać jako ułamek z mianownikiem równym 1 (np. 5 = 5/1).

Kluczowa cecha liczb wymiernych to fakt, że ich rozwinięcie dziesiętne jest albo skończone, albo nieskończone okresowe. Na przykład, 1/4 = 0.25 (rozwinięcie skończone), a 1/3 = 0.(3) (rozwinięcie nieskończone okresowe, gdzie 3 powtarza się w nieskończoność).

Czym są pierwiastki?

Pierwiastek kwadratowy z liczby x to taka liczba, która pomnożona przez samą siebie daje x. Oznaczamy go symbolem √x. Na przykład, pierwiastek kwadratowy z 9 to 3 (√9 = 3), bo 3 * 3 = 9. Podobnie, pierwiastek kwadratowy z 16 to 4 (√16 = 4), bo 4 * 4 = 16. Istnieją również pierwiastki wyższych stopni, np. pierwiastek trzeciego stopnia (sześcienny) oznaczany jako ∛x. ∛8 = 2, bo 2 * 2 * 2 = 8.

Ważne! Zastanówmy się nad pierwiastkami liczb ujemnych. W zbiorze liczb rzeczywistych, pierwiastki kwadratowe z liczb ujemnych nie istnieją (nie ma takiej liczby rzeczywistej, która podniesiona do kwadratu dałaby liczbę ujemną). Dlatego, mówiąc o pierwiastkach, zazwyczaj mamy na myśli pierwiastki z liczb nieujemnych.

Czy wszystkie pierwiastki są liczbami wymiernymi?

I tu dochodzimy do sedna pytania. Odpowiedź brzmi: NIE. Nie wszystkie pierwiastki są liczbami wymiernymi. Niektóre pierwiastki są liczbami niewymiernymi. A co to oznacza?

Liczba niewymierna to taka liczba, której nie można zapisać w postaci ułamka p/q, gdzie p i q są liczbami całkowitymi. Ich rozwinięcie dziesiętne jest nieskończone i nieokresowe. Oznacza to, że cyfry po przecinku nigdy się nie powtarzają w regularny sposób.

Najbardziej znanym przykładem liczby niewymiernej jest √2 (pierwiastek kwadratowy z 2). Jego rozwinięcie dziesiętne to w przybliżeniu 1.41421356… i ciągnie się w nieskończoność bez żadnego powtarzającego się wzoru. Dowód na to, że √2 jest liczbą niewymierną, jest jednym z klasycznych dowodów w matematyce.

Dlaczego niektóre pierwiastki są niewymierne?

To wynika z natury niektórych liczb. Jeśli liczba podpierwiastkowa (czyli liczba, z której wyciągamy pierwiastek) nie jest kwadratem (lub sześcianem, itd.) liczby całkowitej, to jej pierwiastek będzie liczbą niewymierną. Na przykład:

√4 = 2 (wymierna, bo 4 jest kwadratem liczby 2)
√9 = 3 (wymierna, bo 9 jest kwadratem liczby 3)
√16 = 4 (wymierna, bo 16 jest kwadratem liczby 4)
√25 = 5 (wymierna, bo 25 jest kwadratem liczby 5)

Ale:

√2 = 1.41421356… (niewymierna)
√3 = 1.7320508… (niewymierna)
√5 = 2.2360679… (niewymierna)
√7 = 2.6457513… (niewymierna)

Krótko mówiąc: Jeśli liczba podpierwiastkowa nie jest "idealnym kwadratem" (lub "idealnym sześcianem" dla pierwiastków trzeciego stopnia itd.), to pierwiastek z niej jest liczbą niewymierną.

Przykłady i zastosowania

Liczby niewymierne, a w szczególności pierwiastki, mają szerokie zastosowanie w matematyce, fizyce, inżynierii i informatyce.

Geometria: Długość przekątnej kwadratu o boku 1 wynosi √2.
Trygonometria: Wartości funkcji trygonometrycznych dla niektórych kątów (np. sin 45°) zawierają pierwiastki.
Fizyka: Wzory opisujące ruch wahadła, prędkość dźwięku i wiele innych zjawisk fizycznych często zawierają pierwiastki.

Praktyczny przykład: Wyobraź sobie, że projektujesz budynek i potrzebujesz obliczyć długość przekątnej prostokątnej działki. Jeśli boki działki mają długości, powiedzmy, 3 metry i 4 metry, to długość przekątnej, zgodnie z twierdzeniem Pitagorasa, wyniesie √(3² + 4²) = √25 = 5 metrów (liczba wymierna). Ale gdyby boki miały długości 1 metr i 1 metr, to przekątna miałaby długość √(1² + 1²) = √2 metra (liczba niewymierna).

Podsumowanie

Zapamiętaj:

Liczby wymierne można zapisać jako ułamek p/q, gdzie p i q są liczbami całkowitymi. Mają rozwinięcie dziesiętne skończone lub nieskończone okresowe.
Liczby niewymierne nie można zapisać jako ułamka p/q. Mają rozwinięcie dziesiętne nieskończone i nieokresowe.
Nie wszystkie pierwiastki są liczbami wymiernymi.
Pierwiastki z liczb, które nie są "idealnymi kwadratami" (lub "idealnymi sześcianami" itd.), są liczbami niewymiernymi.

Zrozumienie różnicy między liczbami wymiernymi i niewymiernymi, w tym pierwiastkami, to kluczowy krok w dalszej edukacji matematycznej. Dzięki temu łatwiej zrozumiesz bardziej zaawansowane koncepcje i zastosowania matematyki w różnych dziedzinach życia.

Co dalej?

Jeżeli zainteresował Cię ten temat, możesz poszukać więcej informacji o:

Dowodach na niewymierność pierwiastka z 2.
Innych przykładach liczb niewymiernych (np. liczbie π, liczbie e).
Operacjach na liczbach wymiernych i niewymiernych.

Mam nadzieję, że ten artykuł pomógł Ci zrozumieć, czym są liczby wymierne i niewymierne, oraz odpowiedział na pytanie, czy pierwiastki są liczbami wymiernymi. Powodzenia w dalszej nauce matematyki!