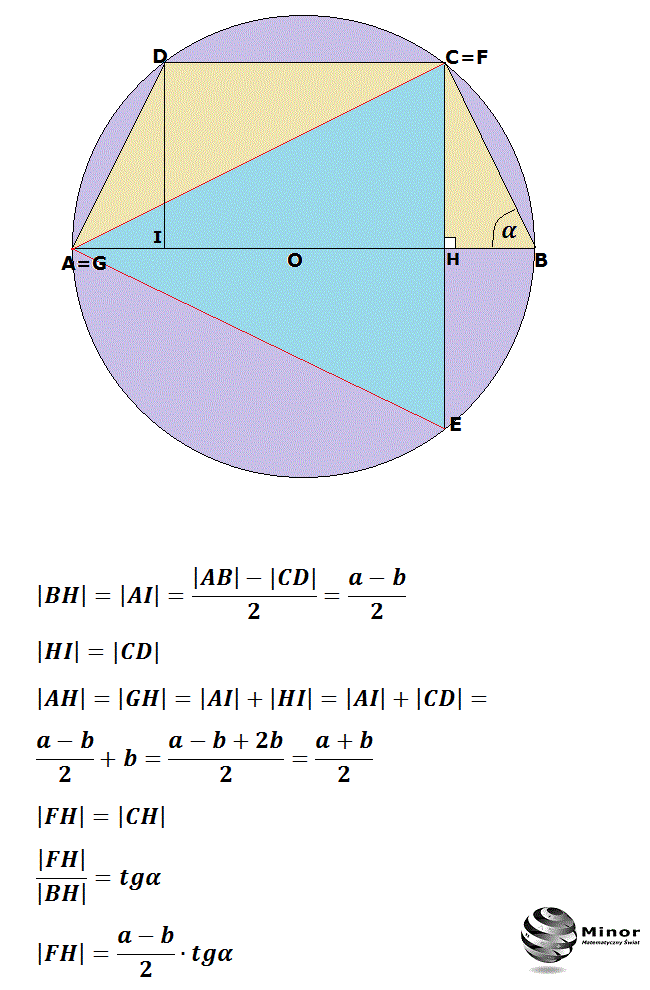Czy Każdy Trapez Wpisany W Okrąg Jest Równoramienny

Zastanawialiście się kiedyś, co łączy trapez i okrąg? Albo czy każdy trapez, który "mieści się" w okręgu, musi być jakiś specjalny? Spróbujmy to rozgryźć razem, krok po kroku, żebyście zrozumieli to bez problemu. Nie martwcie się skomplikowanymi wzorami, postaramy się to wszystko wytłumaczyć prosto i zrozumiale.

Trapez – co to takiego?

Zacznijmy od podstaw. Trapez to czworokąt, który ma co najmniej jedną parę boków równoległych. Te boki równoległe nazywamy podstawami trapezu, a pozostałe dwa to ramiona. Wyobraźcie sobie, że macie stół, który z jednej strony jest szerszy niż z drugiej, a boki go łączące nie są równoległe – to właśnie trapez!

Mamy różne rodzaje trapezów. Najprostszy to trapez, w którym boki nierównoległe (ramiona) mają różne długości. Ale jest też taki "specjalny" trapez, który nazywamy równoramiennym.

Trapez Równoramienny – czym się charakteryzuje?

Trapez równoramienny to taki trapez, którego ramiona (czyli boki nierównoległe) mają taką samą długość. To jakby stół, o którym wspominaliśmy wcześniej, tylko że te boki łączące podstawy są dokładnie takie same. Oprócz równych ramion, trapez równoramienny ma jeszcze jedną fajną cechę: kąty przy każdej z podstaw są równe. Oznacza to, że kąt ostry przy dolnej podstawie jest taki sam jak drugi kąt ostry przy dolnej podstawie, a kąt rozwarty przy górnej podstawie jest taki sam jak drugi kąt rozwarty przy górnej podstawie.

Okrąg – nasz "domek" dla trapezu

Okrąg to zbiór wszystkich punktów na płaszczyźnie, które znajdują się w równej odległości od jednego punktu, nazywanego środkiem okręgu. Wyobraźcie sobie, że macie sznurek, przywiązujecie go do jednego punktu na kartce, a potem naciągacie sznurek i rysujecie okrąg, trzymając sznurek cały czas napięty. To właśnie okrąg!

Trapez Wpisany w Okrąg – co to znaczy?

Teraz dochodzimy do sedna sprawy. Trapez wpisany w okrąg to taki trapez, którego wszystkie wierzchołki (czyli rogi) leżą na okręgu. Inaczej mówiąc, okrąg przechodzi przez każdy wierzchołek trapezu. Wyobraźcie sobie, że rysujecie okrąg, a potem w tym okręgu rysujecie trapez, tak żeby wszystkie cztery rogi trapezu "dotykały" okręgu.

##Czy Każdy Trapez Wpisany w Okrąg Jest Równoramienny?

I teraz pytanie za milion punktów: czy każdy trapez, który "mieści się" w okręgu (czyli jest wpisany w okrąg), musi być równoramienny? Odpowiedź brzmi: tak! Ale dlaczego? Spróbujmy to zrozumieć.

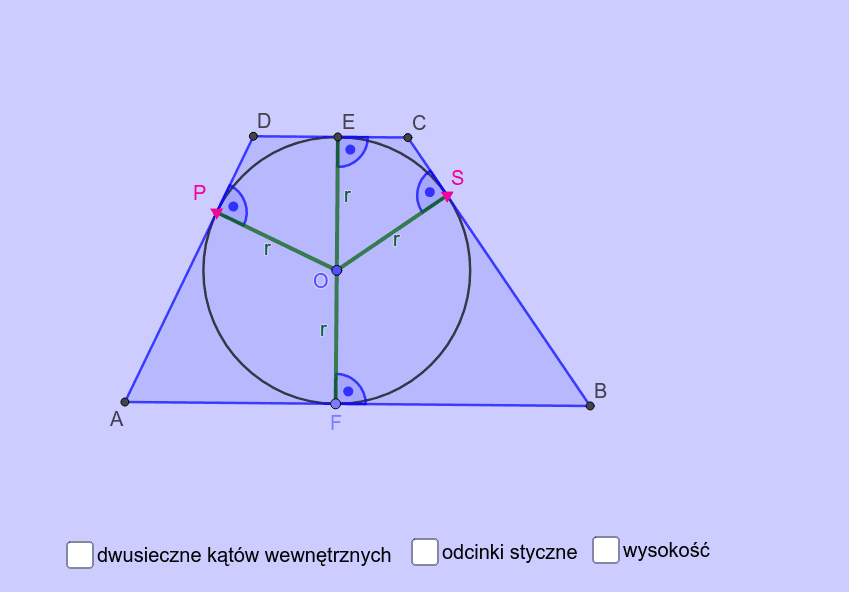
Kluczem jest twierdzenie o czworokącie wpisanym w okrąg. Twierdzenie to mówi, że czworokąt (czyli figura mająca cztery boki) można wpisać w okrąg wtedy i tylko wtedy, gdy suma miar przeciwległych kątów tego czworokąta wynosi 180 stopni.

Czyli, jeśli mamy trapez wpisany w okrąg, to suma miar jego kątów przy jednej z ramion (czyli tych boków nierównoległych) wynosi 180 stopni. Wiemy też, że w trapezie kąty przy jednym ramieniu sumują się do 180 stopni (to wynika z tego, że podstawy są równoległe).

Spróbujmy to zapisać: niech α i β będą kątami przy jednym ramieniu trapezu, a γ i δ kątami przy drugim ramieniu. Ponieważ trapez jest wpisany w okrąg, to:

• α + γ = 180 stopni
• β + δ = 180 stopni

Dodatkowo, w trapezie:

• α + β = 180 stopni
• γ + δ = 180 stopni

Z tych równań wynika, że α = δ oraz β = γ.

Teraz wyobraźcie sobie, że dorysowujemy do trapezu równoramiennego prostokąt, tak żeby powstał trójkąt równoramienny. Z własności trójkąta równoramiennego i prostokąta łatwo wywnioskować, że kąty przy podstawie są równe. Te kąty to właśnie nasze α i δ, oraz β i γ.

Ponieważ kąty przy podstawie trapezu są równe (α=δ oraz β=γ), a ramię trapezu łączy te podstawy, to to ramie musi być tak ustawione, by "równoważyć" te kąty. Jeśli ramiona miałyby różne długości, to niemożliwe byłoby, żeby kąty przy podstawie były równe.

Dowód Geometryczny (Alternatywny, Bardziej Wizualny)

Można to też pokazać bardziej wizualnie. Narysujcie okrąg. Następnie narysujcie dwie równoległe cięciwy (odcinki łączące dwa punkty na okręgu), które będą podstawami trapezu. Załóżmy, że ramiona tego trapezu nie są równe. Zauważcie, że jeśli przesuwacie jeden z końców krótszego ramienia po okręgu, aby je wydłużyć, to drugi koniec tego ramienia również musi się przesunąć. Żeby suma kątów przeciwległych pozostała stała (180 stopni), zmiana położenia jednego wierzchołka wpływa na pozostałe. Jedynym sposobem na zachowanie tej zależności i równoległości podstaw jest, aby ramiona były symetryczne względem osi okręgu przechodzącej przez środek podstaw. Taka symetria implikuje, że ramiona mają równe długości.

Podsumowanie

Podsumowując: każdy trapez, który można wpisać w okrąg, musi być trapezem równoramiennym. Wynika to z twierdzenia o czworokątach wpisanych w okrąg i własności trapezów. To ciekawe połączenie geometrii! Mam nadzieję, że teraz rozumiecie to zagadnienie. Pamiętajcie, żeby w razie wątpliwości narysować sobie to wszystko na kartce – wtedy wszystko staje się bardziej jasne.