Czy Każdy Romb Jest Trapezem
Zapewne, zastanawiając się nad geometrią i własnościami różnych figur, natknąłeś się na pytanie, które często pojawia się w dyskusjach: "Czy każdy romb jest trapezem?". Z pozoru proste pytanie, kryje w sobie subtelności, które warto zgłębić. Rozumiem twoje potencjalne zakłopotanie. Geometria, z jej aksjomatami i definicjami, potrafi być trudna do ogarnięcia. Celem tego artykułu jest rozjaśnienie tej kwestii, używając prostych przykładów i objaśnień, abyś mógł w pełni zrozumieć relację między rombem a trapezem.
Romb i Trapez: Definicje i Podstawowe Własności
Zanim przejdziemy do sedna sprawy, odświeżmy definicje tych dwóch figur geometrycznych. Pamiętajmy, że precyzyjne zrozumienie definicji jest kluczowe do rozwiązywania problemów geometrycznych.
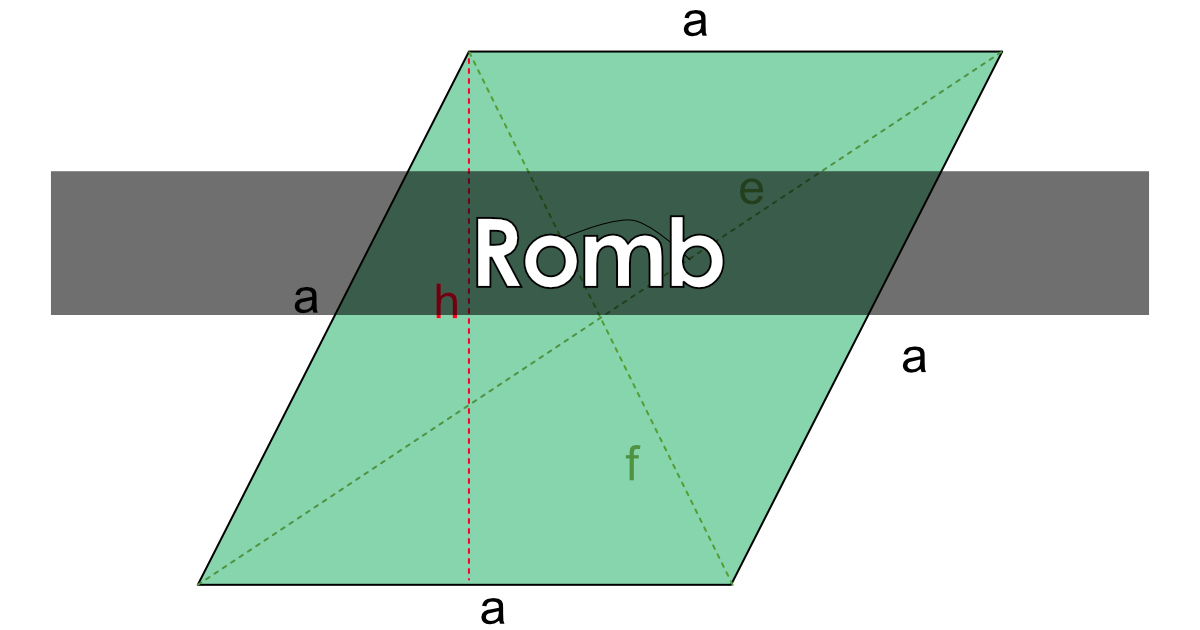
Romb
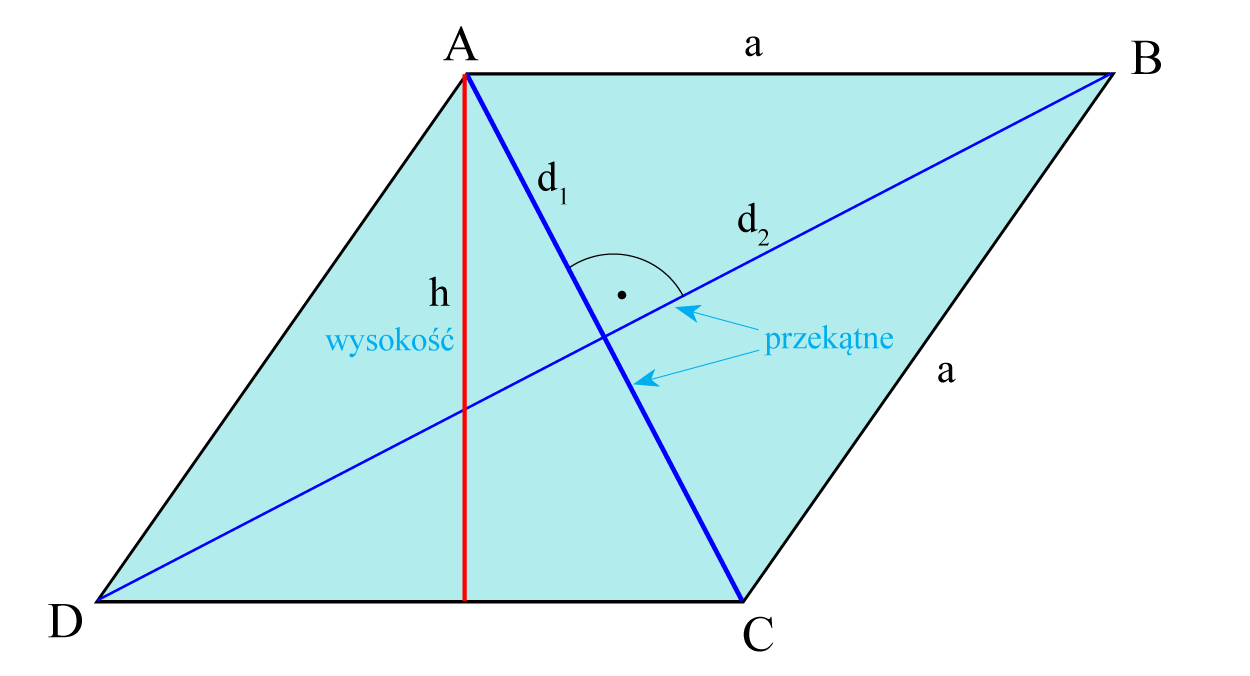
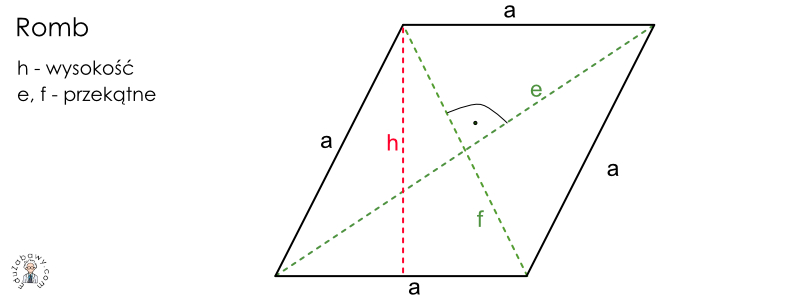
Romb to czworokąt, który ma wszystkie boki równe. Dodatkowo, posiada następujące własności:
- Przeciwległe kąty są równe.
- Przekątne przecinają się pod kątem prostym i dzielą się na połowy.
- Przekątne są dwusiecznymi kątów rombu.
Wyobraź sobie latawiec. Romb jest trochę jak latawiec, tylko jeszcze bardziej symetryczny – wszystkie boki są tej samej długości.
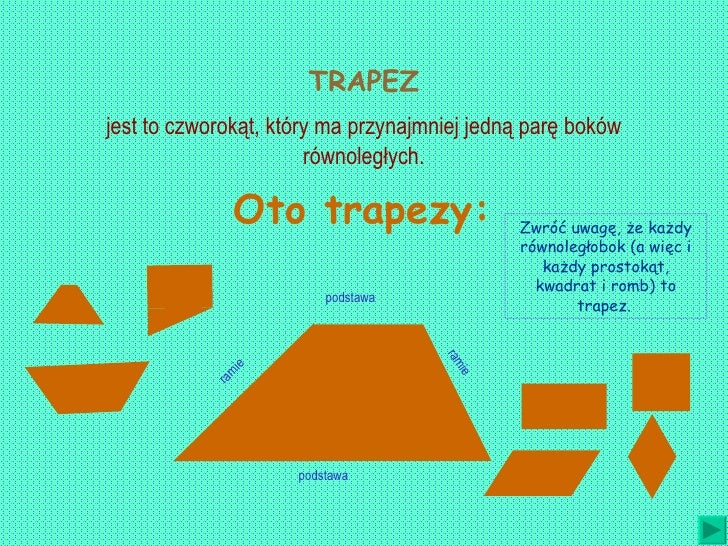
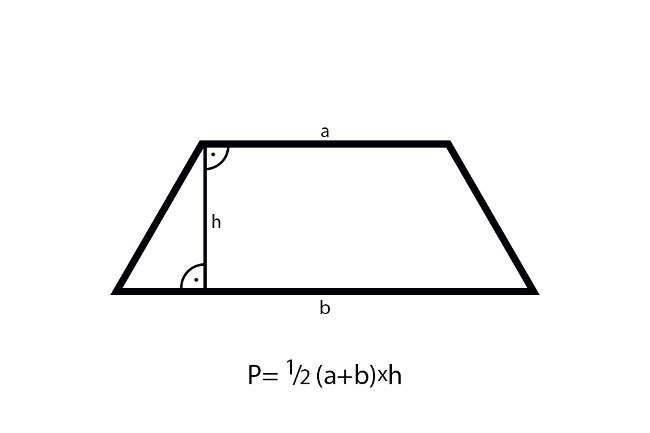
Trapez
Trapez to czworokąt, który ma przynajmniej jedną parę boków równoległych. Te równoległe boki nazywamy podstawami trapezu, a pozostałe dwa – ramionami.
Istnieją różne rodzaje trapezów:
- Trapez równoramienny: Ma ramiona równej długości.
- Trapez prostokątny: Ma co najmniej jeden kąt prosty.
Pomyśl o blacie stołu, który jest szerszy z jednej strony niż z drugiej – często to trapez. Najważniejsze, żeby miał dwie równoległe krawędzie.
Czy Romb Spełnia Warunki Trapezu?
Kluczem do odpowiedzi na pytanie, czy romb jest trapezem, jest zrozumienie definicji trapezu. Trapez musi mieć przynajmniej jedną parę boków równoległych. A co z rombem?
W rombie, przeciwległe boki są równoległe. To wynika z jego definicji i właściwości. Skoro romb ma dwie pary boków równoległych, to z pewnością spełnia warunek trapezu, który wymaga tylko jednej pary boków równoległych.
Zatem, każdy romb jest trapezem. Można to powiedzieć inaczej: zbiór rombów jest podzbiorem zbioru trapezów.
Potencjalne Kontrargumenty i Dlaczego Są Błędne
Często pojawiają się wątpliwości, ponieważ intuicyjnie myślimy o trapezie jako o figurze "nierównomiernej", gdzie tylko jedna para boków jest równoległa, a ramiona są różne. Myślimy o nim jako o czymś mniej regularnym niż romb.
Niektórzy mogą argumentować, że trapez "typowo" ma tylko jedną parę boków równoległych. To prawda, ale definicja trapezu nie wyklucza posiadania dwóch par boków równoległych. Definicja jest inkluzywna, a nie ekskluzywna.
Pomyśl o tym tak: czy kwadrat jest prostokątem? Tak, jest. Kwadrat spełnia wszystkie warunki prostokąta (cztery kąty proste), a dodatkowo ma wszystkie boki równe. Podobnie, romb spełnia warunki trapezu (przynajmniej jedna para boków równoległych), a dodatkowo ma wszystkie boki równe.
Realny Wpływ i Zastosowanie
Zrozumienie relacji między figurami geometrycznymi, takimi jak romb i trapez, nie jest tylko akademicką ciekawostką. Ma to realny wpływ na:
- Rozwiązywanie problemów geometrycznych: Wiedza ta pozwala na korzystanie z właściwości trapezu przy rozwiązywaniu zadań dotyczących rombu i odwrotnie.
- Projektowanie i inżynieria: W architekturze i inżynierii często wykorzystuje się różne kształty, a znajomość ich właściwości pozwala na optymalizację konstrukcji.
- Grafika komputerowa i gry: Algorytmy graficzne wykorzystują wiedzę o figurach geometrycznych do renderowania obiektów wirtualnych.
- Edukacja: Ułatwia zrozumienie bardziej złożonych koncepcji matematycznych.
Wyobraź sobie architekta projektującego dach. Wiedza, że romb jest rodzajem trapezu, może pomóc mu w optymalnym doborze materiałów i kątów nachylenia, aby zapewnić stabilność i estetykę konstrukcji.
Proste Przykłady dla Lepszego Zrozumienia
Spróbujmy podejść do tego jeszcze inaczej. Załóżmy, że masz pudełko kredek. W tym pudełku są kredki czerwone i kredki niebieskie. Czy każda czerwona kredka jest kredką? Oczywiście! Podobnie, każdy romb jest trapezem. Romb jest szczególnym przypadkiem trapezu.
Inny przykład: Każdy pies jest ssakiem. Czy to oznacza, że każdy ssak jest psem? Nie. Podobnie, każdy romb jest trapezem, ale nie każdy trapez jest rombem.
Rozwiązania i Kolejne Kroki
Jeśli nadal masz wątpliwości, polecam:
- Narysowanie różnych rombów i trapezów: Zauważ, że romb zawsze spełnia definicję trapezu.
- Ponowne przeczytanie definicji: Skup się na słowach "przynajmniej" i "co najmniej" w definicji trapezu.
- Rozwiązanie kilku zadań geometrycznych: Spróbuj zastosować wiedzę o relacji między rombem a trapezem w praktyce.
- Dyskutowanie z innymi: Porozmawiaj o tym z kolegami, nauczycielem matematyki, lub na forach internetowych. Wymiana myśli pomoże ci utrwalić wiedzę.
Pamiętaj, że zrozumienie matematyki to proces. Nie zrażaj się, jeśli nie wszystko od razu jest jasne. Ważne jest, aby zadawać pytania i szukać odpowiedzi.
Podsumowanie
Podsumowując, odpowiedź brzmi tak: każdy romb jest trapezem. Wynika to z definicji trapezu, która wymaga posiadania co najmniej jednej pary boków równoległych, a romb ma dwie pary boków równoległych.
Mam nadzieję, że ten artykuł pomógł ci zrozumieć tę kwestię. Geometria może być fascynująca, gdy ją dobrze zrozumiesz. Wiedza ta otwiera drzwi do rozwiązywania problemów i lepszego zrozumienia otaczającego nas świata.
Czy po przeczytaniu tego artykułu czujesz się pewniej w rozróżnianiu rombów i trapezów oraz w zrozumieniu ich wzajemnych relacji? A może masz jeszcze jakieś pytania, na które chciałbyś uzyskać odpowiedź?