Czy Każdy Kwadrat Jest Rombem

Czy zastanawiałeś się kiedyś, jak powiązane są ze sobą różne figury geometryczne? Czy kwadrat jest po prostu szczególnym przypadkiem rombu, czy też są to zupełnie odrębne byty? W tym artykule dokładnie przyjrzymy się tej kwestii, rozstrzygając wszelkie wątpliwości i analizując definicje tych figur. Skierowany jest on do wszystkich osób zainteresowanych matematyką, uczniów i studentów, a także do każdego, kto chciałby odświeżyć swoją wiedzę z zakresu geometrii.
Definicje: Podstawy, które musimy znać
Zanim przejdziemy do sedna sprawy, musimy solidnie zdefiniować oba pojęcia: kwadrat i romb. To klucz do zrozumienia relacji między nimi.
Czym jest romb?
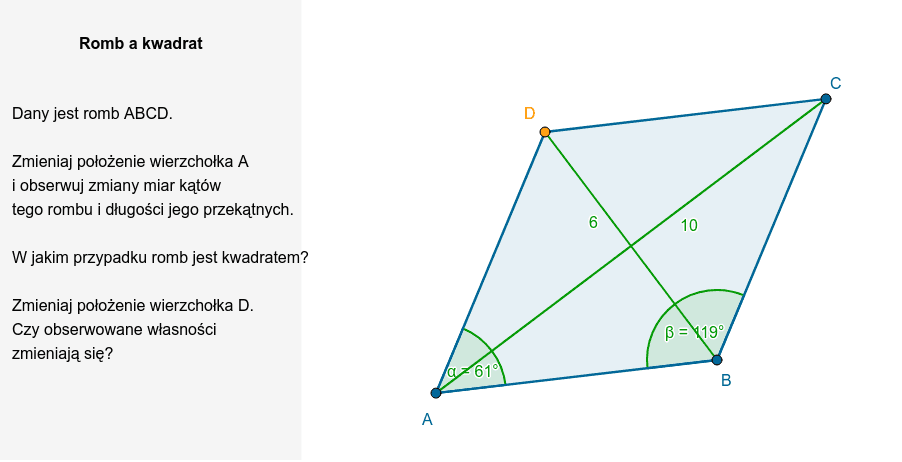
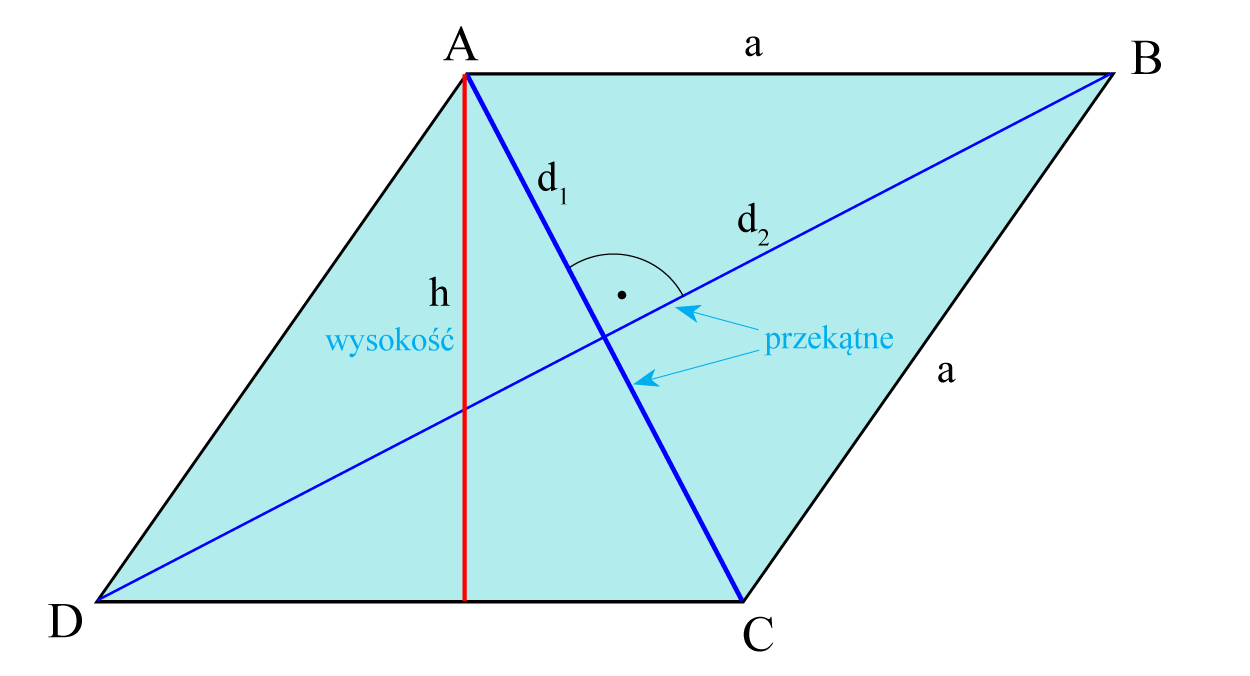
Romb to czworokąt, który posiada następujące cechy:
- Wszystkie cztery boki są równej długości.
- Przeciwległe kąty są równe.
- Przekątne przecinają się pod kątem prostym.
- Przekątne dzielą się na połowy w punkcie przecięcia.
Ważne: Romb nie musi mieć kątów prostych. To właśnie odróżnia go od kwadratu.
Czym jest kwadrat?
Kwadrat to czworokąt, który charakteryzuje się:
- Wszystkie cztery boki są równej długości.
- Wszystkie cztery kąty są proste (90 stopni).
- Przekątne są równej długości.
- Przekątne przecinają się pod kątem prostym.
- Przekątne dzielą się na połowy w punkcie przecięcia.
Kwadrat to figura, która łączy w sobie cechy prostokąta (wszystkie kąty proste) i rombu (wszystkie boki równe).
Analiza: Kwadrat jako szczególny przypadek rombu
Teraz, gdy mamy już jasne definicje, możemy przystąpić do analizy. Czy kwadrat spełnia wszystkie warunki definicji rombu? Sprawdźmy:
- Czy kwadrat ma wszystkie boki równej długości? Tak.
- Czy kwadrat ma przeciwległe kąty równe? Tak, ponieważ wszystkie kąty są proste (90 stopni).
- Czy przekątne kwadratu przecinają się pod kątem prostym? Tak.
- Czy przekątne kwadratu dzielą się na połowy w punkcie przecięcia? Tak.
Jak widzimy, kwadrat spełnia wszystkie kryteria definicji rombu. Dodatkowo, kwadrat ma jeszcze jedną cechę, której romb nie musi mieć: wszystkie kąty proste.
Odpowiedź: Tak, kwadrat jest rombem!
Na podstawie powyższej analizy, możemy śmiało stwierdzić: każdy kwadrat jest rombem. Kwadrat jest po prostu szczególnym przypadkiem rombu, takim, który posiada dodatkową właściwość – wszystkie kąty proste.
Można to porównać do relacji między owocami. Każda jabłoń rodzi owoce, które nazywamy jabłkami. Każde jabłko jest owocem, ale nie każdy owoc jest jabłkiem. Podobnie, każdy kwadrat jest rombem, ale nie każdy romb jest kwadratem.
Przykłady i wizualizacje
Wyobraź sobie romb. Możesz go trochę "przechylić" na boki. Jeśli przechylasz go tak, aby wszystkie kąty stały się proste, to otrzymasz kwadrat. Kwadrat to po prostu "wyprostowany" romb!
Można też spojrzeć na to w kategoriach diagramów Venna. Zbiór rombów jest większy, a zbiór kwadratów znajduje się wewnątrz zbioru rombów. Oznacza to, że każdy element ze zbioru kwadratów (czyli każdy kwadrat) należy również do zbioru rombów.
Dlaczego to jest ważne?
Zrozumienie relacji między różnymi figurami geometrycznymi jest bardzo ważne w matematyce. Pozwala to na:
- Upraszczanie dowodów: Jeśli udowodnimy coś dla rombu, to automatycznie wiemy, że jest to prawdziwe dla kwadratu.
- Rozwiązywanie zadań: Znając cechy rombu, możemy wykorzystać je do rozwiązywania problemów związanych z kwadratami.
- Głębsze zrozumienie geometrii: Poznawanie powiązań między różnymi pojęciami matematycznymi pomaga w budowaniu solidnej bazy wiedzy.
Ponadto, zrozumienie tych relacji kształtuje umiejętność logicznego myślenia i dedukcji, co jest cenne nie tylko w matematyce, ale i w życiu codziennym.
Częste błędy i nieporozumienia
Częstym błędem jest myślenie, że romb *musi* mieć kąty ostre i rozwarte. Romb **może** mieć kąty ostre i rozwarte, ale nie musi. Kwadrat jest tego najlepszym przykładem – jest rombem, który ma same kąty proste.
Innym błędem jest postrzeganie kwadratu i rombu jako zupełnie oddzielnych figur. Należy pamiętać, że kwadrat to po prostu szczególny przypadek rombu, który spełnia dodatkowy warunek.
Podsumowanie i wnioski
Mam nadzieję, że ten artykuł pomógł Ci zrozumieć, że każdy kwadrat jest rombem. Kwadrat to po prostu "wypasiony" romb, który ma wszystkie kąty proste. Zapamiętaj to i wykorzystuj tę wiedzę w rozwiązywaniu zadań i w dalszej nauce geometrii!
Geometria jest fascynująca, a zrozumienie relacji między różnymi figurami otwiera drzwi do głębszego poznawania matematyki. Nie bój się zadawać pytań i eksplorować – świat geometrii czeka na odkrycie!
Teraz, gdy wiesz, że każdy kwadrat jest rombem, możesz spróbować rozwiązać kilka zadań, wykorzystując tę wiedzę. Powodzenia!