Czy Każdy Kwadrat Jest Prostokątem

Zapewne nieraz słyszałeś to pytanie, być może sam je zadawałeś: Czy każdy kwadrat jest prostokątem? To pytanie, które wydaje się proste, ale potrafi wywołać burzliwą dyskusję. Dla niektórych odpowiedź jest oczywista, dla innych – zaskakująca. Postaramy się rozłożyć to zagadnienie na czynniki pierwsze, zrozumieć, dlaczego to pytanie w ogóle powstaje i jakie ma konsekwencje, nie tylko w matematyce, ale i w codziennym życiu.

Zanim jednak przejdziemy do konkretów, pomyślmy, dlaczego ta kwestia jest ważna. Wyobraź sobie architekta projektującego budynek. Precyzja i dokładność w definiowaniu kształtów to podstawa. Źle zdefiniowane prostokąty i kwadraty mogą prowadzić do błędów konstrukcyjnych, a to z kolei do problemów bezpieczeństwa. Albo programista tworzący interfejs graficzny. Rozumienie relacji między różnymi kształtami pozwala mu efektywnie rozmieszczać elementy na ekranie. To tylko dwa przykłady, ale pokazują, że klarowność pojęć geometrycznych ma realny wpływ na nasze życie.

Czym w ogóle są prostokąt i kwadrat?

Zacznijmy od definicji, ponieważ to one są kluczem do zrozumienia problemu.

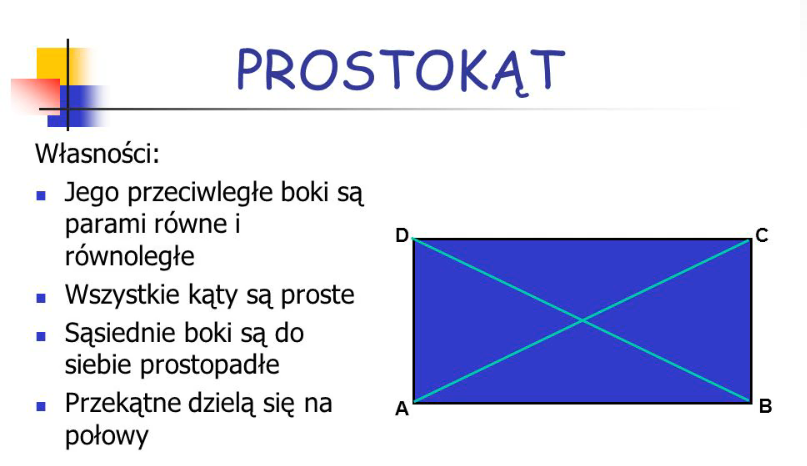
Definicja prostokąta

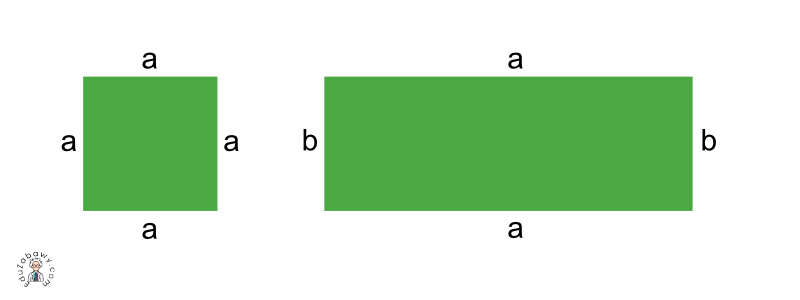
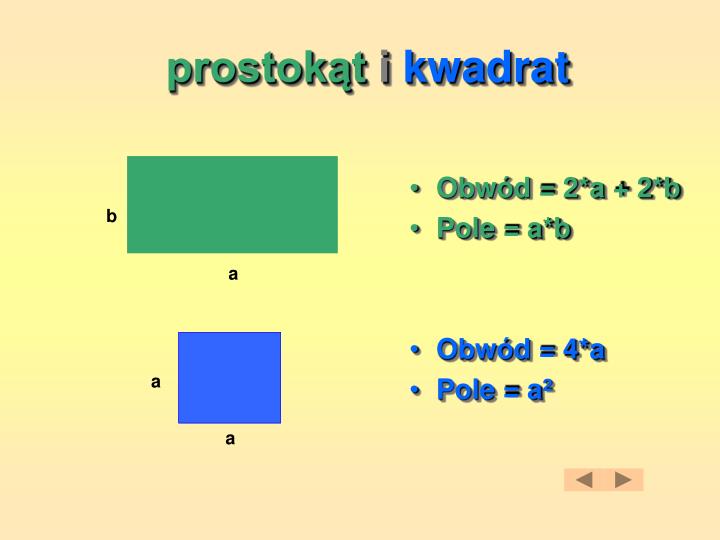
Prostokąt to czworokąt, który ma cztery kąty proste. To znaczy, że każdy z jego kątów ma miarę 90 stopni. Nie ma żadnych dodatkowych ograniczeń dotyczących długości boków. Mogą być one różne.

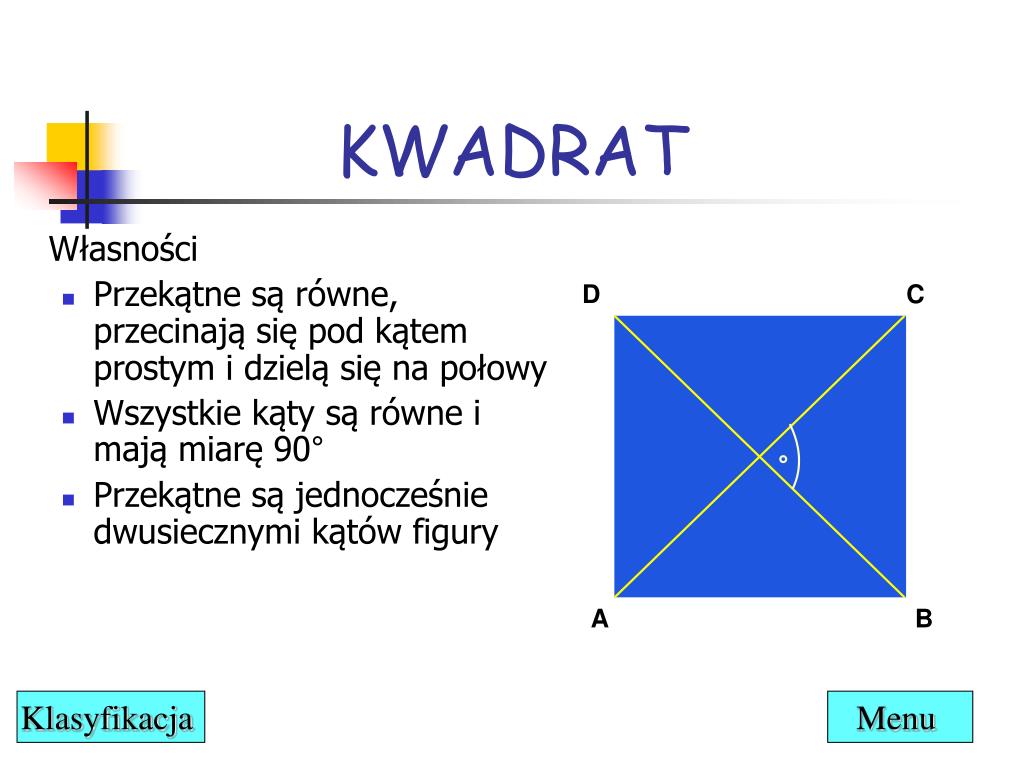
Definicja kwadratu

Kwadrat to czworokąt, który ma cztery kąty proste i wszystkie boki równej długości. To połączenie cech prostokąta (kąty proste) i rombu (równe boki).

Czy definicja kwadratu mieści się w definicji prostokąta?

Spójrzmy na to jeszcze raz. Prostokąt musi mieć tylko cztery kąty proste. Kwadrat też musi mieć cztery kąty proste, a dodatkowo wszystkie boki równe. Czyli kwadrat spełnia wszystkie warunki, które musi spełniać prostokąt, a nawet więcej.

Można to porównać do sytuacji, gdy powiemy, że "każdy owczarek niemiecki jest psem". Owczarek niemiecki ma wszystkie cechy psa (cztery nogi, szczeka, merda ogonem itd.), ale dodatkowo ma specyficzne cechy charakterystyczne dla swojej rasy. Podobnie, kwadrat ma wszystkie cechy prostokąta (cztery kąty proste), ale dodatkowo ma równe boki.

Zatem, odpowiedź brzmi: tak, każdy kwadrat jest prostokątem. Kwadrat jest szczególnym przypadkiem prostokąta.

Dlaczego więc pojawiają się wątpliwości?

Wiele osób ma problem z zaakceptowaniem tej odpowiedzi z kilku powodów:

Intuicja: W codziennym języku często używamy słów "kwadrat" i "prostokąt" zamiennie, ale jednocześnie podświadomie czujemy, że to "coś innego". Traktujemy kwadrat jako "bardzo specjalny" rodzaj prostokąta.
Wizualizacja: Często rysując prostokąt, rysujemy go tak, żeby boki miały różne długości. Kwadrat rysujemy z bokami równymi. Ta wizualna różnica utrwala w nas przekonanie, że to różne figury.
Niedokładne definicje: Nie zawsze pamiętamy dokładne definicje geometryczne. Czasami bazujemy na ogólnym wrażeniu, a nie na ścisłych regułach.

Argumenty przeciwne – i dlaczego są błędne

Czasami można usłyszeć argument, że "prostokąt ma boki o różnej długości, a kwadrat ma wszystkie boki równe, więc kwadrat nie może być prostokątem". Ten argument jest błędny, ponieważ definicja prostokąta nie wymaga, aby boki miały różną długość. Wymaga jedynie, aby miał cztery kąty proste. Równe boki to cecha, która dodatkowo charakteryzuje kwadrat, ale nie wyklucza go z kategorii prostokątów.

Inny argument może brzmieć: "Jeśli powiem, że mam prostokąt, to nie mam na myśli kwadratu". Owszem, w potocznym języku często tak jest. Jednak w matematyce, jeśli powiesz, że masz prostokąt, to nie wykluczasz, że jest to kwadrat. Po prostu nie masz pewności, czy ma on wszystkie boki równe, czy nie.

Implikacje i zastosowania

Zrozumienie relacji między kwadratem a prostokątem ma znaczenie w różnych dziedzinach:

Programowanie obiektowe: W programowaniu obiektowym można zdefiniować klasę "Prostokąt" i następnie stworzyć klasę "Kwadrat", która dziedziczy po klasie "Prostokąt". Kwadrat będzie wtedy szczególnym przypadkiem prostokąta, dziedzicząc jego właściwości i dodając własne (równe boki).
Bazy danych: Projektując bazy danych, które przechowują informacje o kształtach, ważne jest, aby prawidłowo zdefiniować relacje między nimi. Jeśli mamy tabelę "Prostokąty", to kwadraty również powinny być w niej przechowywane.
Matematyka: W dowodach matematycznych, które dotyczą prostokątów, często można stosować je również do kwadratów, ponieważ kwadraty są szczególnym przypadkiem prostokątów.

Podsumowanie i co dalej?

Podsumowując, każdy kwadrat jest prostokątem, ponieważ spełnia wszystkie warunki definicji prostokąta. Wątpliwości wynikają często z intuicji i potocznego użycia języka, a nie z matematycznych definicji. Zrozumienie tej relacji jest ważne nie tylko w matematyce, ale i w innych dziedzinach, takich jak programowanie czy architektura.

Mam nadzieję, że ten artykuł pomógł Ci lepiej zrozumieć tę kwestię. Pamiętaj, że matematyka to nie tylko wzory i obliczenia, ale przede wszystkim logiczne myślenie i precyzja w definiowaniu pojęć.

Teraz, gdy już wiesz, że kwadrat jest prostokątem, zastanów się: Czy każdy romb jest równoległobokiem? Spróbuj odpowiedzieć na to pytanie, analizując definicje obu figur. To doskonały sposób na utrwalenie wiedzy i rozwinięcie swoich umiejętności logicznego myślenia.