Czy Każdy Czworokąt Jest Trapezem

Czy kiedykolwiek zastanawiałeś się, jak sklasyfikować różne kształty? Szczególnie te, które spotykasz na co dzień – od okien po znaki drogowe? Matematyka, choć czasem wydaje się abstrakcyjna, pomaga nam porządkować świat. Jednym z podstawowych pojęć jest czworokąt, a w nim zawiera się pewna kontrowersja: czy każdy czworokąt można nazwać trapezem? To pytanie, które może wydawać się proste, ale kryje w sobie pewne niuanse.

Spróbujmy zrozumieć, skąd bierze się ta niepewność i jakie konsekwencje ma dla naszego rozumienia geometrii. To nie tylko teoretyczne rozważania. W grę wchodzi poprawne posługiwanie się terminologią, co jest kluczowe w wielu dziedzinach, od architektury po inżynierię.

Definicja trapezu – punkt wyjścia

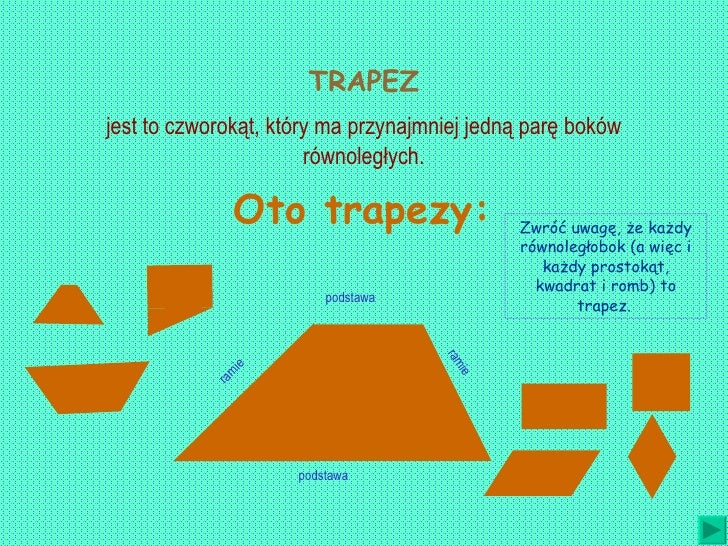
Zacznijmy od fundamentów. Co tak naprawdę definiuje trapez? Klasyczna definicja mówi, że trapez to czworokąt, który ma co najmniej jedną parę boków równoległych. Te równoległe boki nazywamy podstawami trapezu. Pozostałe dwa boki to ramiona.

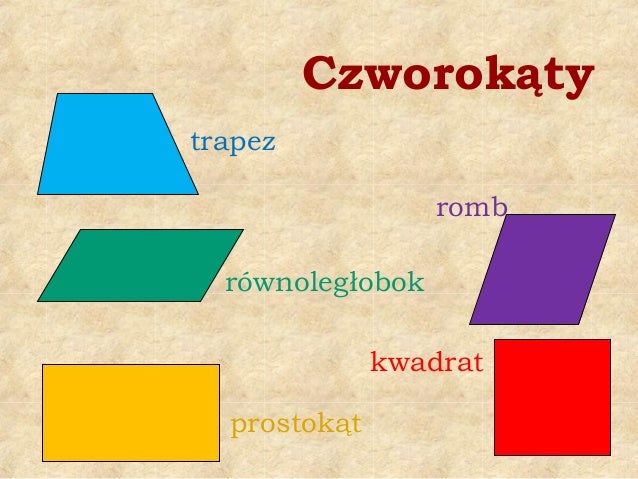
Ta definicja jest prosta i wydaje się jasna. Ale spójrzmy na inne czworokąty, takie jak prostokąty, kwadraty, romby i równoległoboki. Czy one spełniają tę definicję?

Analiza innych czworokątów

• Równoległobok: Ma dwie pary boków równoległych. Czy to oznacza, że jest trapezem? Zgodnie z definicją, tak.
• Prostokąt: Podobnie jak równoległobok, ma dwie pary boków równoległych. Zatem jest trapezem.
• Kwadrat: Jako szczególny przypadek prostokąta (i równoległoboku), również ma dwie pary boków równoległych i jest trapezem.
• Romb: Ma dwie pary boków równoległych, więc także jest trapezem.

Z powyższej analizy wynika, że wszystkie wymienione czworokąty, posiadające co najmniej jedną parę boków równoległych, spełniają definicję trapezu. Problem jednak polega na tym, że istnieją różne konwencje definicyjne, które prowadzą do zamieszania.

Dwie definicje trapezu – źródło zamieszania

W matematyce istnieją różne szkoły i tradycje, a to prowadzi do różnych definicji. W przypadku trapezu mamy dwie główne:

1. Definicja inkluzywna (szersza): Trapez to czworokąt, który ma co najmniej jedną parę boków równoległych. Zgodnie z tą definicją, równoległoboki, prostokąty, kwadraty i romby są trapezami.
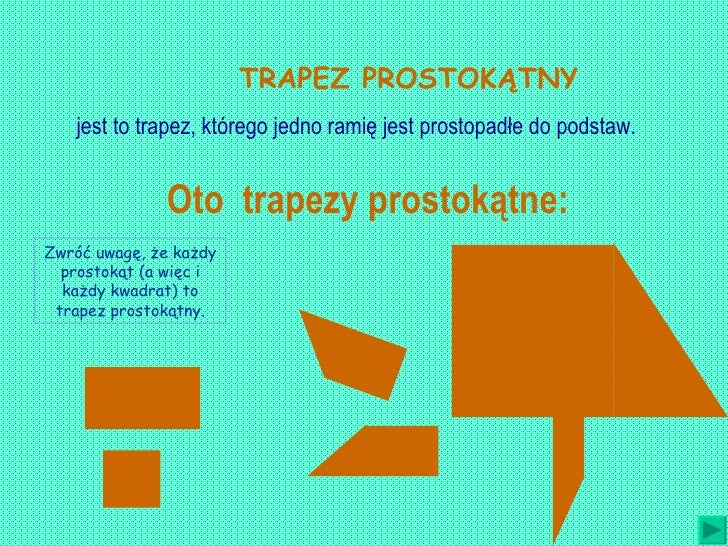
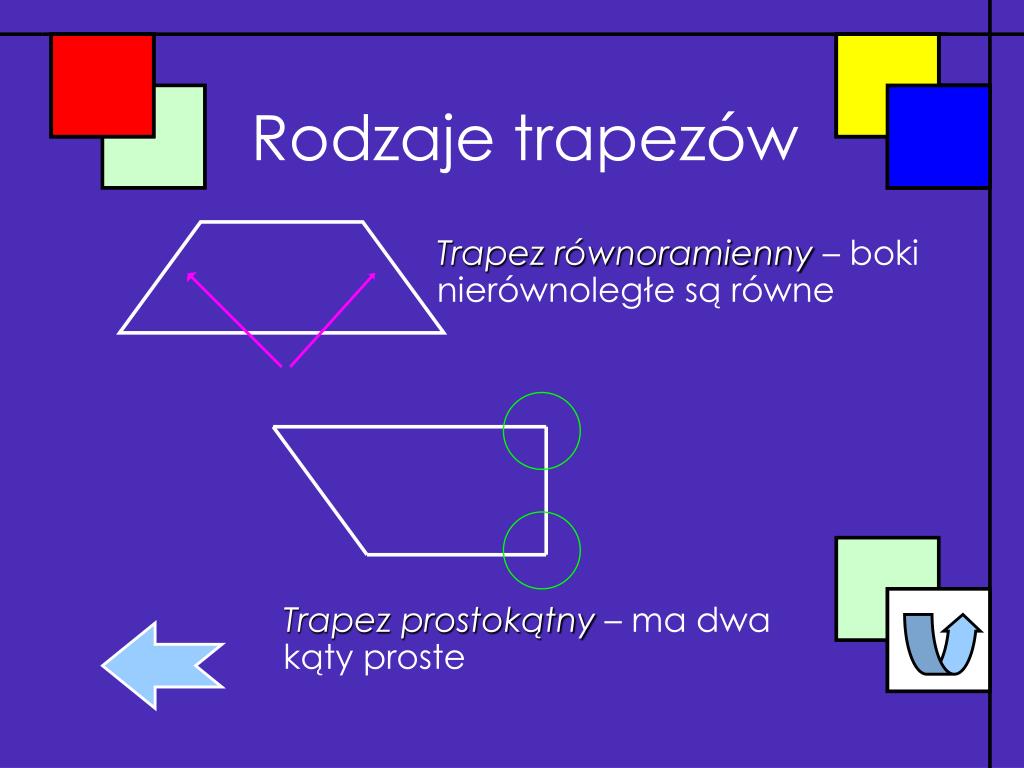
2. Definicja ekskluzywna (węższa): Trapez to czworokąt, który ma dokładnie jedną parę boków równoległych. Zgodnie z tą definicją, równoległoboki, prostokąty, kwadraty i romby nie są trapezami. Są one osobną kategorią czworokątów.

Wybór definicji ma kluczowe znaczenie dla tego, czy dany czworokąt zakwalifikujemy jako trapez. W wielu krajach, w tym w Polsce, częściej stosuje się definicję inkluzywną, co oznacza, że równoległoboki i ich szczególne przypadki są uważane za trapezy.

Argumenty za definicją inkluzywną

• Spójność teorii: Definicja inkluzywna jest bardziej spójna z ogólną tendencją w matematyce do definiowania pojęć w sposób jak najbardziej ogólny. Pozwala to na tworzenie bardziej eleganckich i uniwersalnych twierdzeń.
• Unikanie wyjątków: Używanie definicji ekskluzywnej prowadzi do tworzenia wielu wyjątków i konieczności rozważania osobnych przypadków.
• Prostsze dowody: W wielu dowodach geometrycznych łatwiej jest założyć, że równoległobok jest trapezem, niż za każdym razem rozważać go jako oddzielny przypadek.

Argumenty za definicją ekskluzywną

• Intuicyjność: Dla wielu osób definicja ekskluzywna jest bardziej intuicyjna. Uważają, że trapez powinien być "tylko" trapezem, a nie czymś bardziej specyficznym.
• Precyzja: Definicja ekskluzywna zapewnia większą precyzję w klasyfikacji czworokątów. Pozwala uniknąć sytuacji, w której dany czworokąt jest nazywany dwoma różnymi nazwami (np. jednocześnie trapezem i prostokątem).
• Jasność komunikacji: W niektórych sytuacjach definicja ekskluzywna może ułatwić komunikację, ponieważ eliminuje potencjalne nieporozumienia.

Konsekwencje wyboru definicji

Wybór definicji trapezu ma konkretne konsekwencje w praktyce. Na przykład, jeśli uczymy dzieci matematyki, powinniśmy być świadomi, którą definicję stosujemy i konsekwentnie jej używać. W podręcznikach szkolnych często brakuje jasnego określenia, którą definicję przyjęto, co może prowadzić do zamieszania.

Ponadto, w programach komputerowych do obliczeń geometrycznych również musi być jasno określone, którą definicję trapezu używa dany algorytm. W przeciwnym razie, wyniki obliczeń mogą być nieprawidłowe.

Przykładowo: Wyobraź sobie program do automatycznego rozpoznawania kształtów na obrazach. Jeśli program używa definicji inkluzywnej trapezu, rozpozna prostokąt jako trapez. Jeśli używa definicji ekskluzywnej, rozpozna prostokąt jako prostokąt, ale nie jako trapez.

Przykłady zastosowań w życiu codziennym

• Architektura: Architekci często wykorzystują trapezy w projektowaniu budynków, okien, dachów i innych elementów. W zależności od konkretnej sytuacji, mogą używać różnych definicji trapezu.
• Inżynieria: Inżynierowie wykorzystują trapezy w projektowaniu mostów, dróg, tuneli i innych konstrukcji. Podobnie jak w architekturze, wybór definicji trapezu może mieć wpływ na obliczenia i projektowanie.
• Grafika komputerowa: Graficy komputerowi wykorzystują trapezy w tworzeniu różnych kształtów i obiektów. Programy graficzne zazwyczaj oferują narzędzia do tworzenia i manipulowania trapezami, ale użytkownicy powinni być świadomi, którą definicję trapezu dany program używa.

Podsumowanie i wnioski

Odpowiedź na pytanie "Czy każdy czworokąt jest trapezem?" brzmi: to zależy. Zależy od tego, którą definicję trapezu przyjmiemy. Jeśli przyjmiemy definicję inkluzywną, to równoległoboki (a zatem i prostokąty, kwadraty oraz romby) są trapezami. Jeśli przyjmiemy definicję ekskluzywną, to nie są.

Ważne jest, aby zdawać sobie sprawę z istnienia tych dwóch definicji i wiedzieć, którą definicję stosujemy w danej sytuacji. Powinniśmy również być świadomi, że w różnych krajach i środowiskach matematycznych mogą obowiązywać różne konwencje.

Najważniejsze to:

• Zrozumieć definicję, którą się posługujesz.
• Być konsekwentnym w jej stosowaniu.
• W razie wątpliwości, dopytać o definicję używaną przez innych.

Miejmy nadzieję, że ten artykuł pomógł Ci lepiej zrozumieć problematykę definicji trapezu i jej konsekwencje. Pamiętaj, że matematyka to nie tylko suche fakty, ale również precyzja i świadomość niuansów.

Teraz zastanów się: Którą definicję trapezu uważasz za bardziej użyteczną i dlaczego?