Czy Istnieje Graniastosłup Którego Liczba Krawędzi Jest Równa 21

Czy może istnieć graniastosłup, którego liczba krawędzi wynosi dokładnie 21? To pytanie, które kryje w sobie fascynującą matematyczną zagadkę. Spróbujmy wspólnie ją rozwiązać, zagłębiając się w geometrię i własności graniastosłupów.

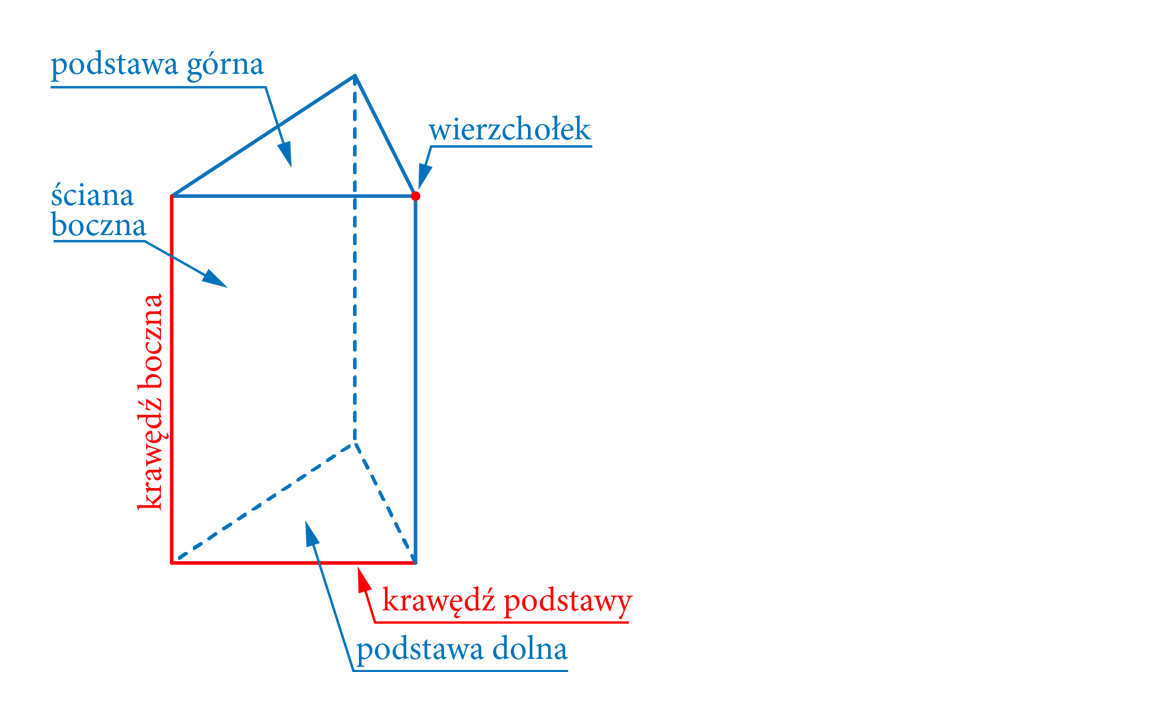
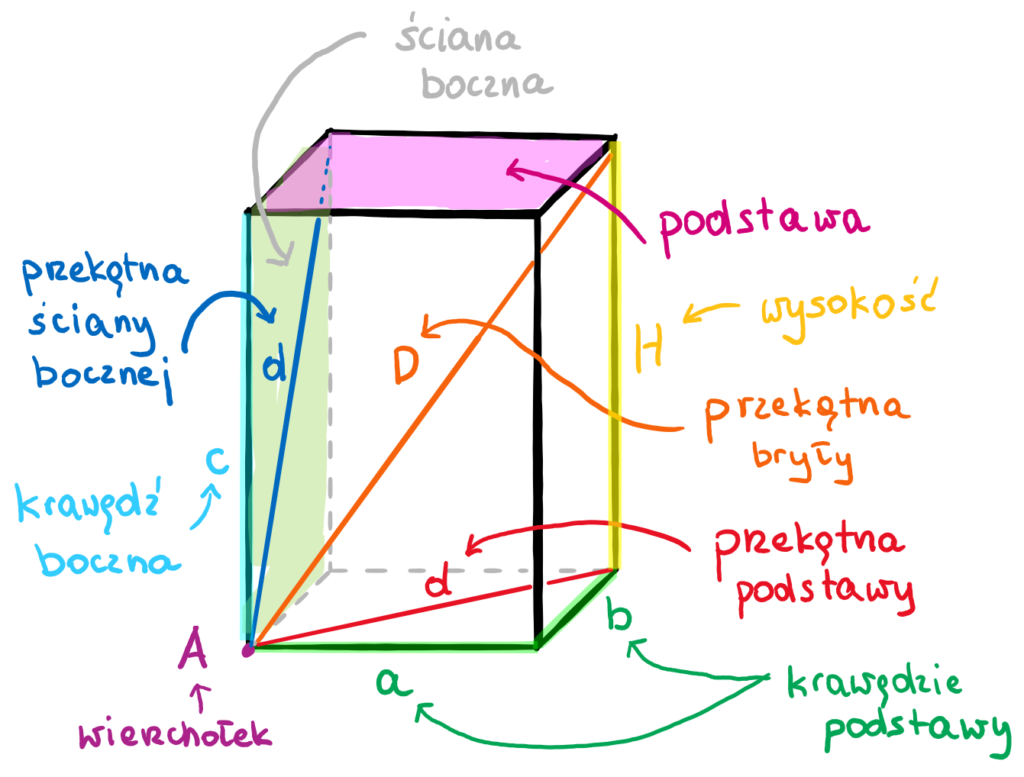
Zacznijmy od zdefiniowania, czym właściwie jest graniastosłup. Graniastosłup to wielościan, który ma dwie równoległe i przystające podstawy, będące wielokątami. Pozostałe ściany, zwane ścianami bocznymi, są równoległobokami. Najczęściej spotykane graniastosłupy to takie, których podstawy są trójkątami, czworokątami (wtedy mówimy o prostopadłościanie lub sześcianie, jeśli wszystkie ściany są kwadratami) czy pięciokątami.

Liczba wierzchołków, ścian i krawędzi w graniastosłupach podlega pewnym zależnościom. Odkrycie tych zależności pozwoli nam odpowiedzieć na tytułowe pytanie. Kluczowe będzie zrozumienie, jak liczba boków w podstawie graniastosłupa wpływa na liczbę jego krawędzi.

H2 Liczba Krawędzi w Graniastosłupie – Wzór

Aby rozwiązać nasz problem, musimy znaleźć wzór, który pozwoli nam obliczyć liczbę krawędzi w graniastosłupie na podstawie liczby boków jego podstawy. Załóżmy, że podstawa graniastosłupa jest n-kątem.

Każda z dwóch podstaw ma n krawędzi. Oprócz tego, mamy n ścian bocznych, a każda z nich ma jedną krawędź łączącą wierzchołki obu podstaw. Zatem, liczba krawędzi w graniastosłupie, którego podstawa jest n-kątem, wynosi:

K = n + n + n = 3n

Teraz możemy sprawdzić, czy istnieje takie n, dla którego K = 21.

Podstawiamy 21 do naszego wzoru:

21 = 3n

Dzielimy obie strony równania przez 3:

n = 21 / 3 = 7

Otrzymaliśmy n = 7. Co to oznacza? Oznacza to, że istnieje graniastosłup, którego liczba krawędzi wynosi 21. Jest to graniastosłup, którego podstawą jest siedmiokąt. Taki graniastosłup posiada dwie podstawy w kształcie siedmiokąta oraz siedem ścian bocznych w kształcie równoległoboków.

Możemy to jeszcze raz sprawdzić. Siedmiokąt ma 7 krawędzi. Mamy dwie takie podstawy, czyli 2 * 7 = 14 krawędzi. Dodatkowo mamy 7 krawędzi łączących obie podstawy. Razem 14 + 7 = 21 krawędzi. Zgadza się!

Spójrzmy na to z innej perspektywy. Liczba wierzchołków w graniastosłupie, którego podstawą jest n-kąt, wynosi 2n. W naszym przypadku, gdy n = 7, mamy 2 * 7 = 14 wierzchołków. Liczba ścian wynosi n + 2, czyli w naszym przypadku 7 + 2 = 9 ścian. Możemy sprawdzić, czy spełnione jest twierdzenie Eulera dla wielościanów, które mówi, że:

W - K + S = 2, gdzie W to liczba wierzchołków, K to liczba krawędzi, a S to liczba ścian.

W naszym przypadku:

14 - 21 + 9 = 2

2 = 2

Twierdzenie Eulera jest spełnione, co dodatkowo potwierdza, że nasze obliczenia są prawidłowe.

Rozważmy teraz inne liczby krawędzi. Czy istnieje graniastosłup, który ma 20 krawędzi? Zgodnie z naszym wzorem, K = 3n, więc 20 = 3n. Dzieląc obie strony przez 3, otrzymujemy n = 20 / 3 = 6.666... . Liczba boków podstawy musi być liczbą naturalną, a 6.666... nie jest liczbą naturalną. Zatem nie istnieje graniastosłup, który ma 20 krawędzi.

A co z graniastosłupem, który ma 24 krawędzie? 24 = 3n, więc n = 24 / 3 = 8. Zatem istnieje graniastosłup, którego podstawa jest ośmiokątem i ma on 24 krawędzie.

H2 Własności Graniastosłupów

Graniastosłupy charakteryzują się szeregiem interesujących własności. Jak już wspomnieliśmy, podstawy graniastosłupa są zawsze przystające i równoległe. Ściany boczne są równoległobokami, a w przypadku graniastosłupów prostych (czyli takich, w których ściany boczne są prostopadłe do podstaw) są prostokątami.

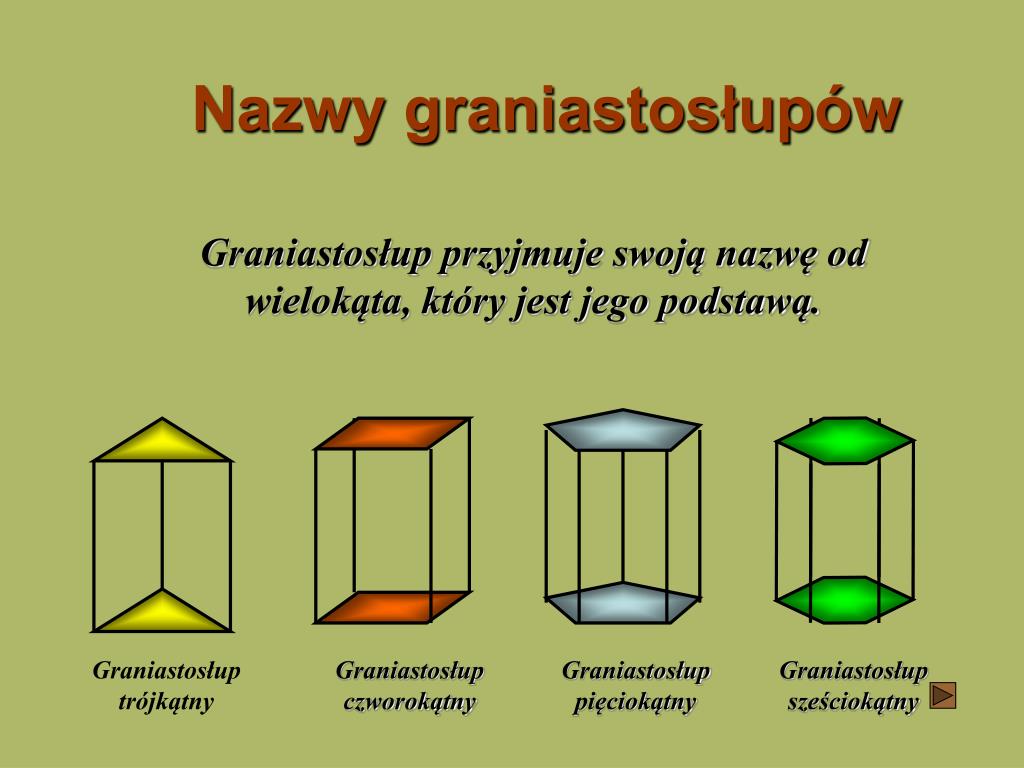
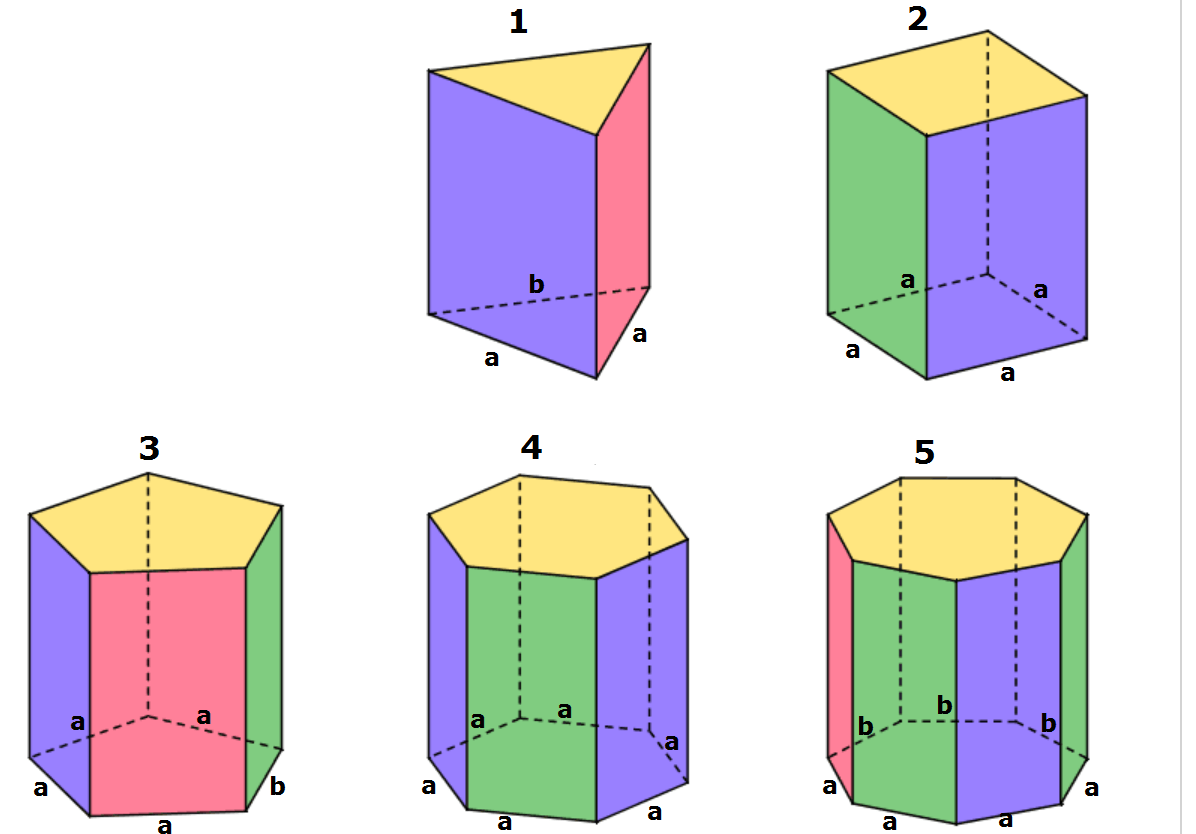
W zależności od kształtu podstawy, graniastosłupy dzielimy na trójkątne, czworokątne, pięciokątne itd. Graniastosłup czworokątny, którego wszystkie ściany są prostokątami, nazywamy prostopadłościanem. Szczególnym przypadkiem prostopadłościanu jest sześcian, w którym wszystkie ściany są kwadratami.

Objętość graniastosłupa obliczamy, mnożąc pole podstawy przez wysokość graniastosłupa (czyli odległość między podstawami). Pole powierzchni całkowitej graniastosłupa to suma pól wszystkich jego ścian.

H2 Zastosowania Graniastosłupów

Graniastosłupy, ze względu na swoje proste i regularne kształty, znajdują szerokie zastosowanie w różnych dziedzinach życia. Architektura pełna jest przykładów budynków o kształcie graniastosłupów, takich jak wieżowce czy bloki mieszkalne. W inżynierii, graniastosłupy wykorzystywane są jako elementy konstrukcyjne, np. belki czy słupy. W przemyśle, opakowania w kształcie graniastosłupów są bardzo popularne ze względu na łatwość przechowywania i transportu.

W optyce, pryzmaty (które są rodzajem graniastosłupa) służą do rozszczepiania światła białego na widmo kolorów. W matematyce i geometrii, graniastosłupy stanowią ważny obiekt badań, pozwalając na analizę i zrozumienie własności wielościanów.

H2 Podsumowanie

Odpowiedź na pytanie, czy istnieje graniastosłup o 21 krawędziach, jest twierdząca. Jest to graniastosłup, którego podstawą jest siedmiokąt. Znaleźliśmy wzór na obliczanie liczby krawędzi w graniastosłupie, K = 3n, gdzie n to liczba boków podstawy. Dzięki temu wzorowi możemy łatwo sprawdzić, czy istnieje graniastosłup o danej liczbie krawędzi. Zrozumieliśmy również, że liczba boków podstawy musi być liczbą naturalną, aby graniastosłup mógł istnieć. Przeanalizowaliśmy także własności graniastosłupów i ich zastosowania w różnych dziedzinach. Mam nadzieję, że ta matematyczna podróż była dla Ciebie pouczająca i interesująca!