Czy Dwie Półproste O Wspólnym Początku Zawsze Tworzą Prostą

Często uczniowie zastanawiają się, czy dwie półproste, które mają wspólny punkt początkowy, automatycznie tworzą linię prostą. Odpowiedź na to pytanie jest bardzo ważna, aby zrozumieć podstawy geometrii. Przejdźmy zatem do szczegółów, żeby wszystko stało się jasne.

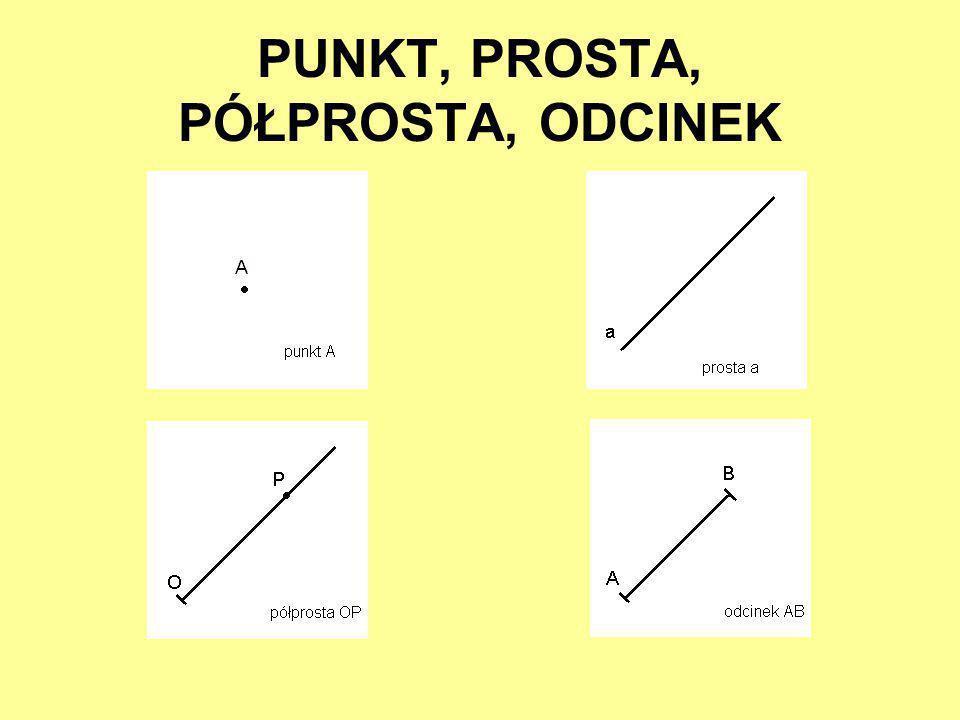
Półprosta to część prostej, która ma swój początek w pewnym punkcie, ale rozciąga się w nieskończoność w jednym kierunku. Wyobraź sobie promień słońca - zaczyna się w słońcu i biegnie bez końca w jednym kierunku. Punkt, z którego "wyrasta" półprosta, nazywamy jej początkiem.

Teraz wyobraźmy sobie, że mamy dwie takie półproste, które "wychodzą" z tego samego punktu. Czy zawsze utworzą one prostą? Odpowiedź brzmi: nie, nie zawsze.

Żeby dwie półproste o wspólnym początku utworzyły prostą, muszą spełniać pewien warunek. Spróbujmy to sobie wizualizować.

Kiedy Dwie Półproste Tworzą Prostą?

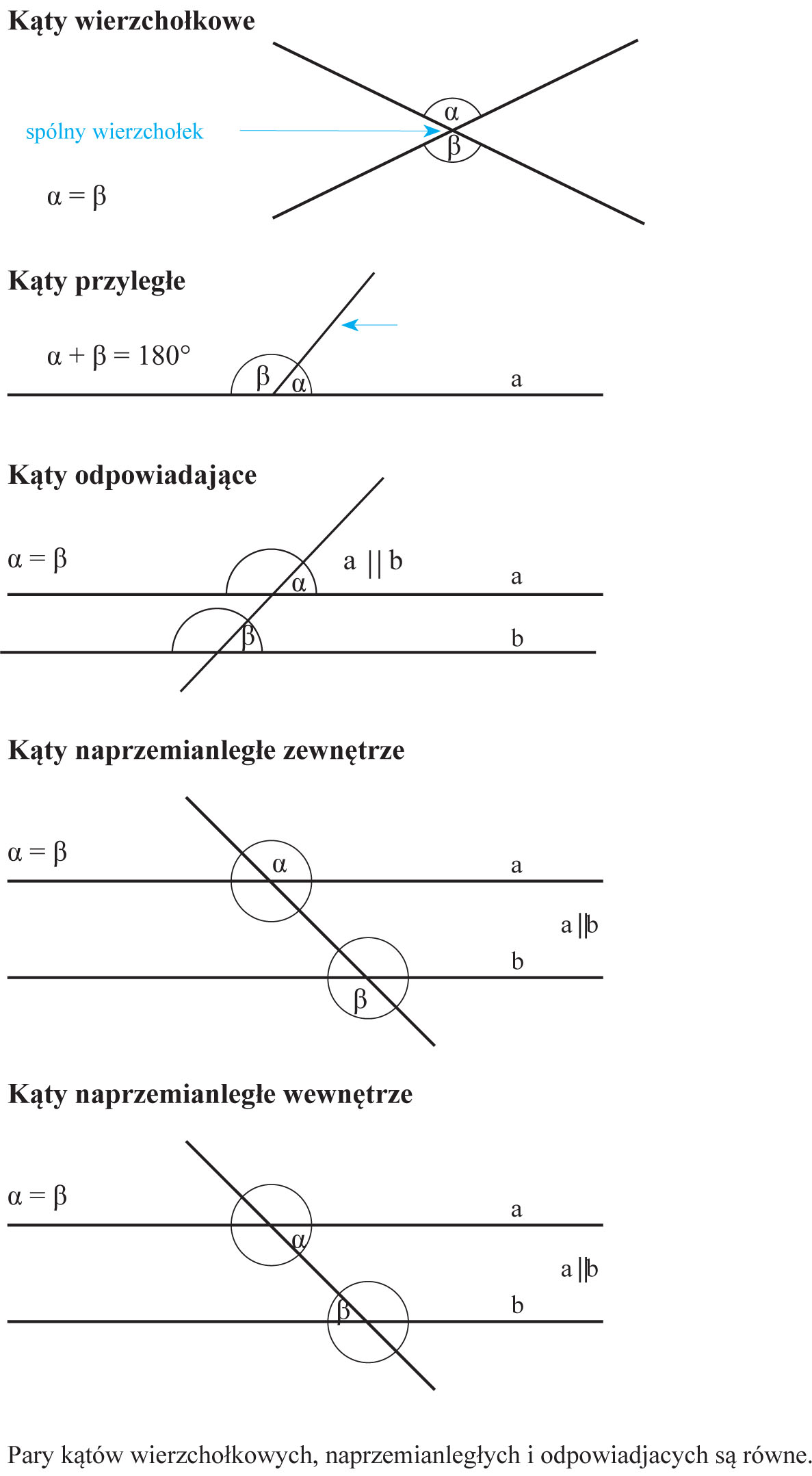
Wyobraź sobie, że masz linijkę i na kartce rysujesz punkt. To będzie nasz wspólny początek obu półprostych. Teraz od tego punktu rysujesz linię w jednym kierunku. To jest pierwsza półprosta. Żeby druga półprosta utworzyła razem z nią prostą, musi być narysowana w dokładnie przeciwnym kierunku. Czyli, jeżeli przedłuży ona pierwszą półprostą w przeciwnym kierunku, to razem utworzą jedną, długą, prostą linię.

Mówiąc bardziej formalnie, półproste muszą być przeciwne. Co to oznacza? Oznacza to, że kąt między nimi musi wynosić 180 stopni. Pomyśl o tym jak o rozłożonej książce. Grzbiet książki to nasz punkt początkowy, a dwie otwarte strony to półproste. Jeżeli strony leżą płasko na stole (tworząc kąt 180 stopni), to tworzą razem linię prostą.

Jeśli jednak narysujesz drugą półprostą w innym kierunku (np. pod kątem prostym, czyli 90 stopni, do pierwszej), to nie uzyskasz prostej. Otrzymasz po prostu kąt, czyli obszar między dwiema półprostymi.

Żeby to jeszcze lepiej zobrazować, pomyśl o zegarze. O godzinie 6:00 wskazówka godzinowa i minutowa tworzą prostą linię. Są to półproste o wspólnym początku (środek zegara), które są skierowane w przeciwnych kierunkach. Ale o godzinie 3:00 już tak nie jest. Wskazówki nadal mają wspólny początek, ale nie tworzą prostej.

Przykłady i Kontrprzykłady

• Przykład 1 (Prosta): Dwie osoby stoją plecami do siebie. Wyobraź sobie, że każda z nich wyciąga rękę prosto przed siebie. Ich ręce (półproste) mają wspólny punkt (miejsce, gdzie stykają się ich plecy) i tworzą prostą linię.
• Przykład 2 (Prosta): Tor kolejowy. Dwa tory rozchodzące się w przeciwnych kierunkach od jednego punktu na stacji.
• Przykład 3 (Nie Prosta): Rozwidlenie drogi w kształcie litery "V". Dwie drogi (półproste) rozchodzą się od jednego punktu (rozwidlenie), ale nie tworzą prostej.
• Przykład 4 (Nie Prosta): Wskazówki zegara o godzinie 15:00. Mają wspólny początek, ale nie leżą na jednej linii prostej.

Podsumowując, dwie półproste o wspólnym początku tworzą prostą tylko wtedy, gdy są przeciwne, czyli gdy leżą na jednej prostej i są skierowane w przeciwnych kierunkach. Inaczej mówiąc, kąt między nimi musi wynosić 180 stopni.

Warto pamiętać o tej definicji, ponieważ często pojawia się ona w zadaniach z geometrii. Zrozumienie, kiedy półproste tworzą prostą, a kiedy nie, jest kluczowe do rozwiązywania problemów i budowania solidnych podstaw wiedzy matematycznej. Jeśli nadal masz wątpliwości, spróbuj narysować kilka przykładów półprostych i sprawdź, czy tworzą one prostą. Eksperymentowanie z rysunkami pomoże Ci lepiej zrozumieć tę koncepcję. Im więcej przykładów zobaczysz i sam narysujesz, tym łatwiej będzie Ci to zapamiętać i stosować w praktyce.

Pamiętaj, że w matematyce bardzo ważne jest zrozumienie definicji i pojęć. Samo zapamiętywanie wzorów nie wystarczy. Trzeba wiedzieć, skąd się one biorą i co oznaczają. W przypadku półprostych i prostych, wizualizacja i przykłady są bardzo pomocne. Spróbuj szukać przykładów w swoim otoczeniu. Zobaczysz, że geometria jest wszędzie!

A teraz spróbuj odpowiedzieć na pytanie: czy dwie półproste, które pokrywają się, tworzą prostą? Zastanów się nad tym i pamiętaj o tym, co omówiliśmy wcześniej. Powodzenia!