Czy Dane Punkty Są Symetryczne Względem Narysowanej Prostej

Hej klaso! Widzę, że macie pytania dotyczące symetrii punktów względem prostej. Spokojnie, rozjaśnijmy to! Sprawdzanie, czy dwa punkty są symetryczne względem narysowanej prostej, wydaje się skomplikowane, ale tak naprawdę to proces składający się z kilku prostych kroków. Chcę Wam to wytłumaczyć w taki sposób, żebyście mogli sami rozwiązywać te zadania bez problemu.

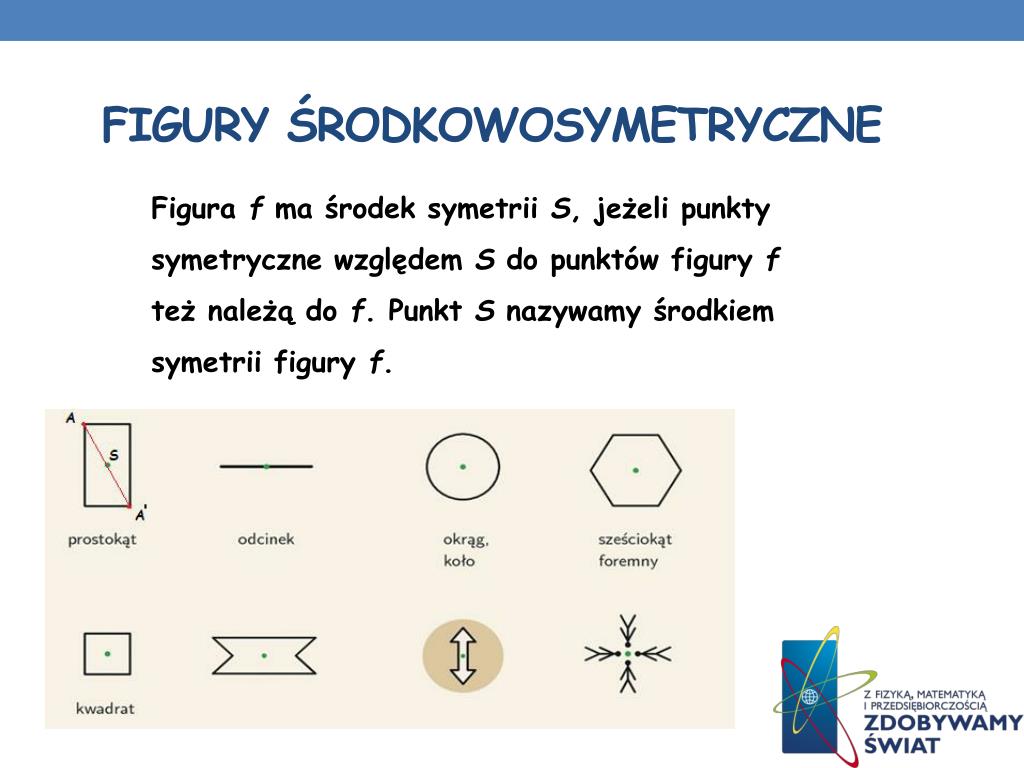
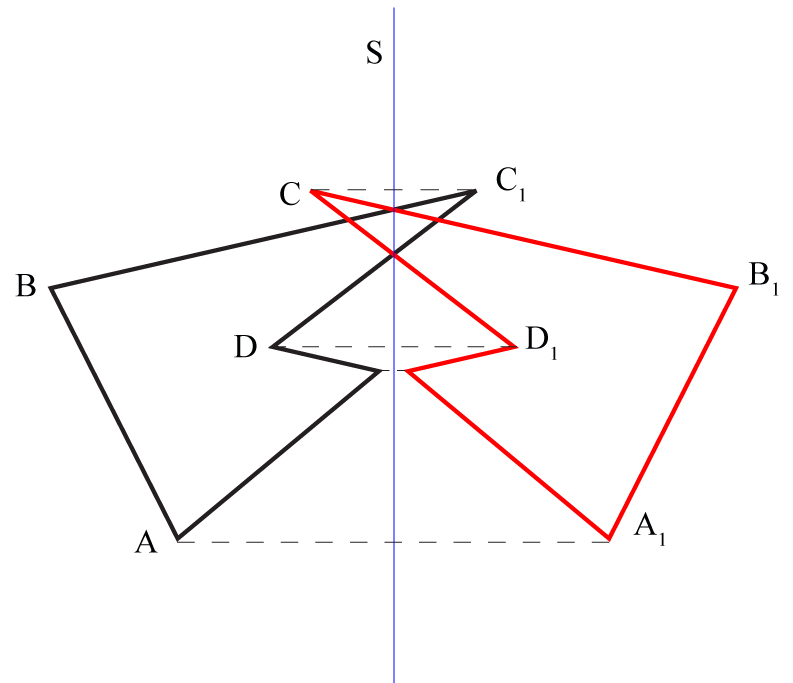
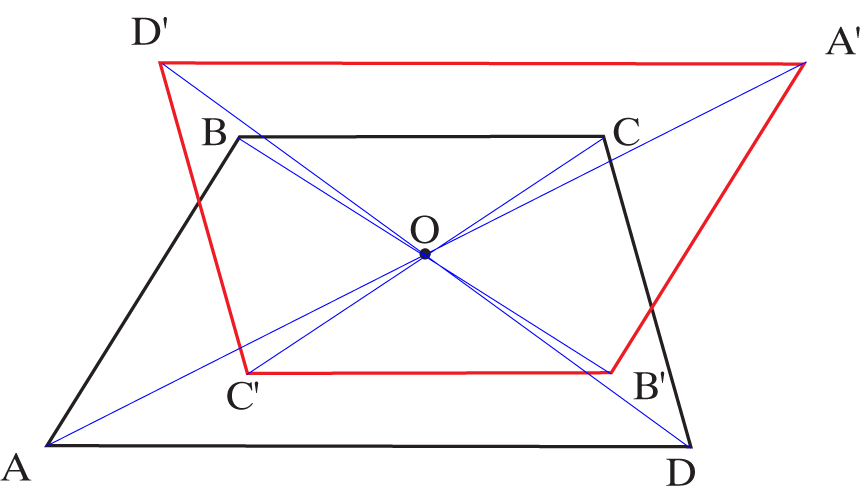
Na początek musimy zrozumieć, co to w ogóle znaczy, że punkty są symetryczne względem prostej. Wyobraźcie sobie, że prosta, względem której sprawdzamy symetrię, to takie lustro. Punkty symetryczne to te, które odbijają się w tym lustrze idealnie. Oznacza to, że odległość każdego z tych punktów od prostej (lustra) jest taka sama, a linia łącząca te punkty jest prostopadła do prostej. Brzmi trochę zawile? Spokojnie, przejdźmy do konkretów.

Pierwszym krokiem jest sprawdzenie, czy linia łącząca dwa punkty jest prostopadła do naszej prostej. Jak to zrobić? Najprościej, jeśli mamy narysowaną prostą i punkty w układzie współrzędnych. Wtedy możemy "na oko" ocenić, czy kąt między nimi jest prosty. Jeśli jednak zależy nam na precyzyjnym sprawdzeniu, musimy posłużyć się matematyką.

Wyobraźcie sobie, że punkty, które sprawdzamy to A i B, a prosta nazywa się "k". Potrzebujemy znaleźć równanie prostej przechodzącej przez punkty A i B. Jeśli mamy współrzędne punktów A i B (np. A(x1, y1) i B(x2, y2)), możemy obliczyć współczynnik kierunkowy tej prostej, oznaczmy go jako "mAB". Wzór na to jest następujący:

mAB = (y2 - y1) / (x2 - x1)

Teraz, jeśli znamy współczynnik kierunkowy prostej "k" (oznaczmy go jako "mk"), to żeby sprawdzić, czy proste są prostopadłe, musimy zweryfikować, czy iloczyn ich współczynników kierunkowych jest równy -1. Czyli:

mAB * mk = -1

Jeśli ten warunek jest spełniony, to znaczy, że prosta AB jest prostopadła do prostej "k". Super! Mamy pierwszy krok za sobą. Jeśli nie jest spełniony, to od razu wiemy, że punkty A i B nie są symetryczne względem prostej "k" i nie musimy dalej liczyć.

Odległość Punktów od Prostej

Załóżmy, że sprawdziliśmy już prostopadłość i wszystko się zgadza. Teraz musimy upewnić się, że odległości punktów A i B od prostej "k" są takie same. Tutaj zaczyna się zabawa z obliczeniami, ale nie bójcie się, krok po kroku dojdziemy do celu.

Potrzebujemy wzoru na odległość punktu od prostej. Jeśli mamy punkt P(x0, y0) i prostą opisaną równaniem ogólnym Ax + By + C = 0, to odległość punktu P od prostej możemy obliczyć ze wzoru:

d = |Ax0 + By0 + C| / √(A² + B²)

Wygląda to trochę strasznie, ale zobaczcie, że potrzebujemy tylko podstawić współrzędne punktu i współczynniki z równania prostej.

Teraz, żeby sprawdzić, czy punkty A i B są symetryczne względem prostej "k", musimy obliczyć odległość punktu A od prostej "k" (oznaczmy ją jako dA) i odległość punktu B od prostej "k" (oznaczmy ją jako dB).

Jeśli dA = dB, to znaczy, że punkty A i B znajdują się w tej samej odległości od prostej "k". W połączeniu z faktem, że prosta AB jest prostopadła do prostej "k", oznacza to, że punkty A i B są symetryczne względem prostej "k".

Podsumowując:

1. Sprawdzamy, czy prosta przechodząca przez punkty A i B jest prostopadła do prostej "k".
2. Obliczamy odległość punktu A od prostej "k".
3. Obliczamy odległość punktu B od prostej "k".
4. Porównujemy odległości dA i dB. Jeśli są równe, to punkty A i B są symetryczne względem prostej "k".

Przykład:

Załóżmy, że mamy punkty A(1, 2) i B(5, 2) oraz prostą "k" o równaniu x = 3.

1. Prostopadłość: Prosta przechodząca przez punkty A i B jest pozioma (y = 2). Prosta x = 3 jest pionowa. Proste poziome i pionowe są prostopadłe, więc warunek prostopadłości jest spełniony. Możemy też to sprawdzić obliczając współczynnik kierunkowy prostej AB. mAB = (2-2) / (5-1) = 0. Współczynnik kierunkowy prostej pionowej nie istnieje, ale wiemy, że każda prosta pozioma (o współczynniku kierunkowym równym 0) jest prostopadła do prostej pionowej.

2. Odległość punktu A od prostej k: Równanie prostej k to x - 3 = 0. Zatem A=1, B=0, C=-3. x0=1, y0=2. dA = |11 + 02 - 3| / √(1² + 0²) = |-2| / √1 = 2

3. Odległość punktu B od prostej k: Równanie prostej k to x - 3 = 0. Zatem A=1, B=0, C=-3. x0=5, y0=2. dB = |15 + 02 - 3| / √(1² + 0²) = |2| / √1 = 2

4. Porównanie odległości: dA = dB = 2.

Zatem punkty A(1, 2) i B(5, 2) są symetryczne względem prostej x = 3. Możecie to sobie narysować i zobaczyć, że to prawda!

Pamiętajcie, że najważniejsze jest zrozumienie koncepcji symetrii i to, co ona oznacza geometrycznie. Wzory są tylko narzędziami, które pomagają nam to sprawdzić matematycznie. Im więcej ćwiczycie, tym łatwiej będzie Wam rozwiązywać takie zadania. Spróbujcie rozwiązać kilka przykładów, zmieniając współrzędne punktów i równania prostych. Zobaczycie, że to naprawdę nie jest takie trudne, jak się wydaje na początku! Powodzenia!

I jeszcze jedna ważna rzecz: jeśli prosta, względem której sprawdzamy symetrię, jest pozioma (np. y = 4) lub pionowa (np. x = 2), to obliczenia są znacznie prostsze! Wtedy odległość punktu od prostej pionowej to po prostu różnica między współrzędną x punktu i wartością x prostej (wartość bezwzględna z tej różnicy). Podobnie, odległość punktu od prostej poziomej to różnica między współrzędną y punktu i wartością y prostej (wartość bezwzględna z tej różnicy). Warto o tym pamiętać, bo często takie proste są w zadaniach!

Mam nadzieję, że to wyjaśnienie Wam pomogło. Jeśli macie jeszcze jakieś pytania, śmiało pytajcie! Jestem tutaj, żeby Wam pomóc zrozumieć matematykę!