Co To Są Proste Prostopadłe

Czy kiedykolwiek zastanawiałeś się, jak architekci budują proste i stabilne budynki? Albo jak nawigacja GPS potrafi precyzyjnie wyznaczyć Twoją trasę? Odpowiedź często tkwi w prostych, ale fundamentalnych zasadach geometrii, a konkretnie w zrozumieniu, czym są proste prostopadłe. Ten artykuł jest dla Ciebie, niezależnie od tego, czy jesteś uczniem mierzącym się z zadaniami z matematyki, studentem inżynierii, czy po prostu osobą ciekawą świata. Razem odkryjemy definicję, właściwości i praktyczne zastosowania prostych prostopadłych.

Co to są proste prostopadłe? Definicja i podstawy

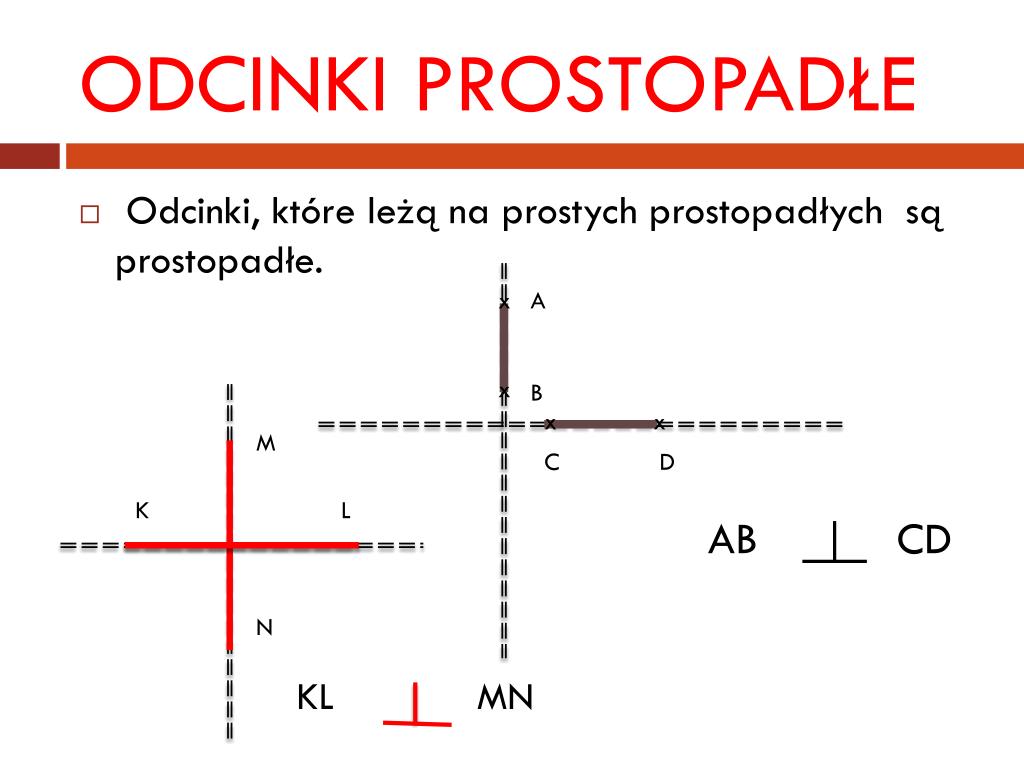
Zacznijmy od definicji. Proste prostopadłe to dwie proste, które przecinają się pod kątem prostym, czyli 90 stopni. Wyobraź sobie literę "T" – jej pozioma i pionowa kreska tworzą dokładnie taki kąt. Ale co to właściwie oznacza w języku matematyki?

Aby lepiej to zrozumieć, przypomnijmy sobie podstawowe pojęcia:

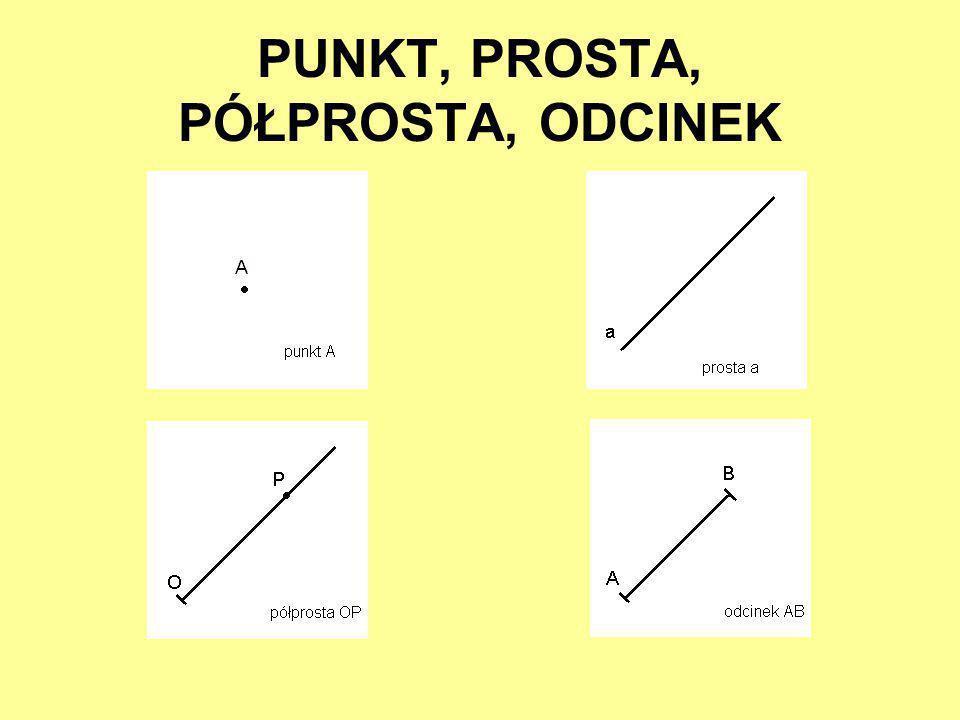
Prosta: Nieskończenie długa linia, która nie ma początku ani końca.
Punkt: Konkretna lokalizacja w przestrzeni.
Odcinek: Część prostej ograniczona dwoma punktami, zwanymi końcami.
Kąt: Figura geometryczna utworzona przez dwie półproste wychodzące z jednego punktu (wierzchołka).

Kiedy dwie proste przecinają się, tworzą cztery kąty. Jeśli jeden z tych kątów jest prosty (90 stopni), to wszystkie cztery kąty są proste, a te proste nazywamy prostopadłymi.

Oznaczenia i symbole

W matematyce używamy specjalnych symboli, aby zaznaczyć, że proste są prostopadłe. Najczęściej używany symbol to odwrócona litera "T" (⊥). Zatem, jeśli prosta 'a' jest prostopadła do prostej 'b', zapisujemy to jako a ⊥ b.

Jak rozpoznać proste prostopadłe?

Istnieje kilka sposobów, aby sprawdzić, czy dwie proste są prostopadłe:

Pomiar kąta: Najprostszy sposób to użycie kątomierza. Jeśli kąt między prostymi wynosi 90 stopni, to są one prostopadłe.
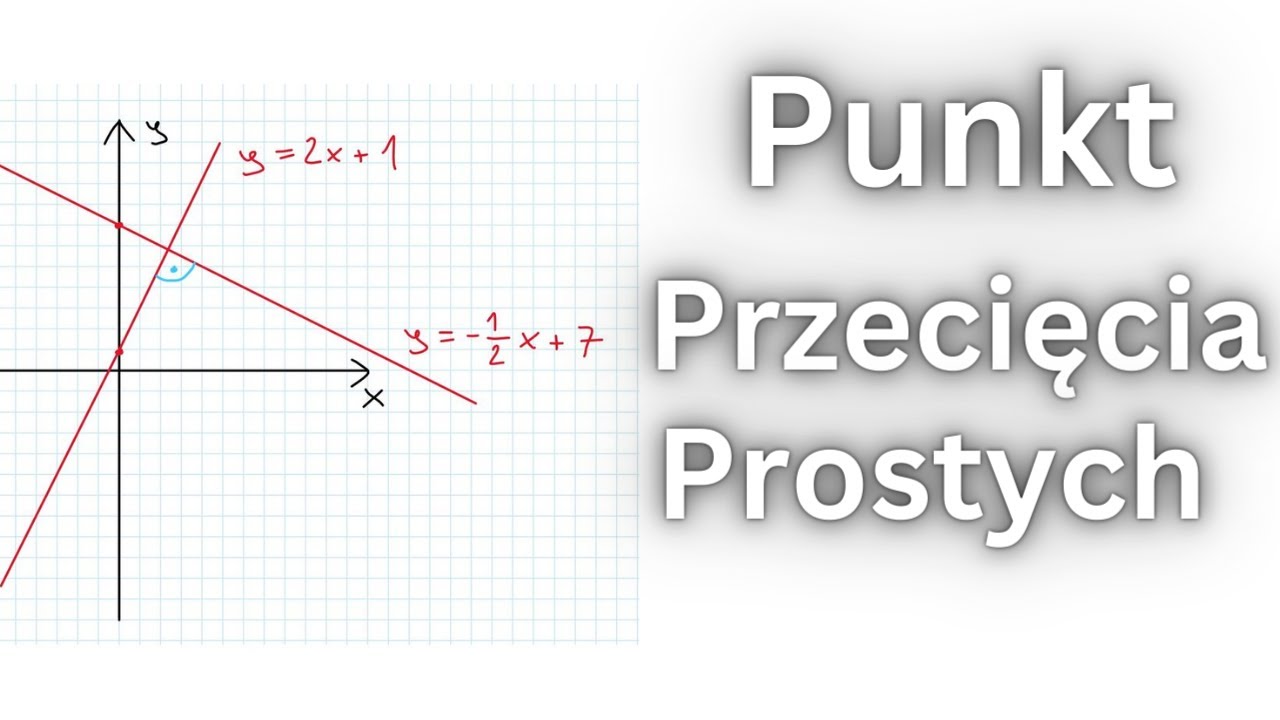
Sprawdzenie równań: Jeśli mamy równania prostych w postaci kierunkowej (y = ax + b), możemy obliczyć ich współczynniki kierunkowe (a). Dwie proste są prostopadłe, jeśli iloczyn ich współczynników kierunkowych wynosi -1. Czyli, jeśli równania prostych to y = a₁x + b₁ i y = a₂x + b₂, to a₁ * a₂ = -1, aby proste były prostopadłe.
Użycie twierdzenia Pitagorasa: Możemy wybrać trzy punkty: punkt przecięcia prostych oraz po jednym punkcie na każdej prostej. Utworzy się trójkąt. Jeśli ten trójkąt jest prostokątny, a punkt przecięcia prostych jest wierzchołkiem kąta prostego, to proste są prostopadłe. Możemy to sprawdzić za pomocą twierdzenia Pitagorasa (a² + b² = c²).

Przykład: Rozważmy proste o równaniach y = 2x + 1 i y = -0.5x + 3. Współczynnik kierunkowy pierwszej prostej wynosi 2, a drugiej -0.5. Iloczyn tych współczynników to 2 * (-0.5) = -1. Zatem, te proste są prostopadłe.

Praktyczne zastosowania prostych prostopadłych

Proste prostopadłe znajdują szerokie zastosowanie w wielu dziedzinach życia, od architektury po informatykę.

Architektura i budownictwo

W budownictwie proste prostopadłe są niezbędne do tworzenia stabilnych i równych konstrukcji. Budynki muszą mieć ściany prostopadłe do podłogi, aby były bezpieczne i funkcjonalne. Inżynierowie używają poziomnic i kątomierzy, aby zapewnić, że elementy konstrukcyjne są ustawione pod kątem prostym.

Geodezja i kartografia

W geodezji proste prostopadłe są wykorzystywane do tworzenia map i planów. Systemy współrzędnych, takie jak układ współrzędnych geograficznych (szerokość i długość geograficzna) opierają się na idei prostopadłych linii, które przecinają się pod kątem prostym, tworząc siatkę odniesienia.

Informatyka i grafika komputerowa

W grafice komputerowej proste prostopadłe są wykorzystywane do tworzenia obrazów 2D i 3D. Algorytmy renderowania często wykorzystują informacje o kątach prostych, aby realistycznie odwzorować światło i cień. Ponadto, w programowaniu gier, proste prostopadłe są używane do detekcji kolizji obiektów i obliczania trajektorii ruchu.

Nawigacja

Systemy nawigacji GPS wykorzystują triangulację, która opiera się na geometrycznych relacjach, w tym na prostopadłości. Satelity GPS wysyłają sygnały do odbiornika, a odbiornik oblicza swoją pozycję na podstawie odległości od kilku satelitów. Te obliczenia często wykorzystują kąty proste i prostopadłe linie, aby uzyskać dokładne wyniki.

Życie codzienne

Nawet w życiu codziennym spotykamy się z prostymi prostopadłymi. Kiedy wieszamy obraz na ścianie, intuicyjnie staramy się, aby był prostopadły do podłogi. Kiedy ustawiamy meble w pokoju, często dbamy o to, aby tworzyły kąty proste z ścianami. Te proste, codzienne czynności pokazują, jak głęboko geometria przenika nasze życie.

Właściwości prostych prostopadłych

Proste prostopadłe mają kilka istotnych właściwości:

Tworzą kąty proste: To podstawowa cecha.
Minimalna odległość: Odległość od punktu do prostej jest najkrótsza, gdy linia łącząca ten punkt z prostą jest do niej prostopadła.
Konstrukcja: Proste prostopadłe można łatwo konstruować za pomocą cyrkla i linijki.
Relacje z innymi figurami geometrycznymi: Proste prostopadłe odgrywają kluczową rolę w definicjach i właściwościach kwadratów, prostokątów, trójkątów prostokątnych i innych figur.

Podsumowanie i dalsza eksploracja

Mam nadzieję, że ten artykuł pomógł Ci zrozumieć, czym są proste prostopadłe i jakie mają znaczenie. To fundamentalne pojęcie geometrii, które odgrywa kluczową rolę w wielu dziedzinach życia. Teraz, gdy masz solidne podstawy, możesz zgłębiać dalsze zagadnienia związane z geometrią, takie jak:

Geometria euklidesowa: Podstawy geometrii, w tym aksjomaty i twierdzenia dotyczące punktów, prostych, płaszczyzn i figur geometrycznych.
Trygonometria: Nauka o związkach między kątami i bokami trójkątów, w tym funkcji trygonometrycznych (sinus, cosinus, tangens).
Geometria analityczna: Połączenie geometrii z algebrą, które pozwala na opisywanie figur geometrycznych za pomocą równań i współrzędnych.

Pamiętaj, że matematyka to nie tylko zbiór wzorów i reguł, ale przede wszystkim narzędzie do rozwiązywania problemów i zrozumienia świata. Kontynuuj naukę i odkrywaj piękno i potęgę geometrii! Spróbuj poszukać w swoim otoczeniu przykładów prostych prostopadłych – zobaczysz, że są wszędzie. Powodzenia!