Co To Mianownik W Ułamku

Ułamki są fundamentalnym elementem matematyki, używanym do reprezentowania części całości. Choć na pierwszy rzut oka mogą wydawać się proste, kryją w sobie szereg niuansów i zasad, których zrozumienie jest kluczowe do dalszej nauki matematyki. Jednym z najważniejszych elementów ułamka jest jego mianownik. W tym artykule przyjrzymy się bliżej temu, czym jest mianownik, jaką pełni rolę w ułamku, oraz jakie konsekwencje wynikają z jego wartości.

Czym jest Mianownik?

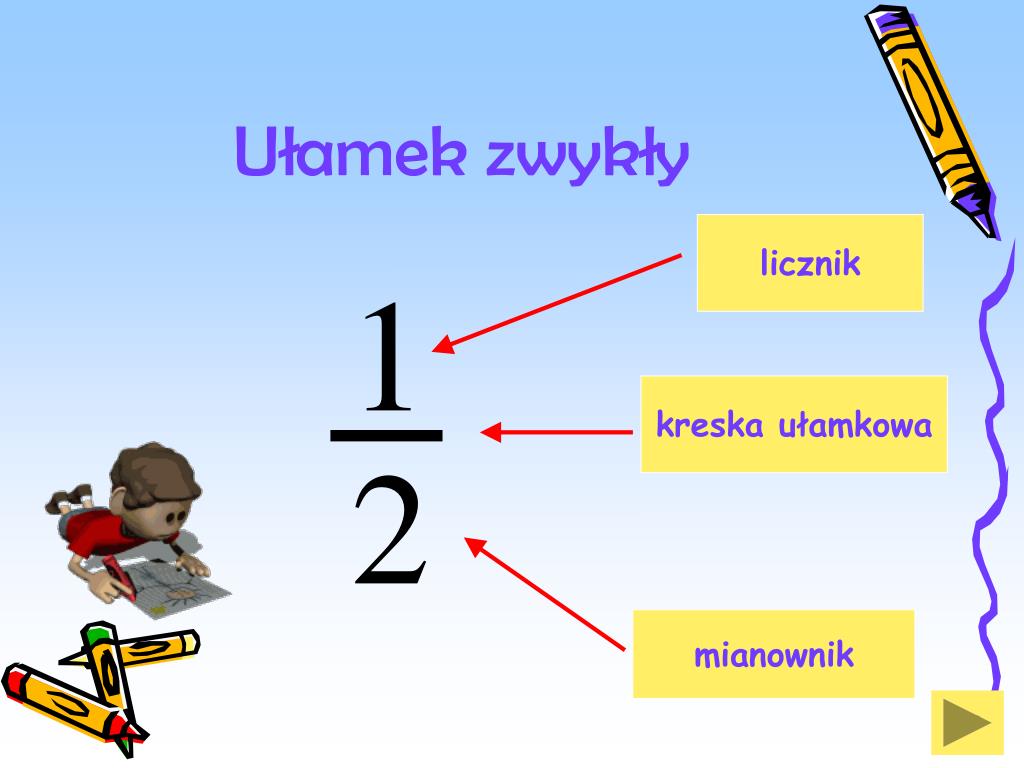
Mianownik w ułamku jest liczbą zapisaną poniżej kreski ułamkowej. Jego rola jest niezwykle prosta, ale zarazem fundamentalna: określa on, na ile równych części została podzielona całość. Innymi słowy, mianownik mówi nam, jaki jest rozmiar jednostkowej części w stosunku do całości. Przykładowo, w ułamku ½, mianownik (2) informuje nas, że całość została podzielona na dwie równe części.

Ułamek składa się z dwóch głównych części: licznika i mianownika. Licznik, znajdujący się powyżej kreski ułamkowej, wskazuje ile z tych równych części bierzemy pod uwagę. Mianownik natomiast definiuje rodzaj tych części. Razem, licznik i mianownik tworzą kompletną informację o ułamkowej reprezentacji danej wartości.

Rola Mianownika w Określaniu Wartości Ułamka

Wartość ułamka jest odwrotnie proporcjonalna do wartości mianownika, przy założeniu, że licznik pozostaje stały. Oznacza to, że im większy mianownik, tym mniejsza wartość ułamka. Dzieje się tak dlatego, że całość jest dzielona na coraz większą liczbę części, a co za tym idzie, każda pojedyncza część staje się mniejsza.

Przykładowo, porównajmy ułamki ¼ i ⅛. W pierwszym przypadku, całość została podzielona na 4 części, a my bierzemy jedną z nich. W drugim przypadku, całość została podzielona na 8 części, a my również bierzemy jedną z nich. Oczywistym jest, że ¼ jest większe od ⅛, ponieważ w pierwszym przypadku bierzemy większą część całości. To właśnie mianownik decyduje o "rozmiarze" tej części.

Mianownik a Działania na Ułamkach

Zrozumienie roli mianownika jest kluczowe przy wykonywaniu działań na ułamkach, takich jak dodawanie, odejmowanie, mnożenie i dzielenie.

Dodawanie i Odejmowanie Ułamków

Ułamki można dodawać lub odejmować tylko wtedy, gdy mają wspólny mianownik. Dzieje się tak dlatego, że tylko wtedy możemy porównywać i agregować te same "rodzaje" części całości. Jeśli ułamki nie mają wspólnego mianownika, należy je najpierw sprowadzić do wspólnego mianownika, znajdując najmniejszą wspólną wielokrotność (NWW) mianowników i przekształcając ułamki tak, aby miały tę samą wartość, ale z nowym mianownikiem.

Przykład: Chcemy dodać ułamki ½ i ¼. Ułamki te nie mają wspólnego mianownika. Najmniejszą wspólną wielokrotnością 2 i 4 jest 4. Przekształcamy ½ do postaci 2/4 (mnożąc licznik i mianownik przez 2). Teraz możemy dodać ułamki: 2/4 + ¼ = ¾.

Mnożenie i Dzielenie Ułamków

Mnożenie ułamków jest prostsze niż dodawanie i odejmowanie pod względem mianownika, ponieważ nie wymaga sprowadzania do wspólnego mianownika. Mnożymy licznik przez licznik i mianownik przez mianownik.

Dzielenie ułamków polega na pomnożeniu pierwszego ułamka przez odwrotność drugiego ułamka. Odwrotność ułamka to zamiana miejscami licznika i mianownika. Zatem, mianownik odgrywa tutaj pośrednią rolę, wpływając na to, jaką wartość uzyskamy po odwróceniu ułamka.

Specjalne Przypadki Mianownika

Istnieją pewne specyficzne przypadki dotyczące mianownika, które warto znać.

Mianownik Równy 1

Jeśli mianownik ułamka wynosi 1, to ułamek reprezentuje liczbę całkowitą. Przykładowo, 5/1 to po prostu liczba 5. Mianownik równy 1 oznacza, że całość nie została podzielona na żadne części – bierzemy całą całość.

Mianownik Równy 0

Mianownik nigdy nie może być równy 0. Dzielenie przez zero jest niedozwolone w matematyce. Ułamek z mianownikiem równym 0 jest nieokreślony. Próba obliczenia wartości takiego ułamka prowadzi do sprzeczności i nie ma sensownego wyniku.

Wyobraźmy sobie, że chcemy podzielić tort na 0 części. Jest to oczywiście niemożliwe. Nie możemy podzielić czegoś na zero części, dlatego też dzielenie przez zero jest niedefiniowalne.

Mianownik w Życiu Codziennym

Ułamki, a zatem i mianowniki, są wszechobecne w naszym życiu codziennym, choć często nie zdajemy sobie z tego sprawy. Oto kilka przykładów:

• Gotowanie i Przepisy: Przepisy kulinarne często podają proporcje składników w formie ułamków (np. ½ szklanki mąki, ¼ łyżeczki soli). Mianownik w tym przypadku informuje nas, na ile części została podzielona szklanka lub łyżeczka.
• Mierzenie Czasu: Godzina jest podzielona na 60 minut, a minuta na 60 sekund. Mówiąc, że minęła kwadrans (¼ godziny), używamy ułamka z mianownikiem 4.
• Finanse: Procenty to nic innego jak ułamki z mianownikiem 100. 50% to ½, 25% to ¼, itd. Mianownik 100 informuje nas, że całość została podzielona na 100 równych części.
• Budownictwo: Planowanie i projektowanie budynków często wymaga precyzyjnych obliczeń, w których ułamki odgrywają kluczową rolę. Mianowniki pomagają określić proporcje i wymiary elementów konstrukcyjnych.
• Dane Statystyczne: W analizie danych statystycznych często używamy ułamków do reprezentowania proporcji i udziałów. Przykładowo, możemy powiedzieć, że ¼ respondentów popiera daną opcję.

Podsumowanie

Mianownik jest fundamentalnym elementem ułamka, definiującym, na ile równych części została podzielona całość. Zrozumienie jego roli jest kluczowe dla wykonywania działań na ułamkach, rozwiązywania problemów matematycznych i interpretowania informacji przedstawionych w formie ułamkowej. Pamiętaj, że im większy mianownik, tym mniejsza wartość ułamka (przy stałym liczniku), a mianownik nigdy nie może być równy 0. Mianowniki otaczają nas w życiu codziennym, wpływając na sposób, w jaki mierzymy, planujemy i analizujemy świat wokół nas.

Zachęcamy do dalszego zgłębiania wiedzy na temat ułamków i ich zastosowań. Ćwiczenia i rozwiązywanie zadań praktycznych pomogą utrwalić zdobytą wiedzę i rozwinąć umiejętność operowania ułamkami w różnych kontekstach.