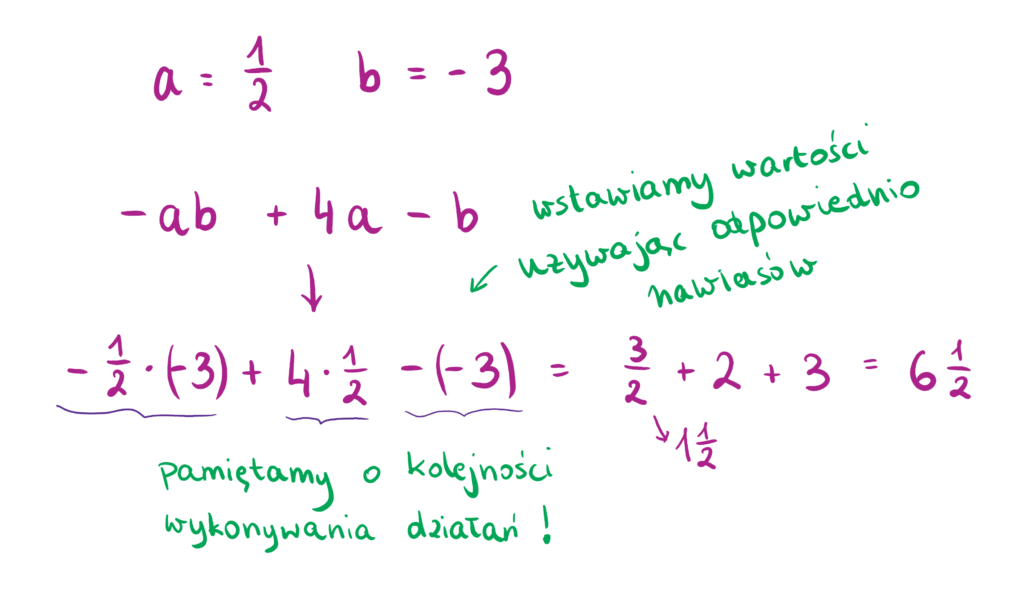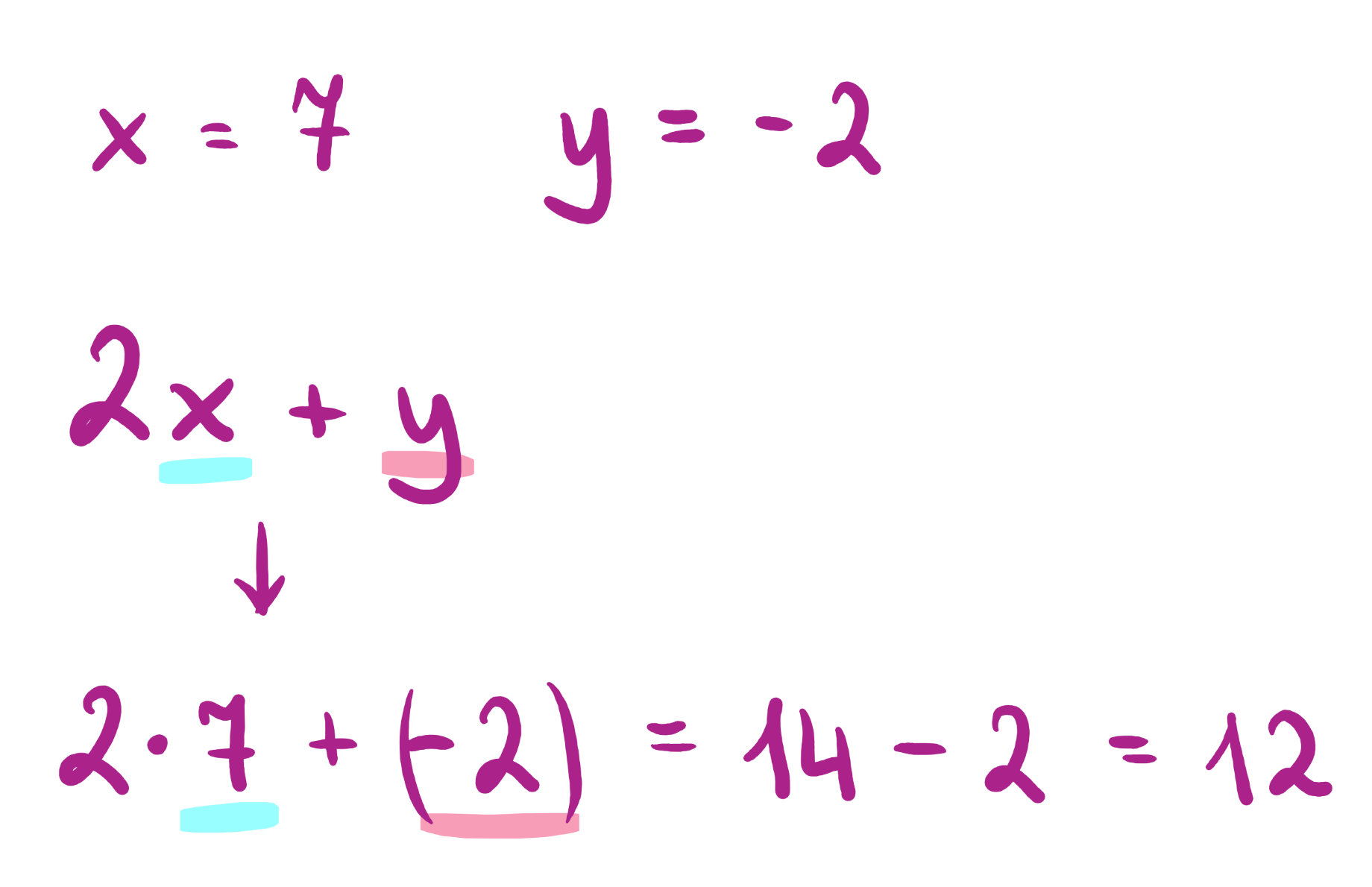Co To Jest Wyrażenie Algebraiczne

Czy kiedykolwiek patrzyłeś/aś na równanie pełne liter i liczb i czułeś/aś się zagubiony/a? Nie jesteś sam/a! Wiele osób, szczególnie na początku swojej przygody z matematyką, ma problem z zrozumieniem, czym są wyrażenia algebraiczne i do czego służą. Ten artykuł ma za zadanie rozwiać wszelkie Twoje wątpliwości i pokazać, że algebra wcale nie jest taka straszna, jak ją malują!

Czym Właściwie Jest Wyrażenie Algebraiczne?

Wyobraź sobie, że masz worek z jabłkami. Nie wiesz, ile dokładnie jabłek w nim jest, więc oznaczasz tę nieznaną liczbę literą, na przykład "x". Teraz, jeśli ktoś da Ci jeszcze trzy jabłka, możesz zapisać, ile masz jabłek łącznie jako "x + 3". To jest właśnie przykład wyrażenia algebraicznego!

Mówiąc bardziej formalnie, wyrażenie algebraiczne to kombinacja zmiennych (czyli liter, które reprezentują nieznane wartości), stałych (czyli konkretnych liczb) i operacji matematycznych (takich jak dodawanie, odejmowanie, mnożenie, dzielenie, potęgowanie i pierwiastkowanie).

Przykładami wyrażeń algebraicznych są:

• 3x + 2y - 5
• a² - 4ac
• (p + q) / 2
• √z + 7

Kluczowe Składniki Wyrażenia Algebraicznego

Aby lepiej zrozumieć, przyjrzyjmy się bliżej poszczególnym elementom:

• Zmienna: To litera (np. x, y, a, b), która reprezentuje nieznaną wartość. Może przyjmować różne wartości.
• Stała: To liczba, która ma ustaloną wartość (np. 2, 5, -10, π).
• Współczynnik: To liczba, która stoi przed zmienną i ją mnoży (np. w wyrażeniu 3x, "3" jest współczynnikiem).
• Wyrazy: To poszczególne części wyrażenia algebraicznego oddzielone znakami dodawania lub odejmowania (np. w wyrażeniu 3x + 2y - 5, wyrazy to 3x, 2y i -5).
• Operatory: To znaki działań matematycznych (np. +, -, *, /, ^, √).

Po Co Używamy Wyrażeń Algebraicznych?

Wyrażenia algebraiczne są niezwykle przydatne, ponieważ pozwalają nam wyrażać ogólne zależności i rozwiązywać problemy, w których niektóre wartości są nieznane. Pomyśl o tym jak o języku, który pozwala nam opisywać świat za pomocą matematyki.

Oto kilka przykładów zastosowań:

• Fizyka: Wyrażenia algebraiczne są używane do opisywania ruchów, sił i energii. Na przykład, wzór na energię kinetyczną to E = 1/2 * mv², gdzie E to energia kinetyczna, m to masa, a v to prędkość.
• Inżynieria: Inżynierowie używają wyrażeń algebraicznych do projektowania mostów, budynków i innych konstrukcji.
• Ekonomia: Ekonomiści używają wyrażeń algebraicznych do modelowania rynków i przewidywania trendów.
• Informatyka: Programiści używają wyrażeń algebraicznych do pisania algorytmów i tworzenia oprogramowania.
• Życie codzienne: Nawet nie zdając sobie z tego sprawy, używamy wyrażeń algebraicznych w codziennych sytuacjach, np. przy obliczaniu kosztów zakupów, planowaniu budżetu lub gotowaniu. Załóżmy, że chcesz kupić 3 jabłka po x złotych za sztukę i 2 gruszki po y złotych za sztukę. Całkowity koszt to 3x + 2y.

Według raportu National Mathematics Advisory Panel, "algebra is the gateway to advanced mathematics". Zrozumienie wyrażeń algebraicznych jest więc kluczowe dla dalszego rozwoju w matematyce i naukach pokrewnych.

Jak Pracować z Wyrażeniami Algebraicznymi?

Opanowanie operacji na wyrażeniach algebraicznych wymaga praktyki. Oto kilka podstawowych operacji:

1. Upraszczanie Wyrażeń

Upraszczanie wyrażeń polega na zredukowaniu ich do najprostszej postaci poprzez łączenie wyrazów podobnych i wykonywanie działań. Wyrazy podobne to takie, które mają tę samą zmienną podniesioną do tej samej potęgi (np. 3x i -5x są wyrazami podobnymi, ale 3x i 3x² już nie).

Przykład:

Uprość wyrażenie: 5x + 2y - 3x + 4y

Rozwiązanie: (5x - 3x) + (2y + 4y) = 2x + 6y

2. Dodawanie i Odejmowanie Wyrażeń

Dodawanie i odejmowanie wyrażeń algebraicznych polega na łączeniu wyrazów podobnych w obu wyrażeniach.

Przykład:

Dodaj wyrażenia: (2a + 3b) + (5a - b)

Rozwiązanie: 2a + 3b + 5a - b = (2a + 5a) + (3b - b) = 7a + 2b

3. Mnożenie Wyrażeń

Mnożenie wyrażeń algebraicznych wymaga zastosowania prawa rozdzielności. Oznacza to, że każdy wyraz w jednym wyrażeniu musi być pomnożony przez każdy wyraz w drugim wyrażeniu.

Przykład:

Pomnóż wyrażenia: (x + 2) * (x - 3)

Rozwiązanie: x * (x - 3) + 2 * (x - 3) = x² - 3x + 2x - 6 = x² - x - 6

4. Dzielenie Wyrażeń

Dzielenie wyrażeń algebraicznych jest bardziej skomplikowane i często wymaga znajomości rozkładania na czynniki lub dzielenia wielomianów.

Praktyczne Wskazówki i Ćwiczenia

Aby lepiej zrozumieć wyrażenia algebraiczne, warto regularnie ćwiczyć. Oto kilka wskazówek:

• Zacznij od prostych przykładów: Nie rzucaj się od razu na trudne zadania. Zacznij od upraszczania prostych wyrażeń, a następnie stopniowo zwiększaj poziom trudności.
• Używaj zasobów online: Istnieje wiele stron internetowych i aplikacji, które oferują ćwiczenia i samouczki z algebry.
• Szukaj pomocy: Jeśli masz trudności, nie bój się pytać nauczyciela, korepetytora lub znajomych, którzy dobrze radzą sobie z matematyką.
• Rób notatki: Zapisuj ważne definicje, wzory i przykłady. Pomoże Ci to w zapamiętywaniu i powtarzaniu materiału.
• Pracuj w grupach: Wspólna praca z innymi może być bardzo motywująca i pomóc Ci w zrozumieniu trudnych zagadnień.
• Stosuj algebrę w życiu codziennym: Spróbuj wykorzystywać wyrażenia algebraiczne do rozwiązywania problemów, które napotykasz w życiu codziennym. Pomoże Ci to zrozumieć praktyczne zastosowanie algebry.

Przykładowe ćwiczenia:

1. Uprość wyrażenie: 7a - 3b + 2a + 5b - a
2. Dodaj wyrażenia: (4x² - 2x + 1) + (x² + 3x - 5)
3. Pomnóż wyrażenia: (y + 4) * (y - 1)

Podsumowanie

Mam nadzieję, że ten artykuł pomógł Ci zrozumieć, czym są wyrażenia algebraiczne i jak z nimi pracować. Pamiętaj, że kluczem do sukcesu jest regularna praktyka i cierpliwość. Nie zrażaj się trudnościami i nie bój się pytać o pomoc. Algebra to potężne narzędzie, które może otworzyć Ci drzwi do wielu fascynujących dziedzin nauki i technologii. Zrozumienie jej podstaw to inwestycja, która z pewnością się opłaci!

Powodzenia w nauce!