Co To Jest Ułamek Zwykły

Czy kiedykolwiek dzieliłeś pizzę ze znajomymi i zastanawiałeś się, jak sprawiedliwie podzielić każdą część? A może piekąc ciasto, musiałeś odmierzyć połowę szklanki mąki? W takich sytuacjach intuicyjnie korzystamy z ułamków. I choć dla niektórych matematyka, w tym ułamki, wydaje się skomplikowana, w rzeczywistości są one niezwykle przydatne w codziennym życiu. Rozumienie, czym jest ułamek zwykły, to pierwszy krok do okiełznania tego potężnego narzędzia. Postaram się to wytłumaczyć w sposób jasny i przystępny.

Co to właściwie jest ułamek zwykły?

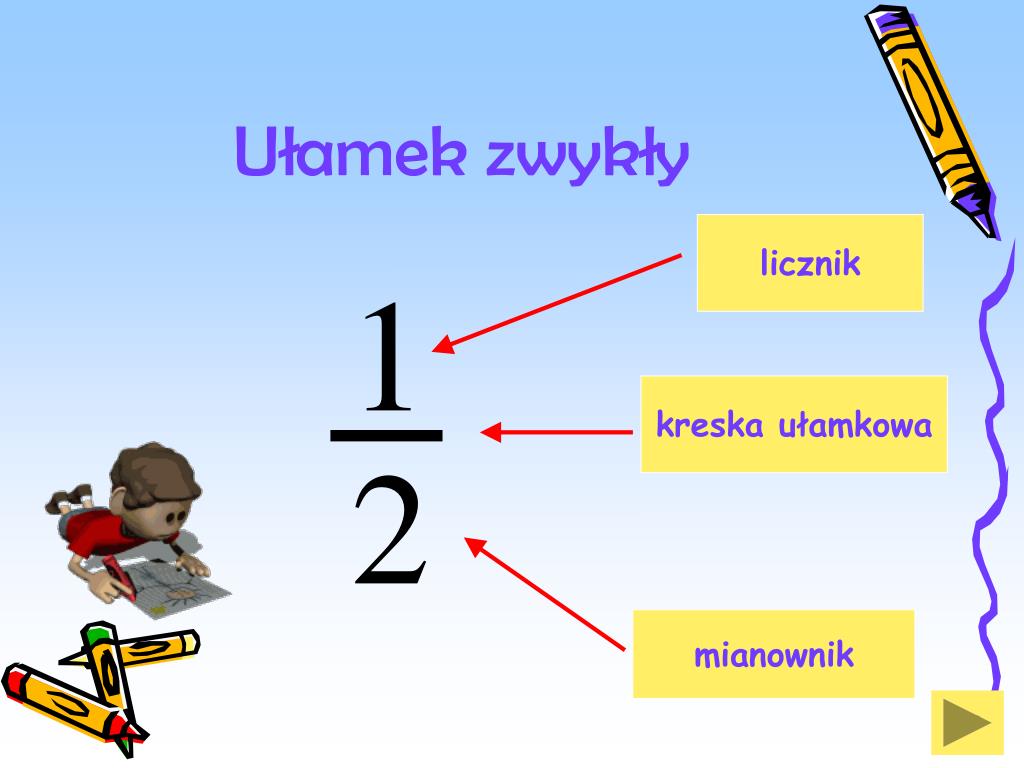
Ułamek zwykły to nic innego jak sposób na przedstawienie części całości. Wyobraź sobie, że masz jabłko i dzielisz je na cztery równe części. Każda z tych części to ułamek jabłka. Ułamek zwykły zapisujemy za pomocą dwóch liczb oddzielonych kreską ułamkową. Liczba nad kreską nazywa się licznikiem, a liczba pod kreską to mianownik.

Licznik mówi nam, ile części całości posiadamy. W naszym przykładzie, jeśli zjesz jedną ćwiartkę jabłka, licznik wynosi 1. Mianownik informuje nas, na ile równych części podzielona została całość. W tym przypadku, mianownik to 4, ponieważ jabłko zostało podzielone na cztery części. Zatem, zjedzenie jednej ćwiartki jabłka zapiszemy jako ułamek 1/4 (czytamy: jedna czwarta).

Prosty, prawda? Ale skąd tak naprawdę wzięła się potrzeba używania ułamków?

Dlaczego potrzebujemy ułamków?

Ułamki pozwalają nam wyrazić ilości, które nie są liczbami całkowitymi. Bez nich mielibyśmy poważny problem z opisaniem wielu sytuacji. Pomyśl o:

Podziale zasobów: Jak sprawiedliwie podzielić kawałek ciasta między trójkę dzieci? Ułamki (1/3 dla każdego) dają nam precyzyjne rozwiązanie.
Odmierzaniu składników: Przepisy kulinarne często wymagają użycia np. 1/2 szklanki cukru lub 3/4 łyżeczki soli.
Mierzeniu długości: Jeśli masz kawałek materiału o długości 2,5 metra, ułamek (0,5, który można zapisać jako 1/2) pozwala dokładnie opisać tę wartość.
Wyrażaniu prawdopodobieństwa: Jeśli rzucasz monetą, prawdopodobieństwo wyrzucenia orła wynosi 1/2.

Bez ułamków wiele z tych czynności stałoby się trudne lub wręcz niemożliwe. Ułamki są więc niezbędnym narzędziem w matematyce i naszym codziennym życiu.

Różne rodzaje ułamków zwykłych

Ułamki zwykłe możemy podzielić na kilka kategorii, w zależności od relacji między licznikiem a mianownikiem:

Ułamki właściwe: To takie ułamki, w których licznik jest mniejszy od mianownika. Reprezentują one część całości mniejszą niż 1. Przykład: 2/5, 3/8, 7/10.
Ułamki niewłaściwe: W tych ułamkach licznik jest większy lub równy mianownikowi. Reprezentują one całość lub więcej niż całość. Przykład: 5/5, 7/3, 10/4.
Liczby mieszane: To połączenie liczby całkowitej i ułamka właściwego. Reprezentują one ilości większe niż 1. Przykład: 1 1/2 (czytaj: jeden i jedna druga), 2 3/4 (czytaj: dwa i trzy czwarte).

Ułamki niewłaściwe i liczby mieszane możemy zamieniać między sobą. Na przykład, ułamek niewłaściwy 7/3 możemy zapisać jako liczbę mieszaną 2 1/3 (ponieważ 7 podzielone przez 3 daje 2 reszty 1).

Upraszczanie ułamków: Po co to robimy?

Upraszczanie ułamków (czyli skracanie) polega na podzieleniu licznika i mianownika przez ten sam liczbę, aż nie da się już ich bardziej uprościć. Ma to na celu przedstawienie ułamka w najprostszej postaci. Na przykład, ułamek 4/8 możemy uprościć dzieląc licznik i mianownik przez 4, otrzymując 1/2. Ułamek 4/8 i 1/2 reprezentują tę samą wartość, ale 1/2 jest prostszy i łatwiejszy do zrozumienia.

Dlaczego to takie ważne? Uproszczone ułamki są:

Łatwiejsze do porównania: Szybciej zorientujesz się, który ułamek jest większy, jeśli oba są uproszczone.
Bardziej czytelne: Uproszczony ułamek jest po prostu łatwiejszy do odczytania i zrozumienia.
Niezbędne w dalszych obliczeniach: W wielu operacjach matematycznych, praca z uproszczonymi ułamkami jest znacznie łatwiejsza i zmniejsza ryzyko pomyłek.

Ułamki w praktyce: Przykłady z życia

Ułamki, jak już wspomnieliśmy, otaczają nas wszędzie. Przyjrzyjmy się kilku konkretnym przykładom:

Gotowanie i pieczenie: Większość przepisów wymaga użycia ułamków do odmierzania składników. Na przykład, przepis na ciasto może wymagać 1/2 szklanki mleka, 3/4 łyżeczki proszku do pieczenia i 1 1/4 szklanki mąki.
Zakupy: Często widzimy promocje typu "2 w cenie 1 1/2". Ułamki pomagają nam zrozumieć, ile tak naprawdę zaoszczędzamy.
Podróże: Planując podróż, możemy analizować mapy, które często używają skali wyrażonej za pomocą ułamka (np. 1:100 000, co oznacza, że 1 cm na mapie odpowiada 100 000 cm w rzeczywistości).
Sport: W wielu dyscyplinach sportowych używa się ułamków do pomiaru czasu, odległości lub innych parametrów. Na przykład, w biegu na 100 metrów czas mierzony jest z dokładnością do setnych sekundy (np. 9,91 sekundy, co można zapisać jako 9 91/100 sekundy).

To tylko kilka przykładów. Ułamki są obecne w wielu aspektach naszego życia, choć często nie zdajemy sobie z tego sprawy.

Obawy i kontrargumenty: Czy ułamki są naprawdę trudne?

Wiele osób obawia się ułamków, postrzegając je jako trudny i abstrakcyjny koncept. Często słyszy się narzekania, że "matematyka to nie dla mnie" albo "nigdy nie zrozumiem ułamków". Jednak te obawy często wynikają z braku odpowiedniego podejścia do tematu.

Kontrargument: Ułamki wcale nie muszą być trudne! Kluczem jest zrozumienie podstawowych zasad i praktyczne ćwiczenia. Używanie wizualnych pomocy, takich jak rysunki czy modele, może bardzo pomóc w zrozumieniu idei ułamka. Ważne jest również, aby łączyć ułamki z realnymi sytuacjami z życia codziennego. Kiedy widzimy, jak ułamki działają w praktyce, łatwiej nam je zrozumieć.

Pamiętaj, że każdy może nauczyć się ułamków! Wymaga to tylko trochę cierpliwości, dobrego podejścia i chęci do nauki.

Rozwiązania i dalsze kroki

Jeśli chcesz lepiej zrozumieć ułamki zwykłe, oto kilka propozycji:

Ćwicz regularnie: Im więcej będziesz ćwiczył, tym lepiej zrozumiesz zasady rządzące ułamkami. Możesz korzystać z podręczników, ćwiczeń online lub aplikacji do nauki matematyki.
Używaj wizualizacji: Rysuj koła, kwadraty lub inne kształty i dziel je na równe części, aby zobaczyć, jak wyglądają ułamki.
Szukaj przykładów w życiu codziennym: Zwracaj uwagę na sytuacje, w których używane są ułamki. Na przykład, kiedy pieczesz ciasto, zastanów się, jak ułamki pomagają Ci odmierzyć składniki.
Nie bój się pytać: Jeśli masz wątpliwości, pytaj nauczyciela, kolegów lub szukaj odpowiedzi w internecie.
Wykorzystaj gry edukacyjne: Istnieje wiele gier edukacyjnych, które w zabawny sposób uczą o ułamkach.

Pamiętaj, że nauka matematyki to proces, który wymaga czasu i wysiłku. Nie zrażaj się początkowymi trudnościami. Z każdym kolejnym krokiem będziesz coraz bliżej celu.

Ułamki zwykłe to potężne narzędzie, które może ułatwić Ci życie w wielu sytuacjach. Zrozumienie ich zasad otwiera drzwi do dalszej nauki matematyki i rozwija umiejętność logicznego myślenia.

Teraz, po przeczytaniu tego artykułu, zastanów się, w jakich sytuacjach w Twoim życiu ułamki mogłyby Ci pomóc. Czy potrafisz dostrzec ich obecność w codziennych czynnościach? Spróbuj przeanalizować to przez najbliższy tydzień i zobacz, jak zmienia się Twoje postrzeganie matematyki!