Co To Jest Równanie Sprzeczne

Zdarzyło Ci się kiedyś próbować rozwiązać zadanie, które od początku wydawało się niemożliwe? Zadanie, w którym wszystko przeczy samo sobie i prowadzi do absurdalnych wniosków? W matematyce, takie zadania kryją się pod nazwą równań sprzecznych. W tym artykule przyjrzymy się im bliżej, abyś mógł/mogła je łatwo rozpoznawać i unikać frustracji podczas rozwiązywania problemów.

Ten artykuł jest skierowany do uczniów szkół średnich, studentów rozpoczynających studia z elementami matematyki, a także do wszystkich, którzy chcą odświeżyć swoją wiedzę i zrozumieć, czym są równania sprzeczne oraz jak je identyfikować.

Czym jest Równanie Sprzeczne?

Najprościej mówiąc, równanie sprzeczne to takie równanie, które nie ma żadnego rozwiązania. Niezależnie od tego, jaką wartość podstawimy za niewiadomą (zazwyczaj oznaczaną jako 'x'), równanie nigdy nie będzie prawdziwe. Wynika to z wewnętrznej sprzeczności w jego strukturze. Inaczej mówiąc, to równanie, które prowadzi do fałszywego stwierdzenia dla każdej możliwej wartości niewiadomej.

Charakterystyczne Cechy Równania Sprzecznego:

Brak rozwiązań: To podstawowa definicja – nie istnieje żadna wartość niewiadomej, która spełniałaby równanie.
Prowadzi do sprzeczności: Przekształcenia równania prowadzą do absurdalnego wyniku, np. 0 = 1, -5 = 2, czy x = x + 1.
Niespójność: Równanie zawiera w sobie sprzeczne założenia, które uniemożliwiają znalezienie rozwiązania.

Przykłady Równań Sprzecznych

Aby lepiej zrozumieć ideę równań sprzecznych, przyjrzyjmy się kilku przykładom:

Przykład 1: Proste Równanie Liniowe

Rozważmy równanie: x + 2 = x + 5

Próbując je rozwiązać, możemy odjąć 'x' od obu stron:

x + 2 - x = x + 5 - x

2 = 5

Otrzymaliśmy stwierdzenie, które jest oczywiście fałszywe. 2 nigdy nie będzie równe 5. Oznacza to, że równanie x + 2 = x + 5 jest równaniem sprzecznym. Nie ma żadnej wartości 'x', która by je spełniała.

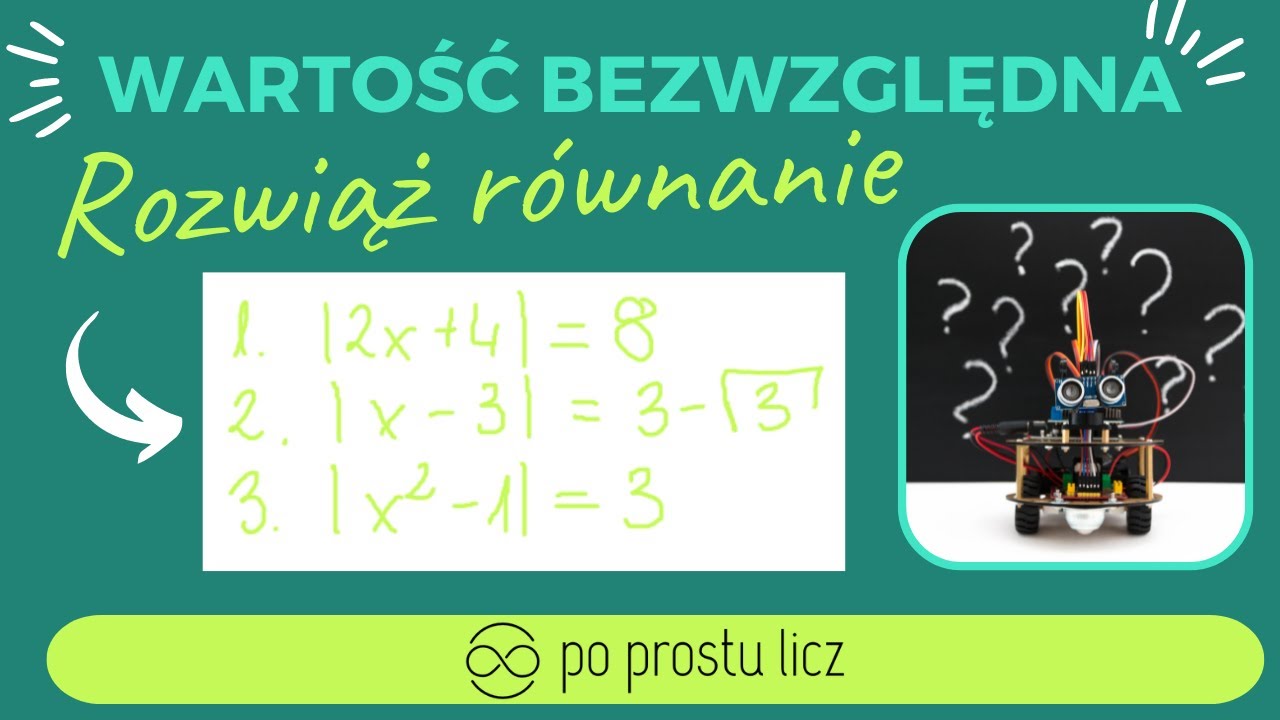
Przykład 2: Równanie z Wartością Bezwzględną

Rozważmy równanie: |x| = -3

Wartość bezwzględna liczby to jej odległość od zera na osi liczbowej. Z definicji, wartość bezwzględna jest zawsze nieujemna (większa lub równa zero). Zatem, |x| nigdy nie może być równe -3. To równanie również jest sprzeczne.

Przykład 3: Równanie z Ułamkami

Rozważmy równanie: 1/x = 0

Żaden ułamek o liczniku 1 nie może być równy zero. Niezależnie od tego, jaką wartość podstawimy za 'x' (różną od zera, bo dzielenie przez zero jest niedozwolone), wartość 1/x nigdy nie wyniesie 0. Zatem to równanie jest równaniem sprzecznym.

Przykład 4: Równanie Kwadratowe

Rozważmy równanie kwadratowe: x² + 1 = 0

Próbując je rozwiązać, możemy przenieść 1 na drugą stronę równania:

x² = -1

Kwadrat dowolnej liczby rzeczywistej jest zawsze nieujemny (większy lub równy zero). Nie istnieje żadna liczba rzeczywista, której kwadrat byłby równy -1. Dlatego, jeśli rozpatrujemy rozwiązania w zbiorze liczb rzeczywistych, to równanie jest sprzeczne. (Posiada rozwiązania w zbiorze liczb zespolonych, ale to już inna historia!).

Jak Rozpoznać Równanie Sprzeczne?

Rozpoznawanie równań sprzecznych wymaga pewnej wprawy i zrozumienia podstawowych zasad matematyki. Oto kilka wskazówek, które mogą Ci pomóc:

Uważnie analizuj równanie: Zanim zaczniesz przekształcać równanie, przyjrzyj się mu uważnie. Czy dostrzegasz jakieś potencjalne sprzeczności? Czy któraś część równania wydaje się niemożliwa do spełnienia?
Wykonuj przekształcenia algebraiczne: Spróbuj uprościć równanie, stosując znane Ci metody algebraiczne (dodawanie, odejmowanie, mnożenie, dzielenie, podnoszenie do potęgi, pierwiastkowanie, itp.). Obserwuj, czy przekształcenia prowadzą do absurdalnych wniosków.
Zwróć uwagę na własności liczb: Pamiętaj o podstawowych własnościach liczb rzeczywistych, takich jak nieujemność wartości bezwzględnej, nieujemność kwadratu liczby, czy niemożliwość dzielenia przez zero.
Sprawdzaj rozwiązania: Jeśli uda Ci się znaleźć potencjalne rozwiązanie, zawsze sprawdź, czy rzeczywiście spełnia ono równanie. W przypadku równań sprzecznych, sprawdzenie zawsze ujawni sprzeczność.
Szukaj wzorów skróconego mnożenia: Czasami, równanie może być ukryte w bardziej złożonej formie. Rozpoznanie wzoru skróconego mnożenia może pomóc w uproszczeniu równania i ujawnieniu jego sprzeczności.

Dlaczego Warto Rozumieć Równania Sprzeczne?

Zrozumienie koncepcji równań sprzecznych ma wiele praktycznych korzyści:

Oszczędność czasu: Rozpoznanie równania sprzecznego na początku rozwiązywania pozwala uniknąć niepotrzebnej pracy i frustracji. Zamiast tracić czas na szukanie nieistniejącego rozwiązania, możesz od razu stwierdzić, że równanie jest sprzeczne.
Poprawa umiejętności rozwiązywania problemów: Rozwiązywanie równań (w tym rozpoznawanie sprzecznych) rozwija umiejętność logicznego myślenia, analizowania i wyciągania wniosków.
Lepsze zrozumienie matematyki: Zrozumienie koncepcji równań sprzecznych pogłębia ogólną wiedzę matematyczną i pozwala lepiej zrozumieć relacje między różnymi elementami matematyki.
Unikanie błędów: Umiejętność rozpoznawania równań sprzecznych pomaga unikać błędów w bardziej złożonych problemach, gdzie równanie sprzeczne może być tylko częścią większej całości.

Równania Sprzeczne w Praktyce

Równania sprzeczne, choć same w sobie nie posiadają rozwiązań, mogą pojawiać się w różnych kontekstach matematycznych i praktycznych:

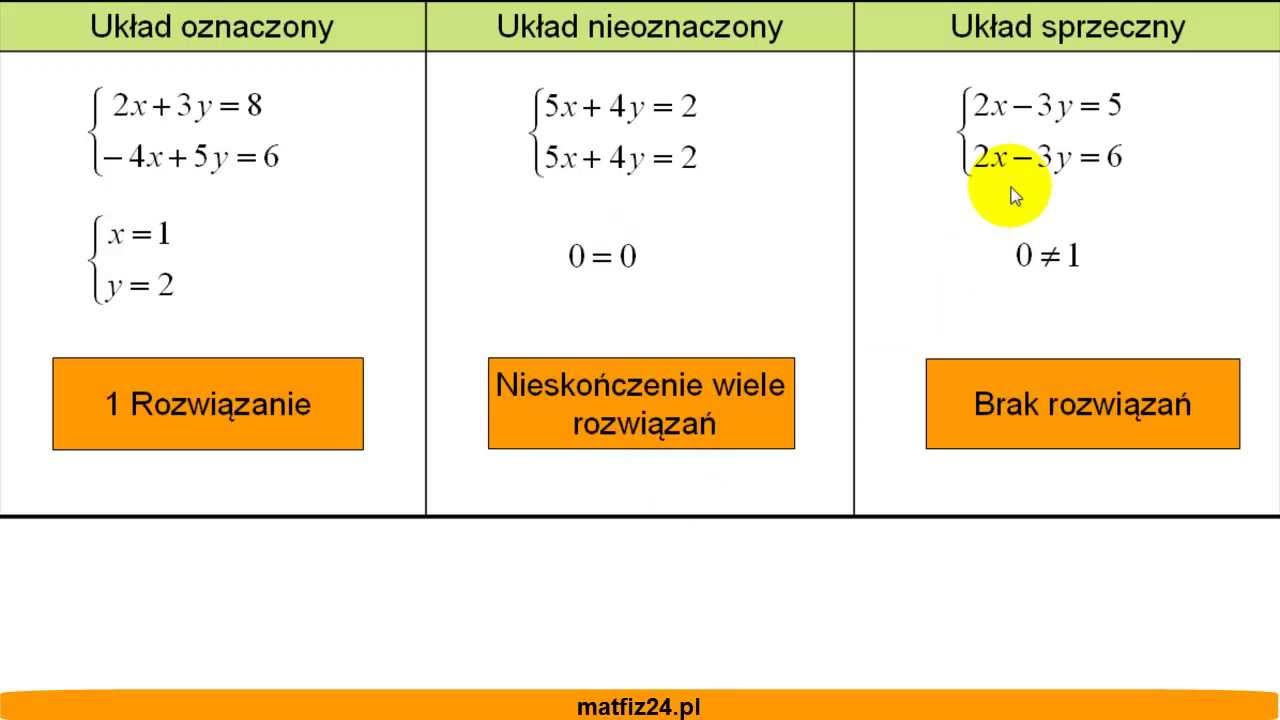
Układy równań: W układach równań, sprzeczność jednego z równań może oznaczać, że cały układ nie ma rozwiązania.
Optymalizacja: W problemach optymalizacyjnych, ograniczenia opisane równaniami sprzecznymi mogą wskazywać, że nie istnieje dopuszczalne rozwiązanie.
Modelowanie matematyczne: Jeśli model matematyczny prowadzi do równania sprzecznego, może to oznaczać, że model jest nieprawidłowy lub wymaga modyfikacji.
Logika: W logice matematycznej, sprzeczność w zbiorze aksjomatów oznacza, że system jest niespójny.

Podsumowanie

Równanie sprzeczne to równanie, które nie ma żadnego rozwiązania, ponieważ prowadzi do sprzeczności logicznej. Rozpoznawanie równań sprzecznych jest ważną umiejętnością, która pozwala oszczędzić czas, unikać błędów i lepiej zrozumieć matematykę. Pamiętaj o uważnej analizie równania, wykonywaniu przekształceń algebraicznych i sprawdzaniu potencjalnych rozwiązań. Miej na uwadze własności liczb i poszukuj wzorów skróconego mnożenia. Dzięki temu z łatwością rozpoznasz równanie sprzeczne i unikniesz frustracji podczas rozwiązywania problemów matematycznych. Mam nadzieję, że ten artykuł pomógł Ci zrozumieć istotę równań sprzecznych i jak je rozpoznawać. Powodzenia w dalszej nauce!