Co To Jest Pierwiastek Matematyka

Czy kiedykolwiek zastanawiałeś się, co tak naprawdę oznacza ten dziwny symbol √, który widzisz w podręcznikach do matematyki, a może nawet sporadycznie w życiu codziennym? Może wydaje się skomplikowany i odległy, ale w gruncie rzeczy pierwiastek to całkiem proste i użyteczne narzędzie. Jeśli kiedykolwiek czułeś się zagubiony, próbując zrozumieć, czym jest pierwiastek, ten artykuł jest dla Ciebie. Postaramy się wyjaśnić to zagadnienie w sposób jasny i przystępny.

Czym Właściwie Jest Pierwiastek?

Najprościej mówiąc, pierwiastek to operacja matematyczna, która znajduje liczbę, która po pomnożeniu przez samą siebie (w przypadku pierwiastka kwadratowego) daje liczbę, z której wyciągamy pierwiastek. Brzmi skomplikowanie? Spokojnie, rozłóżmy to na czynniki pierwsze.

Wyobraź sobie, że masz kwadrat o polu 9. Jakiej długości jest bok tego kwadratu? Odpowiedź to 3, ponieważ 3 * 3 = 9. W matematyce, mówimy, że pierwiastek kwadratowy z 9 to 3. Zapisujemy to jako √9 = 3.

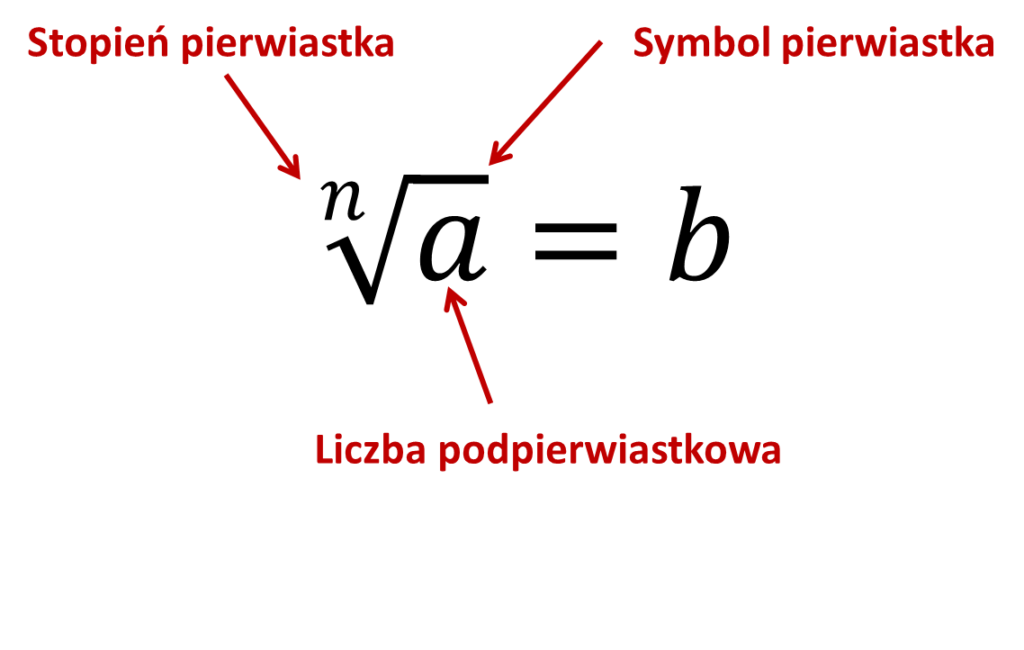
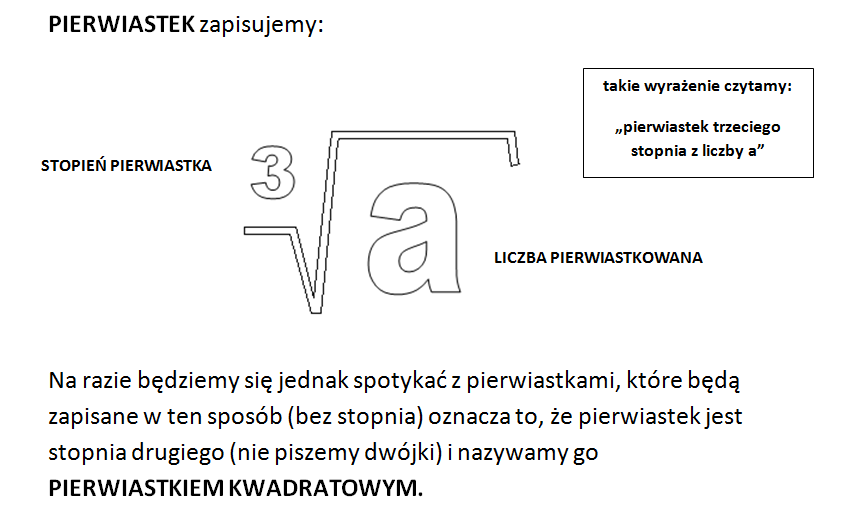
Formalnie, pierwiastek n-tego stopnia z liczby x, to taka liczba y, że yⁿ = x. Czyli √[n]{x} = y ⇔ yⁿ = x.

Ważne! Pierwiastek kwadratowy (n=2) jest najczęściej używany, dlatego często pomija się zapis indeksu pierwiastka - czyli zamiast √[2]{x} piszemy po prostu √{x}.

Rodzaje Pierwiastków

Najczęściej spotykamy się z pierwiastkiem kwadratowym (√), ale istnieją również inne rodzaje pierwiastków, np.:

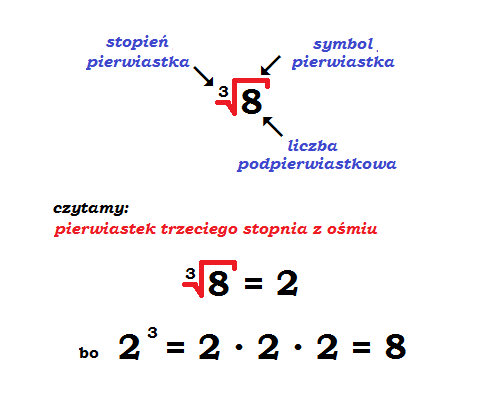
Pierwiastek sześcienny (∛): Znajduje liczbę, która pomnożona przez samą siebie trzy razy daje liczbę, z której wyciągamy pierwiastek. Na przykład, ∛8 = 2, ponieważ 2 * 2 * 2 = 8.
Pierwiastek czwartego stopnia (√[4]): Znajduje liczbę, która pomnożona przez samą siebie cztery razy daje liczbę, z której wyciągamy pierwiastek. Na przykład, √[4]{16} = 2, ponieważ 2 * 2 * 2 * 2 = 16.
Pierwiastek n-tego stopnia (√[n]): Uogólnienie powyższych przykładów.

Praktyczne Zastosowania Pierwiastków

Pierwiastki nie są tylko abstrakcyjnym pojęciem matematycznym. Mają mnóstwo zastosowań w życiu codziennym, nauce i technologii. Oto kilka przykładów:

Geometria: Obliczanie długości boków kwadratów, objętości sfer, przekątnych prostokątów (twierdzenie Pitagorasa).
Fizyka: Obliczanie prędkości, energii kinetycznej, przyspieszenia.
Informatyka: Algorytmy graficzne, kompresja danych, kryptografia.
Finanse: Obliczanie stóp procentowych, analizy ryzyka.
Budownictwo: Obliczanie wymiarów konstrukcji, stabilności budynków.

Przykład z życia: Załóżmy, że chcesz zbudować kwadratowy ogródek o powierzchni 25 metrów kwadratowych. Jak długi powinien być bok tego ogródka? Używamy pierwiastka kwadratowego: √25 = 5. Zatem bok ogródka powinien mieć długość 5 metrów.

Jak Obliczać Pierwiastki?

Istnieje kilka sposobów na obliczanie pierwiastków:

Metoda "na piechotę": Dla małych liczb można zgadywać i sprawdzać, jaka liczba po pomnożeniu przez samą siebie da wynik. To dobra metoda na początek, żeby zrozumieć koncepcję.
Tablice matematyczne: Dawniej powszechnie używane, zawierają wartości pierwiastków dla różnych liczb.
Kalkulatory: Najprostszy i najszybszy sposób, szczególnie dla bardziej skomplikowanych liczb. Większość kalkulatorów naukowych ma funkcję obliczania pierwiastka kwadratowego, a niektóre nawet pierwiastków wyższych stopni.
Oprogramowanie matematyczne: Programy takie jak Mathcad, Mathematica czy MATLAB oferują zaawansowane funkcje obliczania pierwiastków i innych operacji matematycznych.
Algorytmy iteracyjne: W informatyce stosuje się specjalne algorytmy, np. metoda Newtona-Raphsona, do przybliżonego obliczania pierwiastków, szczególnie gdy nie można znaleźć dokładnego rozwiązania analitycznego.

Kilka Praktycznych Wskazówek

Zapamiętaj kwadraty małych liczb: Znajomość kwadratów liczb od 1 do 10 (1, 4, 9, 16, 25, 36, 49, 64, 81, 100) znacznie ułatwi szacowanie pierwiastków.

Szacuj wartość pierwiastka: Zanim użyjesz kalkulatora, spróbuj oszacować wartość pierwiastka. Na przykład, √50 leży pomiędzy √49 = 7 a √64 = 8, więc wiemy, że wynik będzie gdzieś pomiędzy 7 a 8.

Używaj kalkulatora z głową: Kalkulatory są świetne, ale ważne jest, aby rozumieć, co robisz. Zwróć uwagę na kolejność wykonywania działań i upewnij się, że wprowadzasz poprawne dane.

Pierwiastki w Kontekście Historycznym

Pojęcie pierwiastka nie jest nowe. Już starożytni Egipcjanie i Babilończycy używali pierwiastków do rozwiązywania problemów geometrycznych i astronomicznych. Symbol pierwiastka (√) ewoluował na przestrzeni wieków, a jego obecna forma ustaliła się w XVII wieku.

Według "A History of Mathematical Notations" autorstwa Floriana Cajoriego, symbol pierwiastka (√) pochodzi od litery "r", oznaczającej łacińskie słowo "radix", czyli "korzeń". Stopniowo litera ta uległa przekształceniom, aż przybrała obecną formę.

Częste Błędy i Pułapki

Podczas pracy z pierwiastkami łatwo o pomyłki. Oto kilka częstych błędów, na które warto uważać:

Pierwiastek z liczby ujemnej: W dziedzinie liczb rzeczywistych nie można wyciągnąć pierwiastka kwadratowego z liczby ujemnej. Wynik jest liczbą zespoloną. (Np. √-1 = i, gdzie i to jednostka urojona).
Błędne upraszczanie wyrażeń: Pamiętaj o kolejności wykonywania działań i nie upraszczaj wyrażeń pochopnie. Np. √(a + b) ≠ √a + √b
Zapominanie o wartości bezwzględnej: Podczas wyciągania pierwiastka kwadratowego z kwadratu zmiennej, należy pamiętać o wartości bezwzględnej: √(x²) = |x|.

Podsumowanie

Pierwiastek to ważna i wszechstronna operacja matematyczna, która znajduje zastosowanie w wielu dziedzinach życia. Mimo że na początku może wydawać się skomplikowany, po zrozumieniu podstawowych zasad staje się prostym i użytecznym narzędziem.

Pamiętaj, że praktyka czyni mistrza. Ćwicz obliczanie pierwiastków, rozwiązuj zadania i eksperymentuj, a szybko zdobędziesz wprawę i zrozumienie tego zagadnienia. Nie zrażaj się trudnościami – każdy kiedyś zaczynał. A teraz, spróbuj rozwiązać kilka prostych przykładów i zobacz, jak dobrze sobie radzisz! Powodzenia!