Co To Jest Liczba Wymierna

Świat matematyki jest pełen liczb o różnych właściwościach i zastosowaniach. Jednym z fundamentalnych pojęć jest liczba wymierna. Na pierwszy rzut oka może wydawać się abstrakcyjne, ale liczby wymierne otaczają nas w życiu codziennym, stanowiąc podstawę wielu obliczeń i pomiarów.

Definicja Liczby Wymiernej

Liczba wymierna to każda liczba, którą można wyrazić jako iloraz dwóch liczb całkowitych, gdzie mianownik jest różny od zera. Inaczej mówiąc, liczba a jest wymierna, jeśli można ją zapisać w postaci p/q, gdzie p i q są liczbami całkowitymi, a q ≠ 0.

Przykłady liczb wymiernych:

2/3
-5/7
1/2
5 (bo można zapisać jako 5/1)
0 (bo można zapisać jako 0/1)
-3 (bo można zapisać jako -3/1)
0.5 (bo można zapisać jako 1/2)

Dlaczego mianownik nie może być zerem?

Dzielenie przez zero jest w matematyce niezdefiniowane. Wyobraźmy sobie, że próbujemy podzielić liczbę 5 przez 0. Oznaczałoby to znalezienie takiej liczby, która pomnożona przez 0 da nam 5. Nie ma takiej liczby, ponieważ każda liczba pomnożona przez 0 daje 0. Zatem dzielenie przez zero prowadzi do sprzeczności i dlatego jest zabronione.

Reprezentacje Liczb Wymiernych

Liczby wymierne można przedstawiać na kilka sposobów:

Ułamki zwykłe: Tak jak już wspomniano, podstawowa forma zapisu to p/q. Ważne jest, że ułamek może być skracalny, czyli licznik i mianownik mają wspólny dzielnik większy od 1. Przykład: 4/6 można skrócić do 2/3.
Ułamki dziesiętne: Każda liczba wymierna może być przedstawiona jako ułamek dziesiętny, który jest skończony lub nieskończony okresowy.

Ułamki Dziesiętne Skończone i Nieskończone Okresowe

Ułamek dziesiętny skończony to taki, który ma skończoną liczbę cyfr po przecinku. Przykład: 0.25, 1.75, 3.1415.

Ułamek dziesiętny nieskończony okresowy to taki, w którym po pewnym miejscu po przecinku powtarza się pewien ciąg cyfr, zwany okresem. Przykład: 1/3 = 0.3333..., 2/11 = 0.181818... Okres zazwyczaj oznacza się umieszczając kreskę nad powtarzającym się ciągiem cyfr.

Ważne: Każda liczba, która ma nieskończone rozwinięcie dziesiętne nieokresowe, nie jest liczbą wymierną. Takie liczby nazywamy liczbami niewymiernymi (np. √2, π).

Operacje na Liczbach Wymiernych

Na liczbach wymiernych można wykonywać podstawowe operacje arytmetyczne:

Dodawanie: Aby dodać dwa ułamki o różnych mianownikach, należy najpierw sprowadzić je do wspólnego mianownika. Przykład: 1/2 + 1/3 = 3/6 + 2/6 = 5/6.
Odejmowanie: Podobnie jak dodawanie, wymaga sprowadzenia do wspólnego mianownika. Przykład: 2/3 - 1/4 = 8/12 - 3/12 = 5/12.
Mnożenie: Mnożymy licznik przez licznik i mianownik przez mianownik. Przykład: (1/2) * (2/3) = 2/6 = 1/3.
Dzielenie: Dzielenie to mnożenie przez odwrotność. Przykład: (1/2) / (2/3) = (1/2) * (3/2) = 3/4.

Liczby Wymierne a Liczby Całkowite i Naturalne

Warto zauważyć relacje między liczbami wymiernymi a innymi rodzajami liczb:

Liczby Naturalne (ℕ): To liczby całkowite dodatnie i zero (0, 1, 2, 3, ...). Każda liczba naturalna jest liczbą wymierną, ponieważ można ją zapisać jako ułamek z mianownikiem równym 1. (np. 5 = 5/1).
Liczby Całkowite (ℤ): To liczby naturalne oraz ich liczby przeciwne (..., -3, -2, -1, 0, 1, 2, 3, ...). Podobnie jak liczby naturalne, każda liczba całkowita jest liczbą wymierną (np. -7 = -7/1).
Liczby Niewymierne: To liczby, których nie można przedstawić w postaci ułamka p/q, gdzie p i q są liczbami całkowitymi. Przykłady: √2, π, e (liczba Eulera).

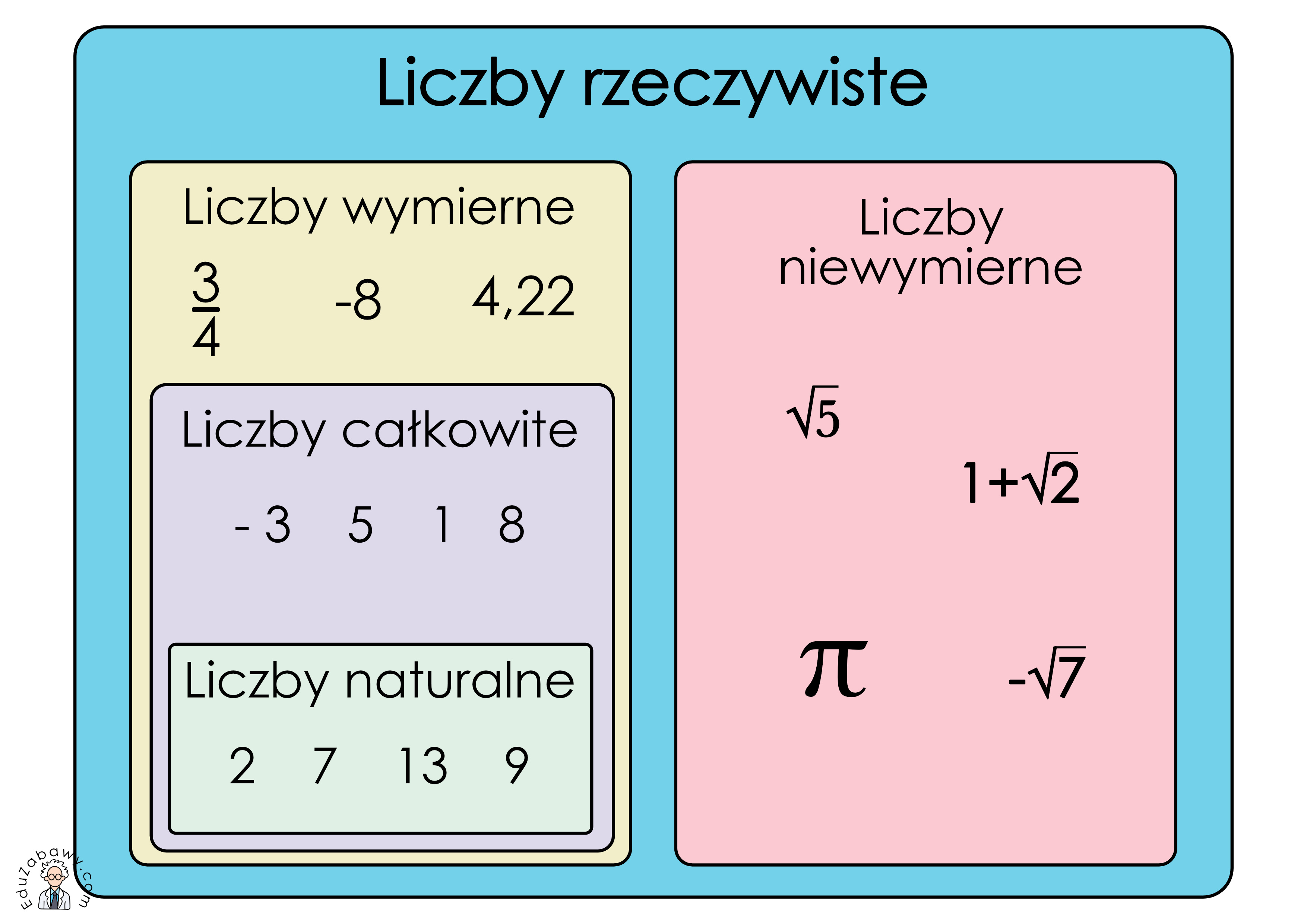
Zatem zbiór liczb wymiernych (ℚ) zawiera w sobie zbiory liczb naturalnych (ℕ) i całkowitych (ℤ): ℕ ⊂ ℤ ⊂ ℚ.

Przykłady Zastosowań Liczb Wymiernych w Życiu Codziennym

Liczby wymierne są wszechobecne w naszym życiu. Oto kilka przykładów:

Gotowanie: Przepisy często podają ilości składników w postaci ułamków (np. 1/2 szklanki mąki, 3/4 łyżeczki soli).
Pomiary: Długość, waga, objętość, czas - wszystkie te wielkości są często wyrażane za pomocą liczb wymiernych. Na przykład, mierząc wzrost, możemy powiedzieć, że ktoś ma 1.75 metra wzrostu.
Finanse: Ceny produktów, oprocentowanie kredytów, podatki - wszystkie te wartości operują na liczbach wymiernych (często wyrażanych w postaci ułamków dziesiętnych). Na przykład, cena produktu może wynosić 9.99 zł.
Sport: Wyniki sportowe, takie jak czas biegu (np. 10.5 sekundy) czy odległość rzutu (np. 85.2 metry), są wyrażane za pomocą liczb wymiernych.
Geometria: W obliczeniach związanych z polem powierzchni, objętością, obwodami figur geometrycznych, często używamy liczb wymiernych.

Przykłady Danych Statystycznych

Liczby wymierne pozwalają nam analizować i interpretować dane statystyczne. Na przykład:

Procenty: Procent to szczególny przypadek ułamka, gdzie mianownik wynosi 100 (np. 25% = 25/100 = 0.25). Procenty używane są do wyrażania proporcji i zmian.
Średnie: Obliczanie średniej polega na sumowaniu wartości i dzieleniu przez liczbę wartości. Wynik jest zazwyczaj liczbą wymierną.
Wskaźniki: Wskaźniki ekonomiczne, takie jak inflacja, PKB, bezrobocie, są często wyrażane za pomocą liczb wymiernych.

Różnica między Liczbami Wymiernymi a Niewymiernymi

Podstawowa różnica polega na tym, czy daną liczbę można wyrazić jako ułamek dwóch liczb całkowitych. Liczby wymierne można, a niewymierne nie można. Liczby niewymierne mają nieskończone i nieokresowe rozwinięcie dziesiętne.

Przykłady:

Wymierne: 3/4 = 0.75, -2/5 = -0.4, 7 = 7.0
Niewymierne: √2 = 1.41421356..., π = 3.14159265...

Zbiór liczb rzeczywistych (ℝ) składa się z liczb wymiernych (ℚ) i niewymiernych. Oznacza to, że każda liczba rzeczywista jest albo wymierna, albo niewymierna.

Podsumowanie

Liczby wymierne to fundamentalne pojęcie matematyczne, mające szerokie zastosowanie w życiu codziennym. Są to liczby, które można wyrazić jako iloraz dwóch liczb całkowitych. Rozumienie liczb wymiernych jest kluczowe dla opanowania bardziej zaawansowanych zagadnień matematycznych. Pamiętaj, że liczby wymierne otaczają nas wszędzie, od gotowania po finanse, i stanowią podstawę wielu obliczeń i pomiarów.

Zachęcamy do dalszego zgłębiania wiedzy na temat liczb wymiernych i ich właściwości. Spróbuj samodzielnie rozwiązywać zadania z wykorzystaniem liczb wymiernych, aby utrwalić zdobytą wiedzę. Matematyka to fascynująca dziedzina, a liczby wymierne stanowią jedynie jej małą, ale niezwykle ważną część.