Co To Jest Figura Symetryczna

W otaczającym nas świecie, pojęcie symetrii odgrywa kluczową rolę, zarówno w matematyce, jak i w sztuce, architekturze oraz naturze. Jednym z podstawowych elementów tej koncepcji jest figura symetryczna. Zrozumienie, co to jest figura symetryczna, pozwala na głębsze docenienie harmonii i porządku, które często umykają naszej uwadze. W tym artykule przyjrzymy się bliżej temu zagadnieniu, analizując różne typy symetrii, ich cechy charakterystyczne oraz przykłady z życia codziennego.

Czym jest Figura Symetryczna?

Figura symetryczna to figura geometryczna, która po wykonaniu pewnej transformacji (np. odbicia, obrotu, przesunięcia) pozostaje niezmieniona. Oznacza to, że po dokonaniu operacji transformacyjnej, figura wygląda dokładnie tak samo, jak przed nią. Najczęściej spotykanymi rodzajami symetrii są symetria osiowa i symetria środkowa, ale istnieją także inne, bardziej złożone formy symetrii.

Symetria Osiowa (Lustrzana)

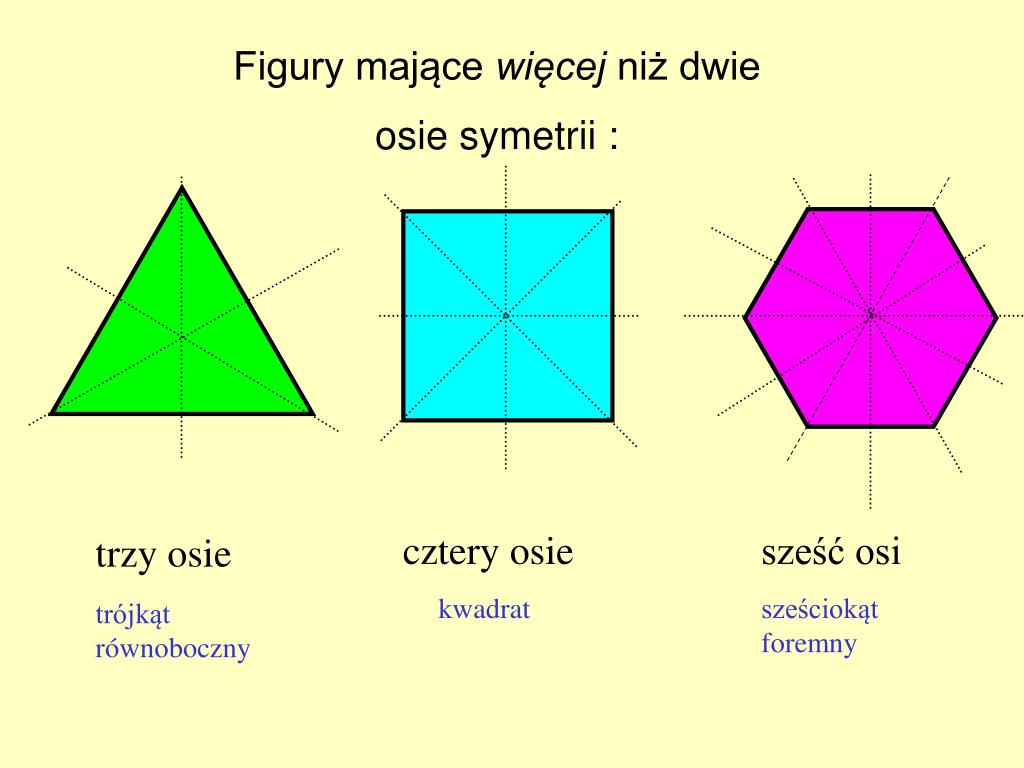
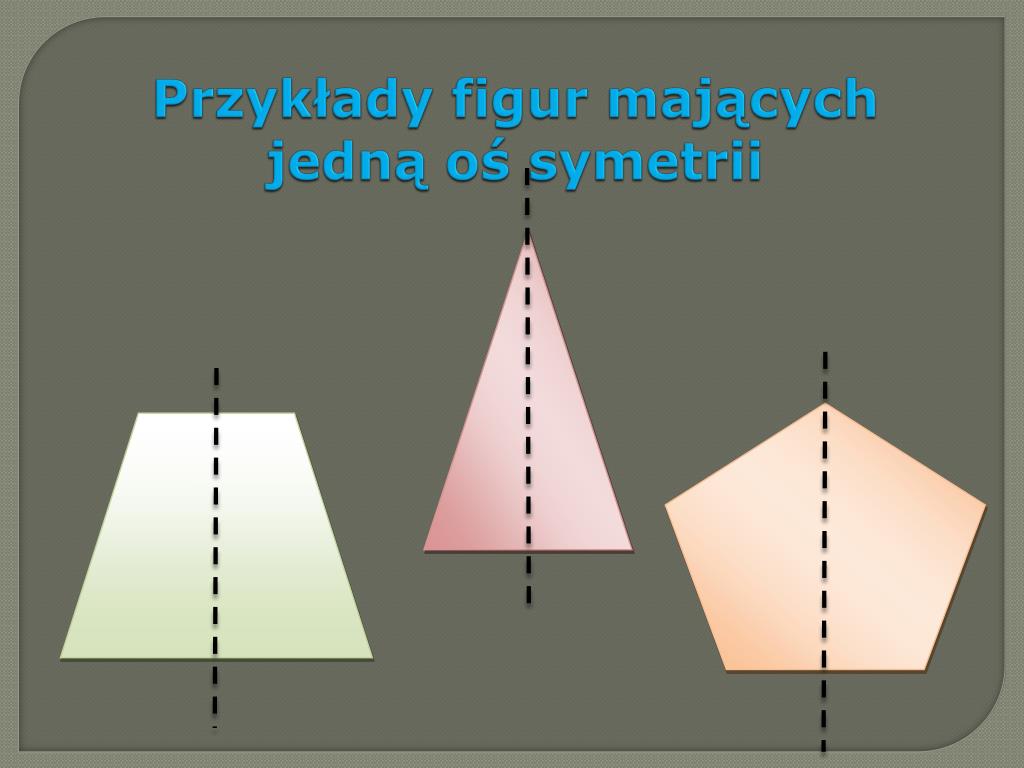
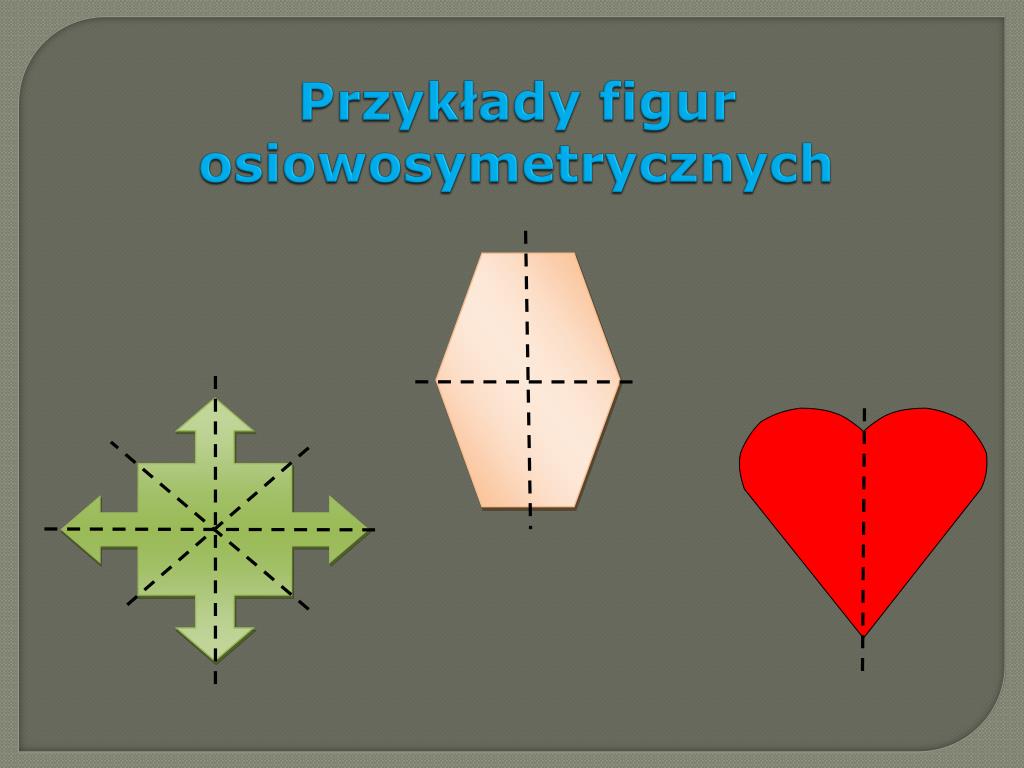
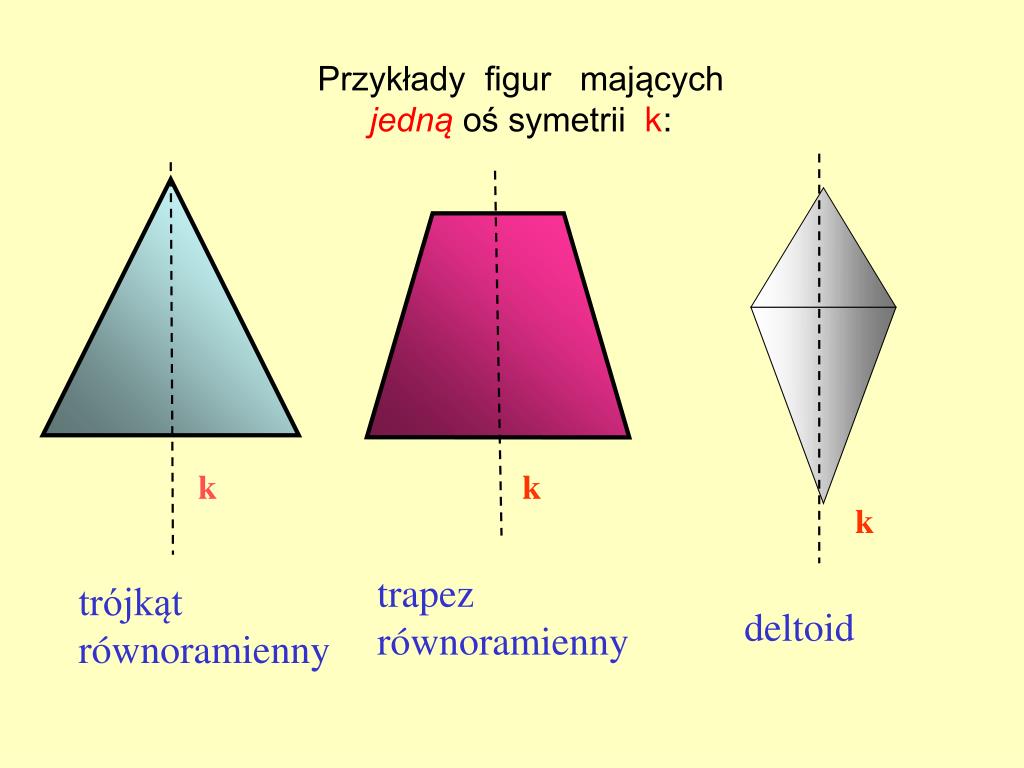
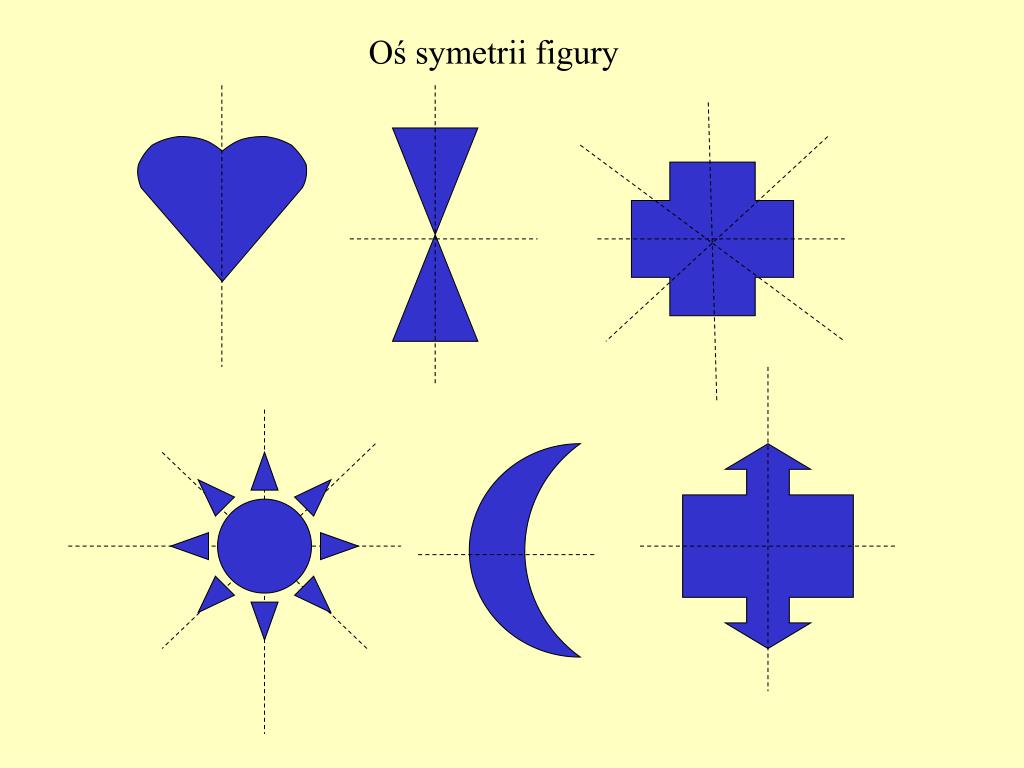
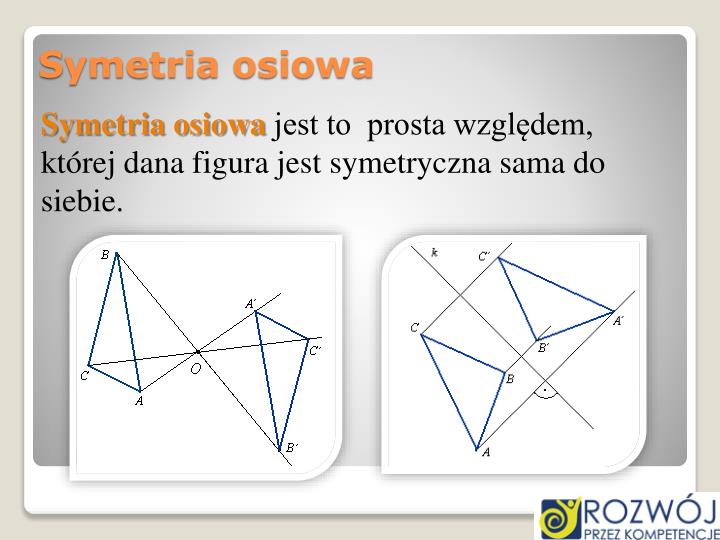
Symetria osiowa, zwana również lustrzaną, występuje wtedy, gdy figura ma jedną lub więcej osi symetrii. Oś symetrii to prosta, która dzieli figurę na dwie identyczne części, będące swoimi lustrzanymi odbiciami. Wyobraźmy sobie, że składamy figurę wzdłuż tej osi – obie połowy idealnie się na siebie nałożą.

Przykłady:

Litera A: Ma jedną oś symetrii pionową.
Motyl: Charakteryzuje się symetrią osiową względem linii przechodzącej przez jego środek.
Kwadrat: Posiada cztery osie symetrii – dwie biegnące przez środki przeciwległych boków i dwie biegnące po przekątnych.

Bardzo ważne jest, aby zrozumieć, że oś symetrii musi dzielić figurę na dokładnie dwie identyczne połowy. Jeżeli po odbiciu względem osi, figura nie wygląda tak samo, to nie jest ona symetryczna osiowo względem tej osi.

Symetria Środkowa (Obrótowa)

Symetria środkowa, znana także jako obrotowa, występuje, gdy figura posiada środek symetrii. Środek symetrii to punkt, względem którego obrócenie figury o 180 stopni daje identyczny obraz. Innymi słowy, jeśli poprowadzimy linię prostą przez środek symetrii i połączymy dowolny punkt figury z tym środkiem, a następnie przedłużymy tę linię o taką samą długość po drugiej stronie, to znajdziemy inny punkt należący do figury.

Przykłady:

Litera S: Ma środek symetrii, ale nie posiada osi symetrii.
Okrąg: Ma środek symetrii w swoim środku i nieskończenie wiele osi symetrii.
Równoległobok: Posiada środek symetrii w punkcie przecięcia przekątnych.

Należy pamiętać, że figura może mieć zarówno symetrię osiową, jak i środkową (np. okrąg), albo tylko jeden z tych rodzajów symetrii (np. litera A ma tylko symetrię osiową, a litera S tylko środkową). Niektóre figury mogą nie posiadać żadnej z tych symetrii.

Inne Rodzaje Symetrii

Oprócz symetrii osiowej i środkowej, istnieją również inne, bardziej zaawansowane rodzaje symetrii, takie jak symetria translacyjna (przesunięcie), symetria obrotowa (obrót o kąt inny niż 180 stopni) i symetria spiralna. Te typy symetrii są częściej spotykane w bardziej złożonych wzorach i strukturach, takich jak kryształy, fraktale czy układy fizyczne.

Symetria translacyjna występuje, gdy przesunięcie figury o pewien wektor daje identyczny obraz (np. wzór na tapecie). Symetria obrotowa charakteryzuje się tym, że obrót figury o określony kąt (mniejszy niż 360 stopni) daje identyczny obraz (np. płatek śniegu). Symetria spiralna jest bardziej skomplikowana i występuje, gdy figura podlega jednocześnie obrotowi i przesunięciu wzdłuż osi obrotu (np. muszla ślimaka).

Symetria w Życiu Codziennym

Symetria jest wszechobecna w naszym otoczeniu. Możemy ją dostrzec w naturze, w budynkach, w przedmiotach codziennego użytku, a nawet w ludzkim ciele. Zrozumienie symetrii pozwala nam docenić piękno i harmonię otaczającego nas świata.

Przykłady:

Architektura: Wiele budynków, takich jak katedry, pałace i mosty, charakteryzuje się symetrią osiową, co nadaje im poczucie stabilności i harmonii. Na przykład, fasada Tadż Mahal w Indiach jest idealnym przykładem symetrii osiowej.
Natura: Wiele roślin i zwierząt wykazuje symetrię osiową lub promienistą. Na przykład, motyle, pszczoły, kwiaty i liście często mają symetryczny kształt. Również ludzkie ciało, choć nie jest idealnie symetryczne, wykazuje ogólną symetrię osiową.
Sztuka: Artyści często wykorzystują symetrię w swoich dziełach, aby stworzyć poczucie równowagi i harmonii. Mozaiki, dywany, witraże i grafiki często bazują na symetrycznych wzorach.
Przedmioty codziennego użytku: Wiele przedmiotów, z których korzystamy na co dzień, ma symetryczny kształt, na przykład talerze, szklanki, samochody i meble. Symetria często ułatwia ich użytkowanie i poprawia ich wygląd estetyczny.

W matematyce, symetria odgrywa kluczową rolę w wielu dziedzinach, takich jak geometria, algebra i analiza. Grupy symetrii są używane do klasyfikacji i analizy struktur matematycznych. Na przykład, kryształy są klasyfikowane na podstawie ich grup symetrii. W fizyce, symetria jest związana z zasadami zachowania. Na przykład, symetria translacyjna prowadzi do zasady zachowania pędu, a symetria obrotowa prowadzi do zasady zachowania momentu pędu.

Dlaczego Symetria jest Ważna?

Symetria jest ważna z wielu powodów. Po pierwsze, jest estetycznie przyjemna. Ludzie generalnie preferują obiekty i wzory, które są symetryczne, ponieważ wydają się bardziej harmonijne i uporządkowane. Po drugie, symetria często ułatwia rozpoznawanie i zapamiętywanie obiektów. Po trzecie, symetria może mieć praktyczne zastosowania. Na przykład, konstrukcje symetryczne są często bardziej stabilne i wytrzymałe.

Ewolucyjnie, preferencja do symetrii może wynikać z faktu, że symetria jest często wskaźnikiem zdrowia i dobrego stanu genetycznego. Zwierzęta, które są bardziej symetryczne, są często postrzegane jako bardziej atrakcyjne i mają większe szanse na znalezienie partnera.

Zauważmy, że brak symetrii, czyli asymetria, również może być ważna i interesująca. Asymetria może dodawać charakteru i oryginalności. W sztuce, asymetria jest często używana do tworzenia napięcia i dynamiki.

Podsumowanie

Figura symetryczna to figura geometryczna, która po wykonaniu pewnej transformacji (np. odbicia, obrotu) pozostaje niezmieniona. Najczęściej spotykanymi rodzajami symetrii są symetria osiowa i symetria środkowa. Symetria jest wszechobecna w naszym otoczeniu i odgrywa ważną rolę w naturze, architekturze, sztuce i matematyce. Zrozumienie symetrii pozwala nam docenić piękno i harmonię otaczającego nas świata.

Zachęcamy do poszukiwania symetrii w swoim otoczeniu. Spróbuj zidentyfikować osie i środki symetrii w różnych obiektach i wzorach. Zwróć uwagę na symetrię w architekturze, w naturze i w sztuce. Zastanów się, dlaczego symetria jest dla nas tak atrakcyjna i jakie ma praktyczne zastosowania. Odkrywanie symetrii może być fascynującą i pouczającą przygodą.