Co To Jest Dwusieczna Kąta

Czy kiedykolwiek zastanawiałeś się, jak idealnie podzielić kąt na dwie równe części? Brzmi jak zadanie wymagające skomplikowanych obliczeń, prawda? A co, gdyby istniała prosta, elegancka linia, która potrafi to zrobić za każdym razem? Ta linia to właśnie dwusieczna kąta. Ten artykuł ma na celu demistyfikację dwusiecznej, wyjaśnienie jej znaczenia i pokazanie, jak ją praktycznie wykorzystać. Niezależnie od tego, czy jesteś uczniem zmagającym się z geometrią, studentem szukającym przypomnienia, czy po prostu osobą ciekawą świata matematyki, ten przewodnik jest dla Ciebie.

Czym jest dwusieczna kąta?

Najprościej mówiąc, dwusieczna kąta to półprosta, która dzieli kąt na dwie równe części. Wyobraź sobie kawałek pizzy. Jeśli przekroisz go idealnie na pół, linia cięcia reprezentuje dwusieczną kąta, który tworzyły brzegi wyciętego kawałka.

To, co odróżnia dwusieczną od zwykłej prostej przecinającej kąt, to właśnie dokładny podział na równe części. Każdy punkt leżący na dwusiecznej jest równo oddalony od ramion kąta. To kluczowa właściwość, która ma ogromne znaczenie w geometrii i nie tylko.

Definicja formalna

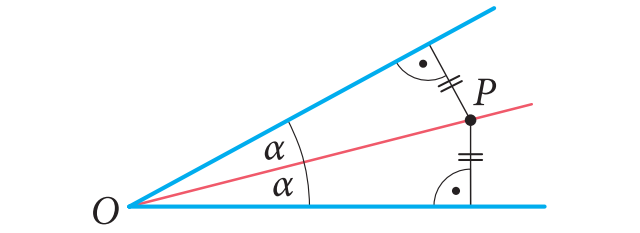
Aby być bardziej precyzyjnym, matematyczna definicja dwusiecznej kąta brzmi: Jest to zbiór wszystkich punktów wewnątrz kąta, które są w równej odległości od ramion kąta. Odległość punktu od prostej mierzy się jako długość odcinka prostopadłego łączącego ten punkt z prostą.

Jak narysować dwusieczną kąta?

Istnieje kilka sposobów na narysowanie dwusiecznej kąta, zarówno z użyciem tradycyjnych narzędzi geometrycznych, jak i nowoczesnych programów. Przyjrzyjmy się najpopularniejszym metodom:

Metoda z użyciem cyrkla i linijki

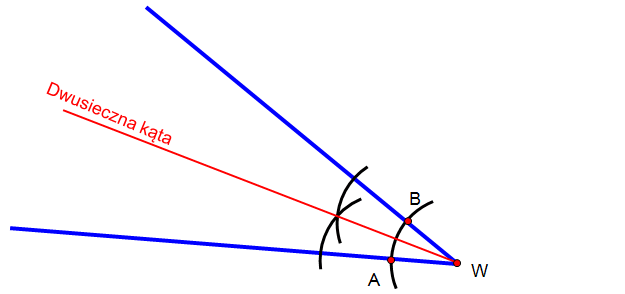
To klasyczna i dokładna metoda, wymagająca jedynie cyrkla i linijki:

1. Krok 1: Umieść ostrze cyrkla w wierzchołku kąta.
2. Krok 2: Narysuj łuk, który przetnie oba ramiona kąta. Nie zmieniaj rozwarcia cyrkla.
3. Krok 3: Umieść ostrze cyrkla w punkcie przecięcia łuku z jednym ramieniem kąta i narysuj kolejny łuk wewnątrz kąta.
4. Krok 4: Powtórz krok 3, umieszczając ostrze cyrkla w punkcie przecięcia łuku z drugim ramieniem kąta.
5. Krok 5: Punkty przecięcia dwóch nowych łuków wyznaczają punkt, przez który przechodzi dwusieczna. Połącz ten punkt z wierzchołkiem kąta za pomocą linijki.

Gratulacje! Właśnie narysowałeś dwusieczną kąta.

Użycie kątomierza

Ta metoda jest szybsza, ale potencjalnie mniej dokładna, szczególnie jeśli używasz kątomierza o niskiej precyzji:

1. Krok 1: Zmierz miarę kąta za pomocą kątomierza.
2. Krok 2: Podziel miarę kąta przez 2.
3. Krok 3: Zaznacz na kątomierzu połowę miary kąta.
4. Krok 4: Połącz wierzchołek kąta z zaznaczonym punktem za pomocą linijki.

Wykorzystanie oprogramowania geometrycznego

Programy takie jak GeoGebra oferują narzędzia do automatycznego tworzenia dwusiecznych. Wystarczy zdefiniować kąt, a program sam narysuje dwusieczną z dużą precyzją.

Właściwości dwusiecznej kąta

Dwusieczna kąta posiada kilka kluczowych właściwości, które czynią ją tak użyteczną w geometrii:

• Podział kąta: Dzieli kąt na dwie równe części. To jej podstawowa i definiująca cecha.
• Punkty równoodległe: Każdy punkt na dwusiecznej jest równoodległy od ramion kąta.
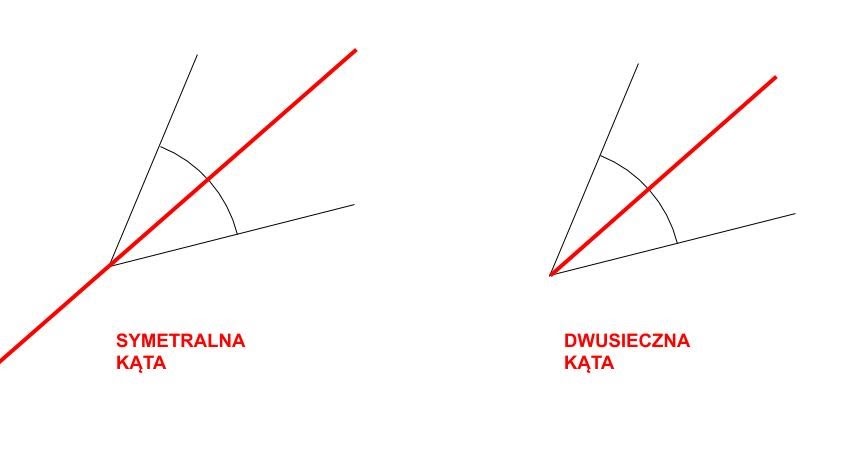
• Oś symetrii: Dwusieczna jest osią symetrii kąta. Oznacza to, że jeśli złożymy kąt wzdłuż dwusiecznej, jego ramiona idealnie się pokryją.
• Związek z okręgami: W trójkącie, punkt przecięcia dwusiecznych kątów wewnętrznych jest środkiem okręgu wpisanego w trójkąt.

Praktyczne zastosowania dwusiecznej kąta

Dwusieczna kąta to nie tylko abstrakcyjna koncepcja matematyczna. Ma wiele praktycznych zastosowań w różnych dziedzinach:

• Architektura i budownictwo: Pomaga w precyzyjnym projektowaniu i budowie konstrukcji, szczególnie przy łączeniu elementów pod kątem.
• Projektowanie graficzne: Wykorzystywana do tworzenia symetrycznych wzorów i ilustracji.
• Nawigacja: W przeszłości używana w nawigacji morskiej do wyznaczania kursów i odległości.
• Robotyka: Stosowana w algorytmach sterowania robotami do precyzyjnego poruszania się i interakcji z otoczeniem.
• Informatyka: Wykorzystywana w algorytmach grafiki komputerowej i przetwarzania obrazów.

Przykład: Wyobraź sobie, że projektujesz ogród i chcesz umieścić fontannę w punkcie równoodległym od dwóch rabat kwiatowych, które tworzą kąt. Dwusieczna kąta pomiędzy rabatami wskaże Ci idealną lokalizację.

Dlaczego dwusieczna kąta jest ważna?

Znajomość dwusiecznej kąta i jej właściwości jest fundamentalna dla zrozumienia wielu zagadnień w geometrii i matematyce. Pozwala na rozwiązywanie problemów związanych z kątami, symetrią, odległościami i konstrukcjami geometrycznymi.

Dodatkowo, zrozumienie dwusiecznej rozwija umiejętność logicznego myślenia i rozwiązywania problemów, które są przydatne nie tylko w matematyce, ale także w wielu innych dziedzinach życia.

Podsumowując, dwusieczna kąta to prosta, ale potężna linia, która dzieli kąt na dwie równe części. Jej właściwości i zastosowania sprawiają, że jest ona niezastąpionym narzędziem w geometrii, architekturze, projektowaniu i wielu innych dziedzinach. Niezależnie od tego, czy jesteś uczniem, studentem, czy profesjonalistą, warto poświęcić czas na zrozumienie tego fundamentalnego pojęcia matematycznego.

Pamiętaj, że matematyka jest jak budowanie z klocków. Im lepiej zrozumiesz podstawowe elementy, tym bardziej skomplikowane i imponujące konstrukcje będziesz w stanie tworzyć. Dwusieczna kąta to jeden z tych klocków, który z pewnością przyda Ci się w przyszłości.

Spróbuj narysować kilka dwusiecznych samodzielnie, używając różnych metod. Zobacz, jak działają w praktyce i jakie możliwości oferują. Z czasem zauważysz, że dwusieczna kąta to nie tylko linia, ale klucz do zrozumienia wielu zagadnień geometrycznych.