Co Jeśli Delta Jest Ujemna

Czy kiedykolwiek rozwiązywałeś równanie kwadratowe i utknąłeś, ponieważ delta wyszła ujemna? Nie martw się, nie jesteś sam! Wiele osób zastanawia się, co to właściwie oznacza i jak sobie z tym poradzić. Ten artykuł jest skierowany do uczniów szkół średnich, studentów, a także wszystkich, którzy chcą lepiej zrozumieć matematykę i równania kwadratowe. Postaramy się wszystko wytłumaczyć w prosty i przystępny sposób.

Co to jest Delta i dlaczego jest ważna?

Delta, oznaczana symbolem Δ, jest kluczowym elementem w równaniu kwadratowym. Pozwala nam szybko określić, ile rozwiązań (pierwiastków) ma dane równanie. Równanie kwadratowe ma postać ax² + bx + c = 0, gdzie a, b, i c to współczynniki liczbowe, a x to nasza niewiadoma. Wzór na deltę to: Δ = b² - 4ac.

Delta jest ważna, ponieważ decyduje o naturze pierwiastków równania kwadratowego:

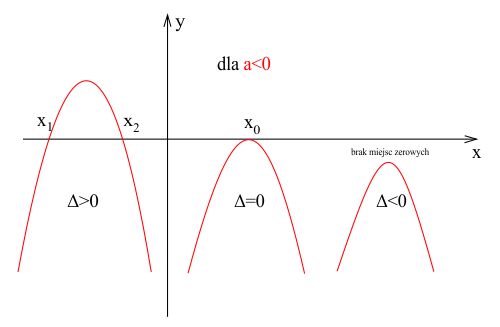
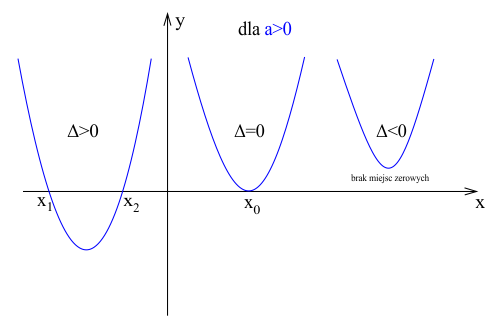
Jeśli Δ > 0, równanie ma dwa różne pierwiastki rzeczywiste.
Jeśli Δ = 0, równanie ma jeden pierwiastek rzeczywisty (często mówimy o dwóch identycznych pierwiastkach).
Jeśli Δ < 0, równanie nie ma pierwiastków rzeczywistych. I właśnie na tym przypadku się dzisiaj skupimy.

Ujemna Delta: Co to oznacza?

Kiedy obliczymy deltę i okaże się, że jej wartość jest ujemna, to oznacza, że równanie kwadratowe nie ma rozwiązań w zbiorze liczb rzeczywistych. Innymi słowy, nie istnieje żadna liczba rzeczywista, którą możemy wstawić za x do równania, aby otrzymać zero. To może być frustrujące, zwłaszcza gdy spodziewaliśmy się znaleźć konkretne rozwiązanie. Ale nie oznacza to, że problem jest nierozwiązywalny!

Dlaczego tak się dzieje? Spójrzmy na wzór na pierwiastki równania kwadratowego:

x_1,2 = (-b ± √Δ) / 2a

Widzimy, że w tym wzorze występuje pierwiastek kwadratowy z delty. Wiemy, że pierwiastek kwadratowy z liczby ujemnej nie jest liczbą rzeczywistą. Dlatego, gdy delta jest ujemna, nie możemy obliczyć pierwiastków w zbiorze liczb rzeczywistych.

Przykład ujemnej delty:

Rozważmy równanie: x² + 2x + 5 = 0.

Obliczamy deltę: Δ = b² - 4ac = 2² - 4 * 1 * 5 = 4 - 20 = -16.

Delta jest ujemna! To oznacza, że to równanie nie ma rozwiązań rzeczywistych.

Co możemy zrobić z ujemną Deltą?

Skoro nie możemy znaleźć rozwiązań rzeczywistych, czy to koniec? Absolutnie nie! Istnieją liczby zespolone, które pozwalają nam znaleźć rozwiązania, nawet gdy delta jest ujemna.

Wprowadzenie do liczb zespolonych:

Liczby zespolone to rozszerzenie zbioru liczb rzeczywistych. Podstawową jednostką urojoną jest i, zdefiniowana jako √(-1). Każda liczba zespolona ma postać a + bi, gdzie a i b są liczbami rzeczywistymi, a i to jednostka urojona. a nazywamy częścią rzeczywistą liczby zespolonej, a b - częścią urojoną.

Używając liczb zespolonych, możemy obliczyć pierwiastek kwadratowy z liczby ujemnej. Na przykład, √(-16) = √(16 * -1) = √16 * √(-1) = 4i.

Rozwiązywanie równania z ujemną deltą przy użyciu liczb zespolonych:

Wróćmy do naszego przykładu: x² + 2x + 5 = 0, gdzie Δ = -16.

Używamy wzoru na pierwiastki:

x_1,2 = (-b ± √Δ) / 2a = (-2 ± √(-16)) / 2 * 1 = (-2 ± 4i) / 2.

Upraszczamy:

x₁ = (-2 + 4i) / 2 = -1 + 2i

x₂ = (-2 - 4i) / 2 = -1 - 2i

Zatem, rozwiązaniami tego równania są liczby zespolone: x₁ = -1 + 2i oraz x₂ = -1 - 2i.

Dlaczego Liczby Zespolone są przydatne?

Możesz się zastanawiać, po co nam te liczby zespolone, skoro nie są liczbami "rzeczywistymi"? Okazuje się, że mają one ogromne zastosowanie w wielu dziedzinach nauki i techniki, takich jak:

Elektrotechnika: Analiza obwodów prądu zmiennego (AC).
Fizyka: Mechanika kwantowa, teoria fal.
Matematyka: Analiza zespolona, teoria liczb.
Informatyka: Przetwarzanie sygnałów, grafika komputerowa.

Bez liczb zespolonych wiele technologii, z których korzystamy na co dzień, nie byłoby możliwe.

Jak unikać błędów przy obliczaniu delty?

Obliczanie delty wydaje się proste, ale łatwo o błędy. Oto kilka wskazówek, jak ich unikać:

Upewnij się, że równanie jest w postaci ogólnej: ax² + bx + c = 0. Często trzeba najpierw przekształcić równanie, aby doprowadzić je do tej postaci.
Uważaj na znaki: Szczególną uwagę zwróć na znaki plus i minus, zwłaszcza przy obliczaniu b² i -4ac.
Sprawdź swoje obliczenia: Po obliczeniu delty, warto jeszcze raz sprawdzić, czy nie popełniłeś błędu.
Użyj kalkulatora: Jeśli masz trudności z obliczeniami, użyj kalkulatora, aby uniknąć błędów. Pamiętaj, aby wprowadzać dane ostrożnie.

Podsumowanie:

Ujemna delta w równaniu kwadratowym oznacza, że równanie nie ma rozwiązań rzeczywistych. Nie oznacza to jednak, że problem jest nierozwiązywalny! Możemy użyć liczb zespolonych, aby znaleźć rozwiązania. Liczby zespolone są niezwykle przydatne w wielu dziedzinach nauki i techniki, dlatego warto je znać i rozumieć. Pamiętaj o uważnym obliczaniu delty i unikaniu błędów. Zrozumienie delty i liczb zespolonych otwiera przed Tobą nowe możliwości w matematyce i naukach ścisłych. Nie bój się trudnych zadań i eksploruj świat matematyki!

Mam nadzieję, że ten artykuł pomógł Ci lepiej zrozumieć, co zrobić, gdy delta jest ujemna. Pamiętaj, że matematyka to ciągłe uczenie się i odkrywanie, więc nie zrażaj się trudnościami i dąż do celu!