Boki W Trójkącie 30 60 90

W geometrii, trójkąt o kątach 30°, 60° i 90° zajmuje szczególne miejsce. Jego unikalne właściwości sprawiają, że jest nie tylko interesującym obiektem do nauki, ale także praktycznym narzędziem w wielu dziedzinach, od budownictwa po trygonometrię. W tym artykule zgłębimy tajniki tego trójkąta, analizując jego charakterystyczne cechy, zależności między bokami oraz praktyczne zastosowania.
Charakterystyka trójkąta 30-60-90
Kąty
Trójkąt 30-60-90, jak sama nazwa wskazuje, charakteryzuje się obecnością kątów o miarach 30 stopni, 60 stopni i 90 stopni. Kąt prosty (90 stopni) czyni go trójkątem prostokątnym, co otwiera drzwi do wykorzystania twierdzenia Pitagorasa i innych właściwości trójkątów prostokątnych.
Suma kątów w każdym trójkącie, w tym w trójkącie 30-60-90, zawsze wynosi 180 stopni. Wiedząc o dwóch kątach, zawsze możemy obliczyć trzeci.
Zależności między bokami
Najważniejszą cechą trójkąta 30-60-90 są charakterystyczne proporcje między długościami jego boków. Relacje te są stałe i pozwalają na łatwe obliczanie długości nieznanych boków, znając tylko jeden z nich.
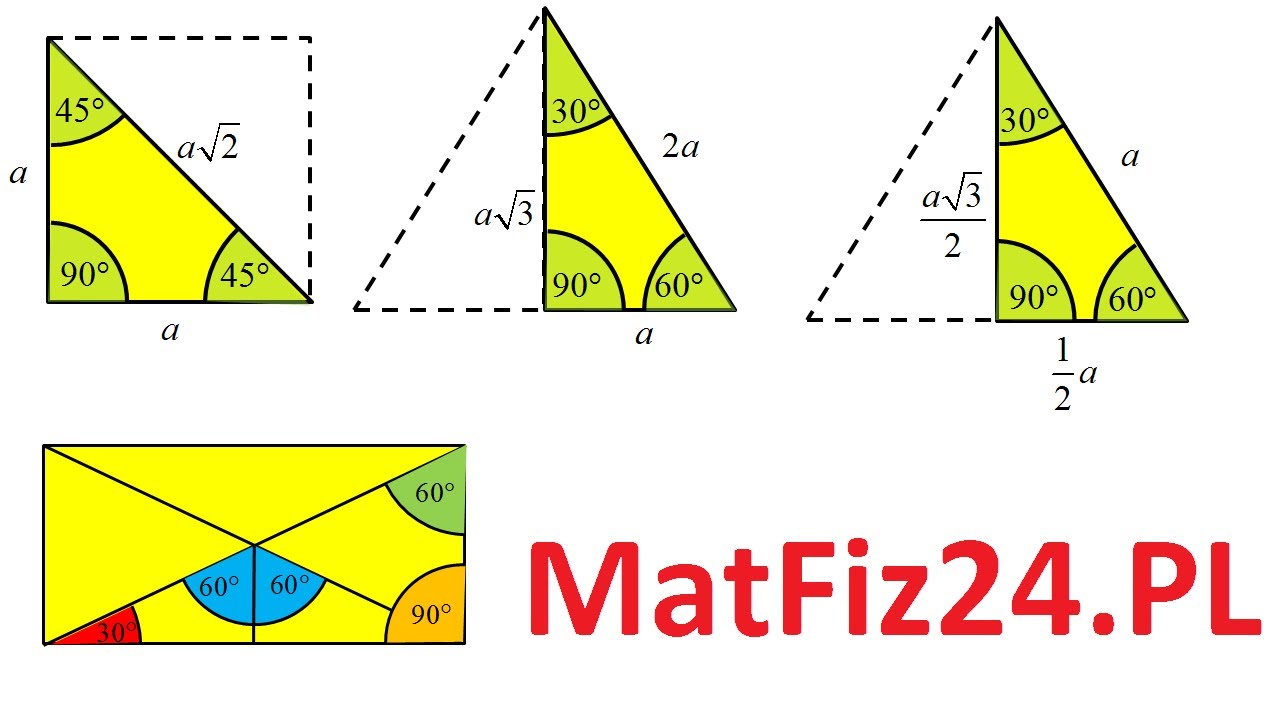
Jeśli przyjmiemy, że najkrótszy bok (leżący naprzeciw kąta 30°) ma długość a, to:
- Przeciwprostokątna (bok leżący naprzeciw kąta prostego) ma długość 2a.
- Drugi bok (leżący naprzeciw kąta 60°) ma długość a√3.
Inaczej mówiąc: stosunek boków w trójkącie 30-60-90 wynosi 1 : √3 : 2.
Dowód zależności między bokami
Skąd się biorą te zależności? Najłatwiej to zrozumieć, rozważając trójkąt równoboczny o boku 2a. Jeśli narysujemy wysokość w takim trójkącie, podzieli ona go na dwa identyczne trójkąty prostokątne 30-60-90.
Wysokość trójkąta równobocznego dzieli bok, na który opada, na dwie równe części. Zatem najkrótszy bok naszego trójkąta 30-60-90 ma długość a (połowa boku trójkąta równobocznego). Przeciwprostokątna to jednocześnie bok trójkąta równobocznego, czyli 2a. Długość drugiego boku (wysokości trójkąta równobocznego) można obliczyć z twierdzenia Pitagorasa: (2a)² = a² + h², co daje h = a√3.
Wykorzystanie trójkąta 30-60-90
Trygonometria
Trójkąt 30-60-90 jest fundamentem trygonometrii. Znając jego boki, możemy łatwo obliczyć wartości funkcji trygonometrycznych dla kątów 30 i 60 stopni.
Na przykład:
- sin(30°) = a / 2a = 1/2
- cos(30°) = a√3 / 2a = √3/2
- tan(30°) = a / a√3 = 1/√3 = √3/3
- sin(60°) = a√3 / 2a = √3/2
- cos(60°) = a / 2a = 1/2
- tan(60°) = a√3 / a = √3
Te wartości są powszechnie używane w fizyce, inżynierii i innych naukach ścisłych.
Budownictwo i architektura
Trójkąt 30-60-90 znajduje zastosowanie w budownictwie, np. przy projektowaniu dachów, schodów, czy ramp. Znając kąty i proporcje, można precyzyjnie obliczyć wymiary poszczególnych elementów konstrukcyjnych.
Przykład: Dach o kącie nachylenia 30 stopni względem poziomu tworzy z pionową ścianą trójkąt 30-60-90. Znając wysokość ściany (krótszy bok trójkąta), możemy obliczyć długość połaci dachu (przeciwprostokątna) i odległość od ściany do krawędzi dachu (drugi bok trójkąta).
Inżynieria
W inżynierii mechanicznej, trójkąt 30-60-90 może być wykorzystywany do analizy sił działających na obiekty pod kątem. Rozkład sił na składowe często prowadzi do powstania trójkątów prostokątnych, w tym trójkątów 30-60-90, co ułatwia obliczenia.
Przykład: Analiza sił działających na zbocze nachylone pod kątem 30 stopni. Siła grawitacji działająca na obiekt na zboczu może być rozłożona na dwie składowe: równoległą do zbocza i prostopadłą do zbocza. Składowe te tworzą trójkąt prostokątny z siłą grawitacji jako przeciwprostokątną. Jeśli kąt nachylenia zbocza wynosi 30 stopni, otrzymujemy trójkąt 30-60-90, co ułatwia obliczenie wartości składowych siły.
Nawigacja i geodezja
W nawigacji i geodezji, trójkąty 30-60-90 mogą być używane do obliczania odległości i wysokości, szczególnie w połączeniu z innymi technikami pomiarowymi.
Przykład: Załóżmy, że stoimy w pewnej odległości od wysokiej budowli i mierzymy kąt pod jakim widzimy jej wierzchołek. Jeśli kąt ten wynosi 60 stopni, a odległość od budowli do miejsca, gdzie stoimy (czyli długość boku przyległego do kąta 60 stopni) jest znana, to możemy obliczyć wysokość budowli (długość boku przeciwległego do kąta 60 stopni) wykorzystując zależność tangensa kąta 60 stopni.
Przykłady liczbowe
Aby utrwalić wiedzę, przeanalizujmy kilka przykładów obliczeniowych:
Przykład 1: W trójkącie 30-60-90 najkrótszy bok ma długość 5 cm. Oblicz długość pozostałych boków.
Rozwiązanie: * Przeciwprostokątna: 2 * 5 cm = 10 cm * Drugi bok: 5 cm * √3 ≈ 8.66 cm
Przykład 2: W trójkącie 30-60-90 przeciwprostokątna ma długość 12 cm. Oblicz długość pozostałych boków.
Rozwiązanie: * Najkrótszy bok: 12 cm / 2 = 6 cm * Drugi bok: 6 cm * √3 ≈ 10.39 cm
Przykład 3: W trójkącie 30-60-90 bok leżący naprzeciw kąta 60 stopni ma długość 7√3 cm. Oblicz długość pozostałych boków.
Rozwiązanie: * Najkrótszy bok: (7√3 cm) / √3 = 7 cm * Przeciwprostokątna: 2 * 7 cm = 14 cm
Ograniczenia i pułapki
Ważne jest, aby pamiętać, że zależności między bokami trójkąta 30-60-90 działają tylko wtedy, gdy mamy do czynienia z dokładnie takim trójkątem, czyli o kątach 30°, 60° i 90°. Pomylenie go z innym trójkątem prostokątnym prowadzi do błędnych obliczeń.
Dodatkowo, obliczenia z pierwiastkami kwadratowymi mogą czasami być przybliżone, zwłaszcza gdy wymagana jest duża precyzja. W takich przypadkach należy używać kalkulatora lub programów komputerowych.
Podsumowanie
Trójkąt 30-60-90 to potężne narzędzie w geometrii, trygonometrii i wielu dziedzinach nauki i inżynierii. Jego unikalne proporcje pozwalają na szybkie i łatwe obliczanie długości boków i wartości funkcji trygonometrycznych. Zrozumienie jego właściwości jest niezbędne dla każdego, kto zajmuje się matematyką, fizyką, inżynierią, architekturą czy nawigacją.
Zachęcamy do dalszego zgłębiania wiedzy na temat trójkątów i ich zastosowań. Rozwiązywanie zadań i analiza praktycznych przykładów pozwoli na pełne zrozumienie i wykorzystanie potencjału trójkąta 30-60-90. Pamiętaj, że ćwiczenie czyni mistrza!