Boki Trapezu Równoramiennego Mają Długości 24 Cm 15 Cm

Dzień dobry! Widzę, że macie problem z zadaniem dotyczącym trapezu równoramiennego. Spróbuję Wam to wytłumaczyć krok po kroku, żeby było jasne i zrozumiałe. Skupimy się na sytuacji, w której boki trapezu równoramiennego mają długości 24 cm i 15 cm, a my chcemy zrozumieć, co to oznacza i jak rozwiązywać zadania z tym związane.

Rozumienie trapezu równoramiennego

Na początek, przypomnijmy sobie, czym jest trapez równoramienny. To czworokąt, który ma jedną parę boków równoległych (nazywamy je podstawami) oraz dwa boki nierównoległe (ramiona) o równej długości. W naszym przypadku mamy podane długości 24 cm i 15 cm. Ważne jest, żeby zrozumieć, które z tych długości odpowiadają ramionom, a które podstawom.

Zazwyczaj, w tego typu zadaniach, ramiona (czyli te boki nierównoległe) mają podaną jedną długość, bo są równe. Jeżeli mamy podane tylko dwie długości, a wiemy, że to trapez równoramienny, to jedna z tych długości musi dotyczyć ramion.

Teraz pojawia się pytanie: czy 24 cm i 15 cm to długości ramion i jednej z podstaw, czy też długości dwóch podstaw? Kluczem jest zrozumienie, że w trapezie równoramiennym ramiona muszą być równe. Zatem, jeśli mamy podane tylko dwie długości, to sytuacja, w której 24 cm i 15 cm to długości ramion i podstaw, jest niemożliwa, bo ramiona musiałyby mieć różne długości. To wyklucza nam jedną możliwość.

Zatem, długości 24 cm i 15 cm muszą odnosić się do długości dwóch podstaw trapezu.

Załóżmy, że dłuższa podstawa ma długość 24 cm, a krótsza 15 cm. Wtedy ramiona trapezu muszą mieć jakąś inną, nieznaną nam na razie długość. Jeżeli w zadaniu mielibyśmy podaną długość ramienia, to moglibyśmy zająć się dalszymi obliczeniami, na przykład wyznaczaniem wysokości trapezu, jego pola powierzchni, obwodu, czy też analizą kątów.

Przykładowe zadania i sposoby ich rozwiązywania

Żeby lepiej to zrozumieć, rozważmy kilka przykładowych zadań, zakładając, że mamy trapez równoramienny o podstawach długości 24 cm i 15 cm:

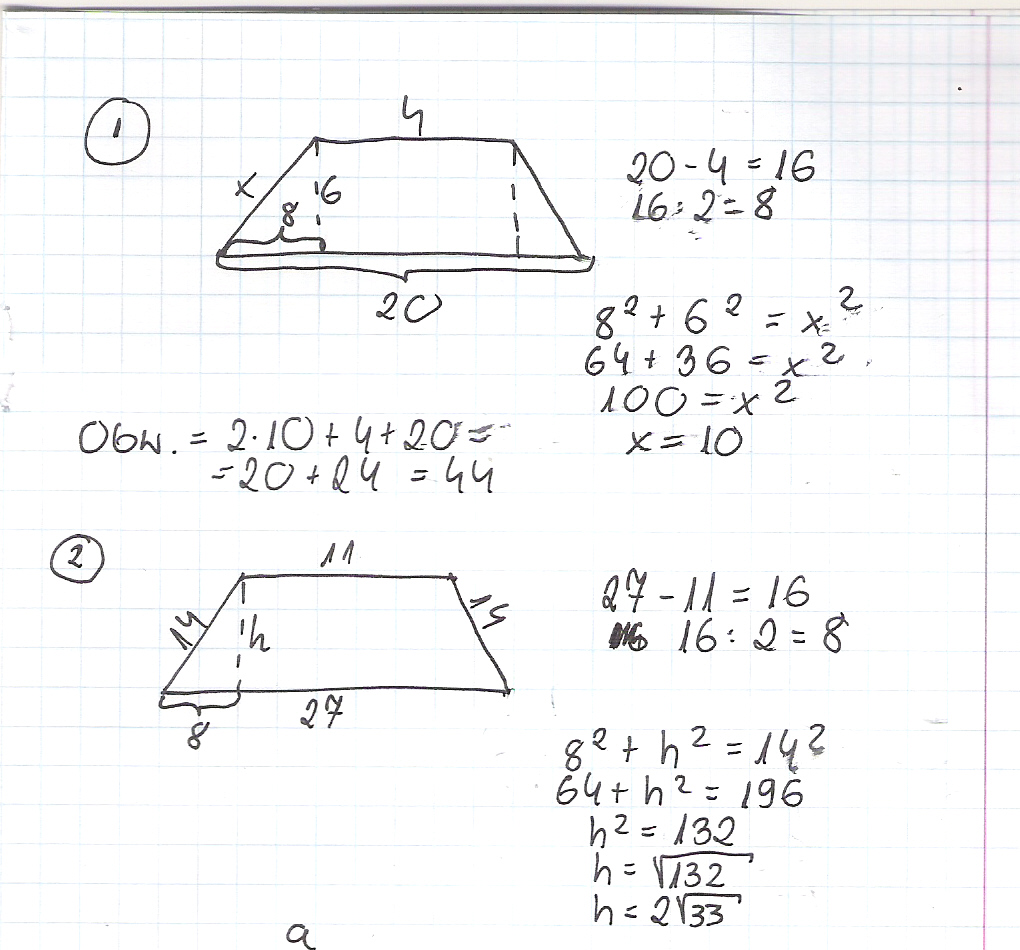
Zadanie 1: Obliczenie długości ramienia, gdy znamy obwód trapezu.

Załóżmy, że obwód trapezu wynosi 73 cm. Obwód to suma długości wszystkich boków. Wiemy, że podstawa dolna ma 24 cm, podstawa górna 15 cm. Oznaczmy długość ramienia jako 'x'. Ponieważ trapez jest równoramienny, oba ramiona mają długość 'x'. Zatem:

24 cm + 15 cm + x + x = 73 cm

39 cm + 2x = 73 cm

2x = 73 cm - 39 cm

2x = 34 cm

x = 17 cm

Wniosek: Długość ramienia trapezu wynosi 17 cm.
Zadanie 2: Obliczenie wysokości trapezu, gdy znamy długość ramienia i pole powierzchni.

Załóżmy, że pole powierzchni trapezu wynosi 195 cm², a długość ramienia wynosi 13 cm. Wzór na pole trapezu to:

Pole = ( (a + b) / 2 ) * h, gdzie 'a' i 'b' to długości podstaw, a 'h' to wysokość.

W naszym przypadku:

195 cm² = ( (24 cm + 15 cm) / 2 ) * h

195 cm² = ( 39 cm / 2 ) * h

195 cm² = 19.5 cm * h

h = 195 cm² / 19.5 cm

h = 10 cm

Wniosek: Wysokość trapezu wynosi 10 cm.

Teraz możemy zweryfikować, czy długość ramienia (13cm) jest możliwa przy wysokości 10cm. Możemy skorzystać z twierdzenia Pitagorasa. Różnica między długością dłuższej podstawy i krótszej to 24-15 = 9 cm. Dzieląc to na połowę otrzymujemy 4.5cm. Teraz korzystamy z twierdzenia Pitagorasa: a^2 + b^2 = c^2, gdzie a to połowa różnicy podstaw (4.5cm), b to wysokość (10cm), a c to ramię (13cm).
1. 5^2 + 10^2 = 20.25 + 100 = 120.25. Pierwiastek z 120.25 to w przybliżeniu 10.97cm. W zadaniu podano, że ramię ma długość 13cm, więc to zadanie jest nieco nierealne. Dla wysokości 10cm, ramię musiałoby mieć długość około 10.97cm.
Zadanie 3: Obliczenie miar kątów przy podstawie.

To zadanie wymaga dodatkowych informacji, np. długości ramienia lub wysokości trapezu. Bez tych danych nie da się jednoznacznie wyznaczyć miar kątów. Jeżeli znalibyśmy wysokość, moglibyśmy obliczyć sinus lub cosinus kąta przy podstawie, a następnie użyć funkcji trygonometrycznych (sinus, cosinus, tangens) do znalezienia miary kąta.

Dodatkowe wskazówki

Rysunek: Zawsze, gdy masz zadanie z geometrii, narysuj sobie trapez. To bardzo pomaga zrozumieć, co jest dane i co trzeba obliczyć. Oznacz na rysunku wszystkie podane długości i kąty.
Wzory: Przypomnij sobie wzory na pole trapezu, obwód trapezu oraz twierdzenie Pitagorasa. Są one bardzo przydatne w rozwiązywaniu zadań.
Zależności: Pamiętaj o zależnościach w trapezie równoramiennym: ramiona są równe, kąty przy każdej z podstaw są równe.

Podsumowanie

Mam nadzieję, że teraz rozumiecie lepiej, jak podchodzić do zadań z trapezem równoramiennym, w których znane są długości podstaw. Pamiętajcie o rysowaniu, korzystaniu ze wzorów i analizowaniu danych. Powodzenia w rozwiązywaniu zadań!