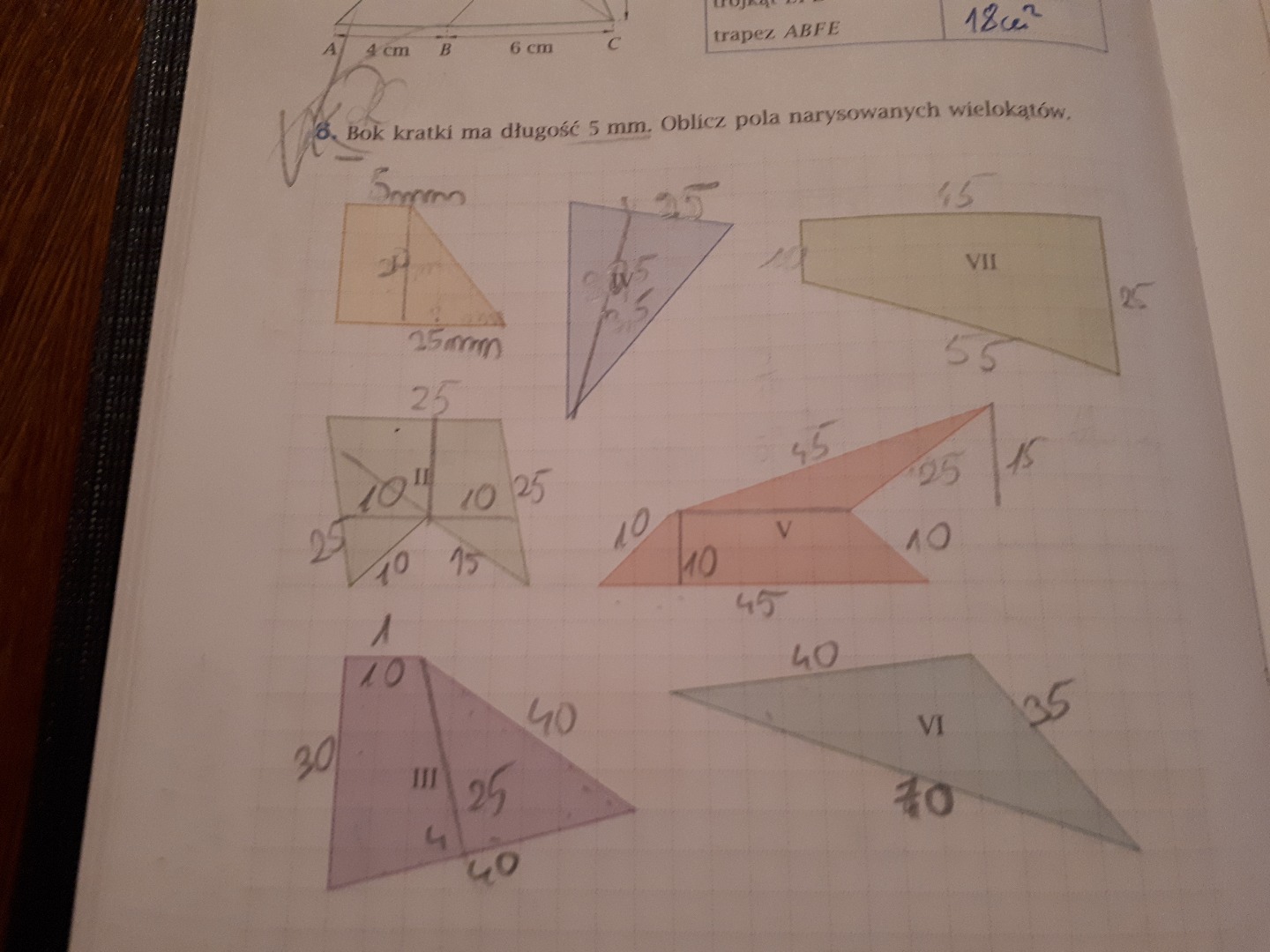
Bok Kratki Ma Długość 5 Mm Oblicz Pola Narysowanych Wielokątów

Dobrze, spróbujmy to wyjaśnić krok po kroku. Załóżmy, że mamy narysowane wielokąty, a bok kratki (czyli pojedynczego kwadracika w zeszycie) ma długość 5 mm. Chcemy obliczyć pola tych wielokątów.

Na początek, co to znaczy "obliczyć pole"? To tak, jakbyśmy chcieli zmierzyć, ile miejsca zajmuje dany kształt na płaskiej powierzchni. Mierzymy to w jednostkach kwadratowych, na przykład w milimetrach kwadratowych (mm²) jeśli bok naszej kratki ma 5 mm.

Krok 1: Policz kratki!

Najprostszy sposób na obliczenie pola, jeśli wielokąt jest narysowany na kratce, to policzenie, ile pełnych kratek zawiera. Jeśli masz kwadrat, który składa się z 4 kratek (2 kratki na długość i 2 na szerokość), to znaczy, że zajmuje 4 jednostki pola "kratkowego".

Krok 2: Co z niepełnymi kratkami?

Często zdarza się, że wielokąt nie zawiera tylko pełnych kratek, ale również kawałki. Co wtedy? Mamy kilka opcji:

• Szacowanie: Możemy oszacować, ile mniej więcej kratek stanowi dany kawałek. Na przykład, jeśli widzimy kawałek, który wygląda mniej więcej jak połowa kratki, to liczymy go jako 0.5. Jeśli wygląda jak trzy czwarte kratki, to liczymy go jako 0.75.
• Łączenie: Możemy próbować łączyć kawałki kratek, żeby stworzyć pełne kratki. Na przykład, jeśli mamy dwa kawałki, które razem tworzą mniej więcej całą kratkę, to możemy je zsumować i policzyć jako 1 kratkę.
• Uśrednianie: Możemy uśredniać, czyli zbierać wszystkie kawałki i próbować oszacować, ile pełnych kratek by z nich wyszło.

Krok 3: Oblicz pole jednej kratki!

Wiemy, że bok kratki ma 5 mm. Pole kwadratu (czyli jednej kratki) obliczamy, mnożąc długość boku przez długość boku. Czyli:

Pole kratki = 5 mm * 5 mm = 25 mm²

Krok 4: Pomnóż liczbę kratek przez pole jednej kratki!

Po policzeniu wszystkich kratek (pełnych i niepełnych) i oszacowaniu ich łącznej liczby, mnożymy tę liczbę przez pole jednej kratki, czyli przez 25 mm². To da nam przybliżone pole całego wielokąta w milimetrach kwadratowych.

Przykład:

Załóżmy, że policzyliśmy, że nasz wielokąt zawiera:

• 10 pełnych kratek
• Kawałki, które razem dają mniej więcej 3.5 kratki

Czyli łącznie mamy 10 + 3.5 = 13.5 kratek.

Teraz mnożymy to przez pole jednej kratki:

Pole wielokąta = 13.5 * 25 mm² = 337.5 mm²

Czyli przybliżone pole naszego wielokąta wynosi 337.5 mm².

Bardziej skomplikowane kształty i wzory

Czasami wielokąty są bardziej skomplikowane i trudno dokładnie policzyć kratki. Wtedy możemy spróbować podzielić je na prostsze kształty, takie jak prostokąty, trójkąty, a nawet trapezy, których pola umiemy obliczyć za pomocą wzorów. Następnie sumujemy pola tych prostszych kształtów.

Prostokąt: Pole prostokąta to długość pomnożona przez szerokość. Jeśli na kratce prostokąt ma 3 kratki długości i 2 kratki szerokości, to jego wymiary to 3 * 5 mm = 15 mm (długość) i 2 * 5 mm = 10 mm (szerokość). Zatem pole to 15 mm * 10 mm = 150 mm².

Trójkąt: Pole trójkąta to połowa iloczynu długości podstawy i wysokości. Podstawa i wysokość muszą być do siebie prostopadłe. Jeśli trójkąt na kratce ma podstawę długości 4 kratki i wysokość długości 3 kratki, to podstawa ma 4 * 5 mm = 20 mm, a wysokość 3 * 5 mm = 15 mm. Zatem pole to (20 mm * 15 mm) / 2 = 150 mm².

Trapez: Pole trapezu to połowa sumy długości podstaw pomnożona przez wysokość. Jeśli trapez na kratce ma podstawy długości 2 i 4 kratki oraz wysokość długości 3 kratki, to podstawy mają 2 * 5 mm = 10 mm i 4 * 5 mm = 20 mm, a wysokość 3 * 5 mm = 15 mm. Zatem pole to ((10 mm + 20 mm) / 2) * 15 mm = (30 mm / 2) * 15 mm = 15 mm * 15 mm = 225 mm².

Przykładowe zadanie:

Załóżmy, że mamy wielokąt, który możemy podzielić na prostokąt o wymiarach 4x2 kratki oraz trójkąt o podstawie 3 kratki i wysokości 2 kratki.

1. Prostokąt:

   • Długość: 4 * 5 mm = 20 mm
   • Szerokość: 2 * 5 mm = 10 mm
   • Pole prostokąta: 20 mm * 10 mm = 200 mm²

2. Trójkąt:

   • Podstawa: 3 * 5 mm = 15 mm
   • Wysokość: 2 * 5 mm = 10 mm
   • Pole trójkąta: (15 mm * 10 mm) / 2 = 75 mm²

3. Pole całkowite:

   • Pole wielokąta: 200 mm² + 75 mm² = 275 mm²

Ważne jest, aby być dokładnym przy liczeniu kratek i pomiarach, aby uzyskać jak najdokładniejszy wynik. Im dokładniej podzielimy skomplikowany kształt na prostsze, tym dokładniejsze będzie obliczenie pola. Pamiętaj też, że wynik jest w milimetrach kwadratowych (mm²), ponieważ taka jest jednostka pola, gdy bok kratki ma długość 5 mm.

Podsumowanie

Obliczanie pola wielokątów na kratce o boku 5 mm sprowadza się do:

1. Policzenia kratek (pełnych i oszacowania niepełnych).
2. Obliczenia pola jednej kratki (25 mm²).
3. Pomnożenia liczby kratek przez pole jednej kratki.

Dla bardziej skomplikowanych kształtów:

1. Podzielenia wielokąta na prostsze figury (prostokąty, trójkąty, trapezy).
2. Obliczenia pól tych figur.
3. Zsumowania pól tych figur.

Pamiętaj o jednostkach! Wynik zawsze będzie w milimetrach kwadratowych (mm²). Ćwicz i staraj się być jak najbardziej dokładnym! Powodzenia!