Balon Opada Ze Stałą Prędkością Jaką Masę Balastu Należy Wyrzucić

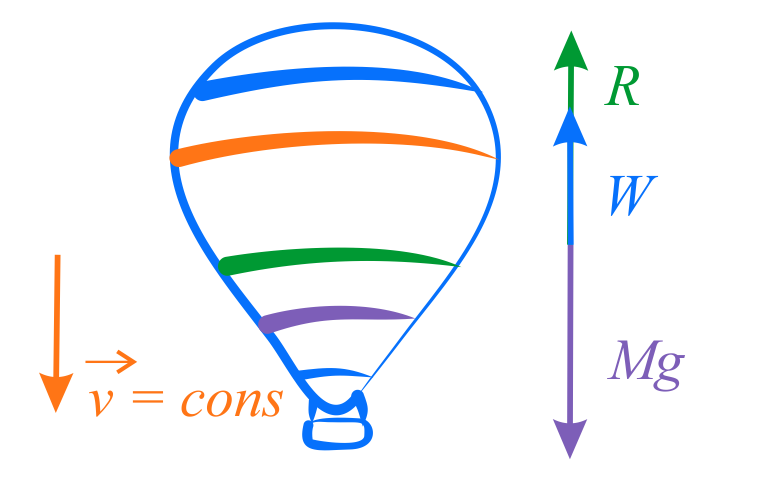
Załóżmy, że mamy balon, który opada ze stałą prędkością. To bardzo ważna informacja, bo od razu wiemy, że siły działające na balon są w równowadze. To oznacza, że siła ciężkości, czyli masa balonu łącznie z balastem pomnożona przez przyspieszenie ziemskie (g), jest równa sile oporu powietrza i sile wyporu.

Sytuacja jest dynamiczna. Balon nie stoi w miejscu, ale opada ze stałą prędkością. Stała prędkość oznacza, że przyspieszenie jest równe zero. Siła wypadkowa działająca na balon również musi być zerowa. Zatem, suma sił skierowanych w dół (ciężar balonu i balastu) równa się sumie sił skierowanych w górę (siła wyporu i opór powietrza).

Zdefiniujmy zmienne. Niech m oznacza masę balonu (bez balastu), M oznacza masę balastu, g to przyspieszenie ziemskie (około 9.81 m/s²). Siła ciężkości działająca na balon z balastem to (m + M)g. Oznaczmy siłę wyporu jako B, a siłę oporu powietrza jako Op.

Zatem, w pierwszym przypadku (balon opada ze stałą prędkością) mamy równanie:

(m + M)g = B + Op

Teraz wyobraźmy sobie, że wyrzucamy pewną masę balastu, którą oznaczamy jako ΔM. Po wyrzuceniu balastu, balon zacznie się wznosić (przynajmniej na moment). Zauważmy, że siła wyporu (B) się nie zmienia, bo nie zmieniamy objętości balonu (zakładamy, że objętość balonu jest stała i nie uwzględniamy wpływu wysokości na siłę wyporu – małe przybliżenie). Siła oporu powietrza (Op) początkowo też się nie zmienia, bo prędkość początkowo pozostaje taka sama. Zatem, po wyrzuceniu balastu, równanie sił wygląda tak:

(m + M - ΔM)g < B + Op

Balon, po wyrzuceniu balastu, zacznie się wznosić z pewnym przyspieszeniem. Ale my chcemy, żeby balon przestał opadać i zaczął się wznosić ze stałą prędkością. To oznacza, że musimy wyrzucić taką ilość balastu (ΔM), żeby znowu zapanowała równowaga sił. Tym razem siła wypadkowa musi być skierowana do góry i równa zero. Oznacza to, że siła wyporu plus siła oporu powietrza (która teraz będzie skierowana w dół, bo balon się wznosi) musi być równa sile ciężkości balonu i pozostałego balastu.

Zatem, w drugim przypadku (balon wznosi się ze stałą prędkością) mamy równanie:

(m + M - ΔM)g = B - Op

Zauważmy, że siła oporu powietrza zmieniła znak, ponieważ kierunek ruchu się zmienił. Teraz naszym celem jest znalezienie ΔM. Mamy dwa równania:

(m + M)g = B + Op
(m + M - ΔM)g = B - Op

Możemy odjąć drugie równanie od pierwszego:

(m + M)g - (m + M - ΔM)g = (B + Op) - (B - Op)

Upraszczając:

ΔMg = 2Op

Stąd:

ΔM = 2Op / g

To oznacza, że masa balastu, którą musimy wyrzucić, jest równa podwojonej sile oporu powietrza podzielonej przez przyspieszenie ziemskie. Ale zaraz, skąd mamy wziąć wartość siły oporu powietrza?

Musimy wrócić do pierwszego równania:

(m + M)g = B + Op

Stąd:

Op = (m + M)g - B

Podstawiając to do wzoru na ΔM:

ΔM = 2 * [(m + M)g - B] / g

ΔM = 2 * (m + M - B/g)

Teraz rozważmy, co się stanie, jeśli balon nie opada ze stałą prędkością, ale z przyspieszeniem. Wtedy sytuacja staje się bardziej skomplikowana. Musimy uwzględnić drugą zasadę dynamiki Newtona: F = ma, gdzie F to siła wypadkowa, m to masa, a a to przyspieszenie.

Jeśli balon opada z przyspieszeniem a, to równanie sił wygląda tak:

(m + M)g - B - Op = (m + M)a

W tym przypadku, siła ciężkości jest większa od sumy sił wyporu i oporu powietrza, dlatego balon przyspiesza w dół.

Po wyrzuceniu balastu ΔM, równanie sił (zakładając, że balon zaczyna się wznosić z przyspieszeniem a') wygląda tak:

B - (m + M - ΔM)g - Op = (m + M - ΔM)a'

Żeby balon zaczął się wznosić ze stałą prędkością, przyspieszenie a' musi być równe zero. Zatem:

B - (m + M - ΔM)g - Op = 0

(m + M - ΔM)g = B - Op

Teraz mamy dwa równania:

(m + M)g - B - Op = (m + M)a
(m + M - ΔM)g = B - Op

Chcemy wyznaczyć ΔM. Z pierwszego równania możemy wyznaczyć B + Op:

B + Op = (m + M)g - (m + M)a = (m + M)(g - a)

A z drugiego równania mamy B - Op. Aby wyznaczyć Op, odejmijmy drugie równanie od pierwszego:

(B + Op) - (B - Op) = (m + M)(g - a) - (m + M - ΔM)g

2Op = (m + M)g - (m + M)a - (m + M)g + ΔMg

2Op = - (m + M)a + ΔMg

ΔMg = 2Op + (m + M)a

ΔM = (2Op + (m + M)a) / g

Aby wyznaczyć Op, użyjemy równania (m + M)g - B - Op = (m + M)a

Op = (m + M)g - B - (m + M)a

Op = (m + M)(g - a) - B

Podstawiając to do wzoru na ΔM:

ΔM = (2 * [(m + M)(g - a) - B] + (m + M)a) / g

ΔM = (2(m + M)(g - a) - 2B + (m + M)a) / g

ΔM = (2(m + M)g - 2(m + M)a - 2B + (m + M)a) / g

ΔM = (2(m + M)g - (m + M)a - 2B) / g

ΔM = 2(m + M) - (m + M)a/g - 2B/g

ΔM = 2(m + M - B/g) - (m + M)a/g

H2: Wpływ Przyspieszenia na Obliczenia

Widzimy, że uwzględnienie przyspieszenia opadania balonu komplikuje obliczenia. Jeżeli balon opada z przyspieszeniem a, to musimy uwzględnić dodatkowy człon -(m + M)a/g w obliczeniach masy balastu do wyrzucenia. Im większe przyspieszenie, tym więcej balastu trzeba wyrzucić, aby balon zaczął się wznosić ze stałą prędkością. W praktyce, dokładne wyznaczenie siły oporu powietrza (Op) i przyspieszenia (a) może być trudne, dlatego często stosuje się metody prób i błędów, wyrzucając balast stopniowo i obserwując reakcję balonu.

H2: Uproszczenia i Założenia

W naszych rozważaniach dokonaliśmy pewnych uproszczeń. Założyliśmy, że objętość balonu jest stała, a siła wyporu nie zmienia się wraz z wysokością. Pomijamy również wpływ wiatru i zmian temperatury powietrza. W rzeczywistości, wszystkie te czynniki mogą wpływać na zachowanie balonu.

H2: Praktyczne Aspekty

W praktyce, piloci balonów nie przeprowadzają skomplikowanych obliczeń matematycznych w locie. Polegają na doświadczeniu i intuicji. Obserwują zachowanie balonu po wyrzuceniu małych porcji balastu i dostosowują swoje działania. Ważne jest również, aby monitorować wysokość i warunki atmosferyczne.

H2: Podsumowanie

Wyznaczenie masy balastu, którą należy wyrzucić, aby balon przestał opadać i zaczął się wznosić ze stałą prędkością, zależy od wielu czynników, w tym od masy balonu, masy balastu, siły wyporu, siły oporu powietrza oraz przyspieszenia opadania balonu. W idealnym przypadku, gdy balon opada ze stałą prędkością, wystarczy wyrzucić masę balastu równą podwojonej sile oporu powietrza podzielonej przez przyspieszenie ziemskie. Jednak w rzeczywistości, dokładne obliczenia mogą być trudne, dlatego często stosuje się metody prób i błędów.