2 Zasada Dynamiki Newtona Zadania

Czy zastanawiałeś się kiedyś, jak dokładnie obliczyć siłę potrzebną do rozpędzenia samochodu? Albo dlaczego lżejszy obiekt przyspiesza szybciej pod wpływem tej samej siły? Odpowiedź na te pytania kryje się w jednym z fundamentalnych praw fizyki: Drugiej Zasadzie Dynamiki Newtona. W tym artykule przyjrzymy się tej zasadzie w praktyce, rozwiązując różnorodne zadania, które pomogą Ci zrozumieć i wykorzystać ją w życiu codziennym.

Czym jest Druga Zasada Dynamiki Newtona?

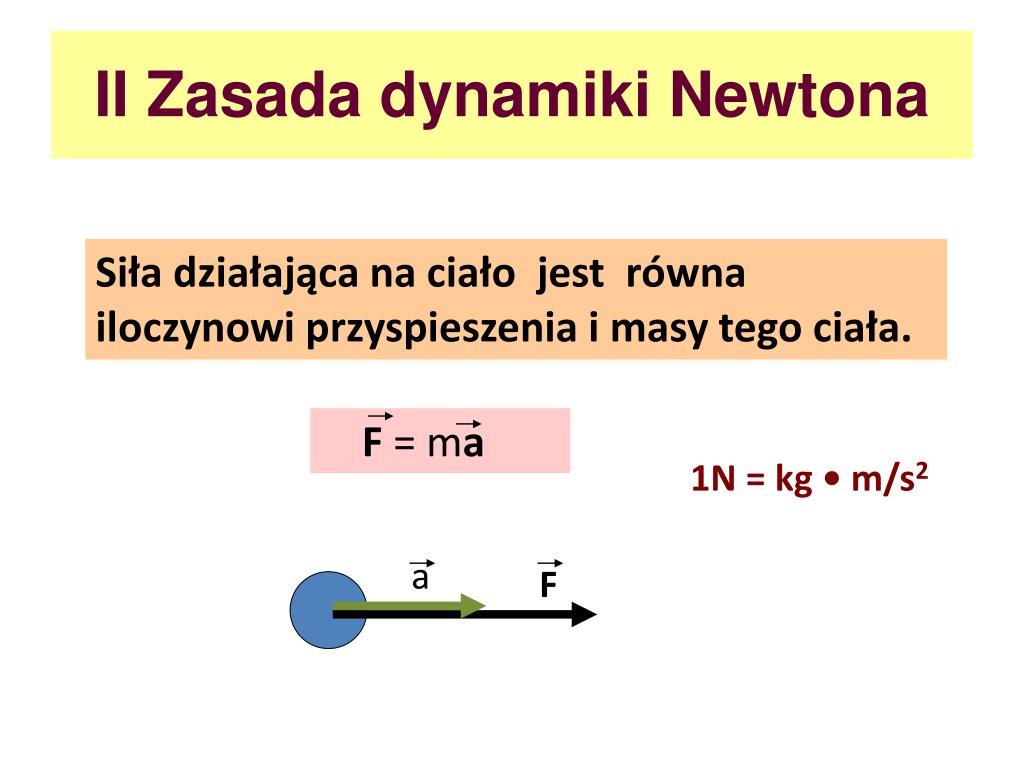
Druga Zasada Dynamiki Newtona, nazywana również prawem przyspieszenia, opisuje związek między siłą działającą na ciało, masą tego ciała i przyspieszeniem, które ono uzyskuje. Mówiąc prościej, im większa siła działa na ciało, tym większe jest jego przyspieszenie. Z kolei, im większa masa ciała, tym mniejsze będzie jego przyspieszenie przy tej samej sile.

Matematycznie zapisujemy to w następujący sposób:

F = m * a

Gdzie:

F to wypadkowa siła działająca na ciało (mierzona w Newtonach - N)
m to masa ciała (mierzona w kilogramach - kg)
a to przyspieszenie ciała (mierzone w metrach na sekundę kwadratową - m/s²)

Zrozumienie tej prostej równości otwiera drzwi do analizy ruchu wielu obiektów, od spadających jabłek po rakiety kosmiczne. Przejdźmy teraz do konkretnych przykładów, aby lepiej zrozumieć, jak stosować tę zasadę w praktyce.

Przykładowe Zadania i ich Rozwiązania

Oto kilka typowych zadań, które wykorzystują Drugą Zasadę Dynamiki Newtona:

Zadanie 1: Rozpędzanie wózka

Treść: Na wózek o masie 5 kg działa siła o wartości 10 N. Oblicz przyspieszenie wózka.

Rozwiązanie:

Zapisujemy dane: m = 5 kg, F = 10 N
Zapisujemy wzór: F = m * a
Przekształcamy wzór, aby obliczyć przyspieszenie: a = F / m
Podstawiamy dane: a = 10 N / 5 kg
Obliczamy: a = 2 m/s²

Odpowiedź: Przyspieszenie wózka wynosi 2 m/s².

Zadanie 2: Hamowanie samochodu

Treść: Samochód o masie 1200 kg hamuje z przyspieszeniem -3 m/s². Oblicz siłę hamowania.

Rozwiązanie:

Zapisujemy dane: m = 1200 kg, a = -3 m/s²
Zapisujemy wzór: F = m * a
Podstawiamy dane: F = 1200 kg * (-3 m/s²)
Obliczamy: F = -3600 N

Odpowiedź: Siła hamowania wynosi -3600 N. Znak minus oznacza, że siła działa przeciwnie do kierunku ruchu (czyli hamuje).

Zadanie 3: Pociąg z wagonami

Treść: Lokomotywa ciągnie trzy wagony o masie 20 ton każdy. Siła ciągu lokomotywy wynosi 120 kN. Oblicz przyspieszenie pociągu, zakładając, że pomijamy opory ruchu.

Rozwiązanie:

Zapisujemy dane: F = 120 kN = 120 000 N, masa jednego wagonu = 20 ton = 20 000 kg, liczba wagonów = 3
Obliczamy całkowitą masę pociągu: m = 3 * 20 000 kg = 60 000 kg
Zapisujemy wzór: F = m * a
Przekształcamy wzór, aby obliczyć przyspieszenie: a = F / m
Podstawiamy dane: a = 120 000 N / 60 000 kg
Obliczamy: a = 2 m/s²

Odpowiedź: Przyspieszenie pociągu wynosi 2 m/s².

Zadanie 4: Dwie siły działające na ciało

Treść: Na ciało o masie 2 kg działają dwie siły: F1 = 5 N w prawo i F2 = 3 N w lewo. Oblicz przyspieszenie ciała.

Rozwiązanie:

Zapisujemy dane: m = 2 kg, F1 = 5 N, F2 = -3 N (siła w lewo ma znak ujemny)
Obliczamy wypadkową siłę: F = F1 + F2 = 5 N - 3 N = 2 N
Zapisujemy wzór: F = m * a
Przekształcamy wzór, aby obliczyć przyspieszenie: a = F / m
Podstawiamy dane: a = 2 N / 2 kg
Obliczamy: a = 1 m/s²

Odpowiedź: Przyspieszenie ciała wynosi 1 m/s² w prawo.

Zadanie 5: Spadek swobodny z oporem powietrza (uproszczone)

Treść: Spadochroniarz o masie 80 kg spada. Siła oporu powietrza działająca na niego wynosi 600 N. Oblicz jego przyspieszenie. (Przyjmij g = 9.81 m/s²)

Rozwiązanie:

Zapisujemy dane: m = 80 kg, g = 9.81 m/s², F_oporu = 600 N
Obliczamy siłę ciężkości (siłę grawitacji): F_grawitacji = m * g = 80 kg * 9.81 m/s² = 784.8 N
Obliczamy wypadkową siłę: F = F_grawitacji - F_oporu = 784.8 N - 600 N = 184.8 N
Zapisujemy wzór: F = m * a
Przekształcamy wzór, aby obliczyć przyspieszenie: a = F / m
Podstawiamy dane: a = 184.8 N / 80 kg
Obliczamy: a = 2.31 m/s²

Odpowiedź: Przyspieszenie spadochroniarza wynosi 2.31 m/s² w dół.

Wskazówki i Częste Błędy

Uważaj na jednostki: Upewnij się, że wszystkie dane są wyrażone w odpowiednich jednostkach (kg, m, s, N).
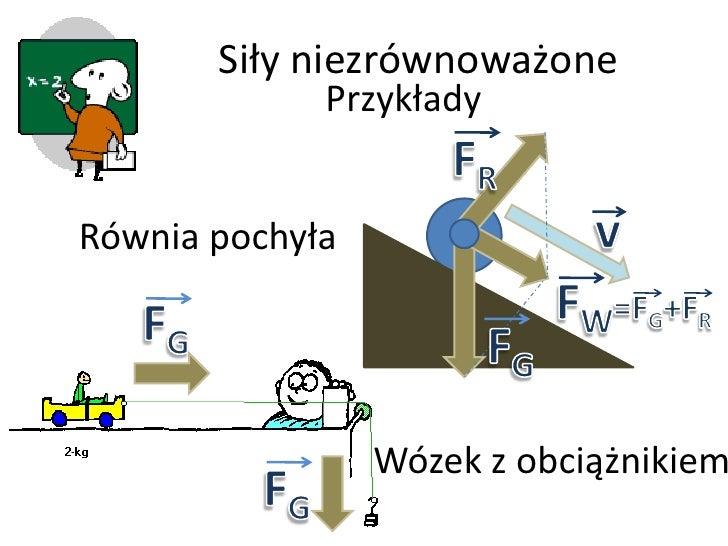
Wektorowa natura siły: Siła jest wektorem, co oznacza, że ma zarówno wartość, jak i kierunek. Uwzględniaj kierunek sił przy obliczaniu wypadkowej.
Siła wypadkowa: Pamiętaj, że w równaniu F = m * a, F to wypadkowa siła działająca na ciało, czyli suma wszystkich sił.
Opory ruchu: Często w zadaniach upraszcza się sytuację, pomijając opory ruchu (tarcie, opór powietrza). W rzeczywistości, te siły zawsze występują i wpływają na ruch ciała.
Zrozumienie pojęć: Upewnij się, że rozumiesz różnicę między masą a ciężarem. Masa to miara ilości materii w ciele, a ciężar to siła, z jaką Ziemia przyciąga ciało.

Druga Zasada Dynamiki w Życiu Codziennym

Druga Zasada Dynamiki Newtona ma ogromne znaczenie w wielu dziedzinach życia. Oto kilka przykładów:

Sport: Rozumienie tej zasady jest kluczowe w wielu sportach, takich jak rzut oszczepem, pchnięcie kulą czy skoki narciarskie. Sportowcy starają się maksymalizować siłę, aby uzyskać jak największe przyspieszenie i osiągnąć lepsze wyniki.
Inżynieria: Inżynierowie wykorzystują Druga Zasadę Dynamiki przy projektowaniu pojazdów, budynków, mostów i innych konstrukcji. Muszą obliczyć siły działające na te obiekty i zapewnić, że są one wystarczająco wytrzymałe.
Transport: Projektowanie samochodów, pociągów i samolotów wymaga precyzyjnego obliczania sił i przyspieszeń, aby zapewnić bezpieczeństwo i wydajność.
Medycyna: Analiza biomechaniki ruchu człowieka, na przykład podczas chodzenia czy biegania, również opiera się na Drugiej Zasadzie Dynamiki.

Wyobraź sobie, że pchasz ciężki wózek z zakupami. Im bardziej się wysilisz (większa siła), tym szybciej wózek przyspieszy. Z drugiej strony, jeśli wózek jest bardzo pełny (duża masa), będzie trudniej go rozpędzić przy tej samej sile. To właśnie Druga Zasada Dynamiki w akcji! Pomyśl o tym następnym razem, gdy będziesz przesuwał meble albo jechał na rowerze.

Podsumowanie

Druga Zasada Dynamiki Newtona to potężne narzędzie, które pozwala nam zrozumieć i opisać ruch ciał. Dzięki niej możemy obliczać przyspieszenia, siły i masy, a także analizować wiele zjawisk fizycznych, które zachodzą wokół nas. Rozwiązując zadania i analizując przykłady z życia codziennego, możesz lepiej zrozumieć to fundamentalne prawo i wykorzystać je w praktyce.

Mamy nadzieję, że ten artykuł pomógł Ci lepiej zrozumieć Drugą Zasadę Dynamiki Newtona i jej zastosowania. Pamiętaj, że kluczem do sukcesu jest praktyka! Rozwiązuj zadania, analizuj przykłady i nie bój się pytać, jeśli masz wątpliwości. Powodzenia w dalszej nauce fizyki!