Wzory Na Ostrosłupy I Graniastosłupy

Zmagasz się z obliczaniem objętości i pola powierzchni ostrosłupów i graniastosłupów? Nie jesteś sam! Wielu uczniów i studentów matematyki (a także inżynierów!) napotyka na trudności z tymi zagadnieniami. Kluczem do sukcesu jest zrozumienie podstawowych wzorów i umiejętność ich poprawnego zastosowania. Ten artykuł ma na celu rozwianie Twoich wątpliwości i pomóc Ci opanować te zagadnienia. Pamiętaj, że dobra znajomość tych figur geometrycznych przydaje się nie tylko na lekcjach matematyki, ale również w życiu codziennym, np. przy planowaniu przestrzeni czy obliczaniu potrzebnych materiałów budowlanych.

Graniastosłupy - Podstawowe Wzory

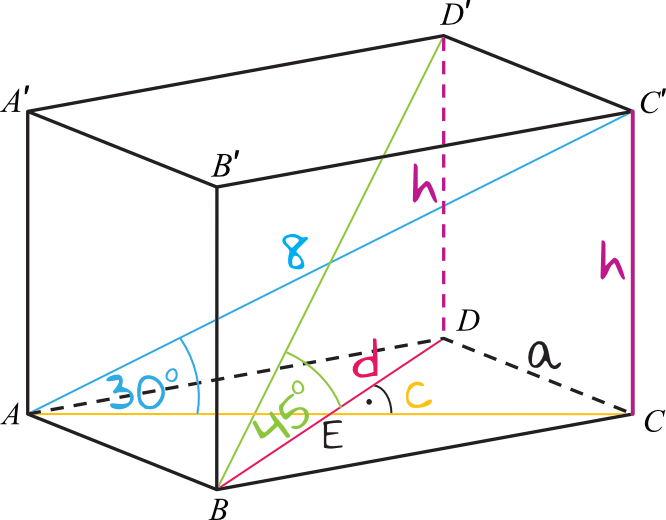
Graniastosłup to wielościan, którego dwie ściany (podstawy) są przystającymi wielokątami, leżącymi w równoległych płaszczyznach, a pozostałe ściany (ściany boczne) są równoległobokami. Podstawowe rodzaje graniastosłupów to graniastosłupy proste i pochyłe. Skupimy się głównie na graniastosłupach prostych, które są najczęściej spotykane w zadaniach.

Wzór na objętość graniastosłupa (V):

V = Pp * H

Gdzie:

V - objętość graniastosłupa
Pp - pole podstawy graniastosłupa (pole figury geometrycznej, która stanowi podstawę, np. trójkąta, kwadratu, pięciokąta, etc.)
H - wysokość graniastosłupa (odległość między płaszczyznami podstaw)

Wzór na pole powierzchni całkowitej graniastosłupa (Pc):

Pc = 2Pp + Pb

Gdzie:

Pc - pole powierzchni całkowitej graniastosłupa
Pp - pole podstawy graniastosłupa (jak wyżej)
Pb - pole powierzchni bocznej graniastosłupa (suma pól wszystkich ścian bocznych)

Przykłady graniastosłupów i obliczanie ich pól i objętości

1. Graniastosłup prosty trójkątny: Wyobraź sobie namiot w kształcie graniastosłupa prostego trójkątnego. Jego podstawą jest trójkąt. Jeśli podstawa trójkąta ma długość a, a wysokość tego trójkąta wynosi h, to pole podstawy Pp = (a * h) / 2. Pole powierzchni bocznej to suma pól trzech prostokątów (ściany namiotu). Jeśli wysokość graniastosłupa (czyli długość namiotu) wynosi H, a boki trójkąta w podstawie mają długości a, b, c, to pole powierzchni bocznej Pb = aH + bH + cH. Objętość obliczamy mnożąc pole podstawy przez wysokość graniastosłupa, czyli V = ((a * h) / 2) * H.

2. Graniastosłup prosty czworokątny (prostopadłościan): Najprostszy przykład to pudełko od butów. Jeśli jego boki mają długości a, b, c, to pole powierzchni całkowitej wynosi Pc = 2(ab + bc + ac), a objętość V = abc.

3. Graniastosłup prosty sześciokątny: Podstawą jest sześciokąt foremny. Pole sześciokąta foremnego o boku a wynosi Pp = (3√3 * a^2) / 2. Jeśli wysokość graniastosłupa wynosi H, to pole powierzchni bocznej Pb = 6aH, a objętość V = ((3√3 * a^2) / 2) * H.

Ostrosłupy - Wzory na Objętość i Pole Powierzchni

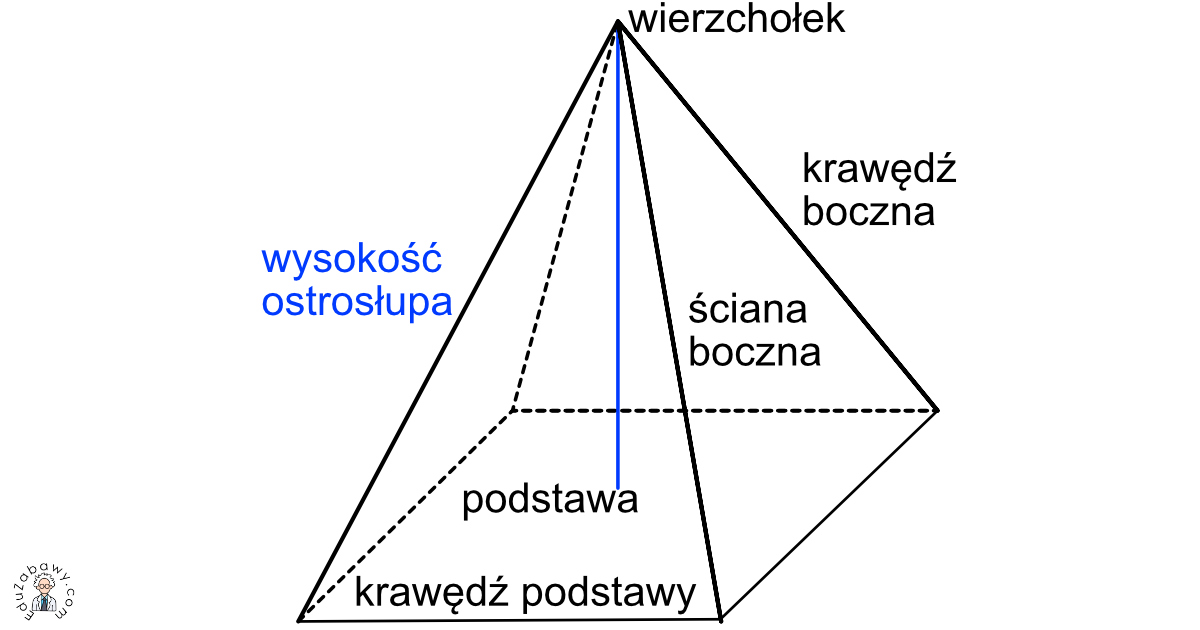
Ostrosłup to wielościan, którego jedna ściana (podstawa) jest wielokątem, a pozostałe ściany (ściany boczne) są trójkątami o wspólnym wierzchołku (wierzchołku ostrosłupa). Podobnie jak w przypadku graniastosłupów, rozróżniamy ostrosłupy proste i pochyłe, ale skupimy się na ostrosłupach prostych, gdzie spodek wysokości ostrosłupa pokrywa się ze środkiem okręgu opisanego na podstawie.

Wzór na objętość ostrosłupa (V):

V = (1/3) * Pp * H

Gdzie:

V - objętość ostrosłupa
Pp - pole podstawy ostrosłupa
H - wysokość ostrosłupa (odległość od wierzchołka do płaszczyzny podstawy)

Wzór na pole powierzchni całkowitej ostrosłupa (Pc):

Pc = Pp + Pb

Gdzie:

Pc - pole powierzchni całkowitej ostrosłupa
Pp - pole podstawy ostrosłupa
Pb - pole powierzchni bocznej ostrosłupa (suma pól wszystkich ścian bocznych, czyli trójkątów)

Przykłady ostrosłupów i obliczanie ich pól i objętości

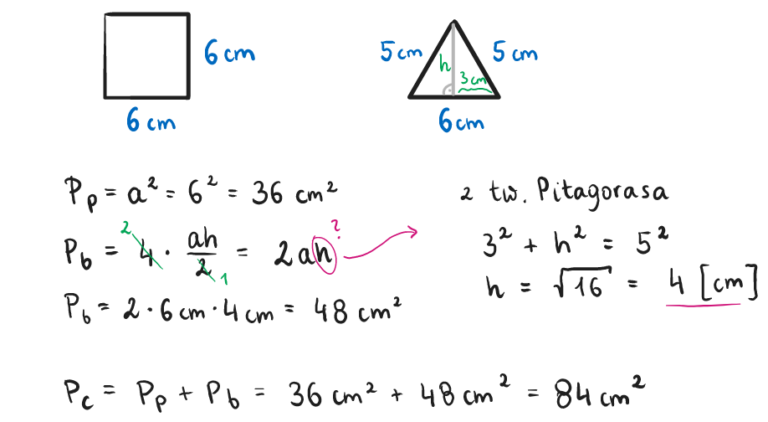
1. Ostrosłup prawidłowy czworokątny: Jego podstawą jest kwadrat. Jeśli bok kwadratu ma długość a, to pole podstawy Pp = a^2. Ściany boczne to trójkąty równoramienne. Aby obliczyć pole powierzchni bocznej, potrzebujemy wysokości ściany bocznej (wysokości trójkąta poprowadzonej z wierzchołka ostrosłupa do środka boku kwadratu). Oznaczmy tę wysokość jako hs. Wtedy pole powierzchni bocznej Pb = 4 * (1/2) * a * hs = 2 * a * hs. Objętość obliczamy, korzystając ze wzoru V = (1/3) * a^2 * H, gdzie H to wysokość ostrosłupa.

2. Ostrosłup prawidłowy trójkątny (czworościan foremny): Wszystkie jego ściany są trójkątami równobocznymi. Jeśli bok trójkąta ma długość a, to pole trójkąta Pp = (a^2 * √3) / 4. Pole powierzchni całkowitej czworościanu foremnego to Pc = 4 * Pp = a^2 * √3. Wysokość czworościanu foremnego można obliczyć ze wzoru H = a√(2/3), a objętość V = (a^3 * √2) / 12.

3. Ostrosłup prawidłowy sześciokątny: Podstawą jest sześciokąt foremny, jak w przypadku graniastosłupa. Pole sześciokąta foremnego o boku a wynosi Pp = (3√3 * a^2) / 2. Ściany boczne to trójkąty równoramienne. Obliczenie pola powierzchni bocznej i objętości wymaga znajomości wysokości ściany bocznej (hs) i wysokości ostrosłupa (H), które często są podane w zadaniu lub można je obliczyć, korzystając z twierdzenia Pitagorasa.

Praktyczne wskazówki i triki

1. Rysunek to podstawa: Zawsze narysuj sobie ostrosłup lub graniastosłup. Oznaczenie danych na rysunku ułatwi Ci zidentyfikowanie, które wymiary są Ci potrzebne do obliczeń.

2. Twierdzenie Pitagorasa: Bardzo często w zadaniach dotyczących ostrosłupów i graniastosłupów trzeba skorzystać z twierdzenia Pitagorasa, aby obliczyć brakujące długości (np. wysokość ściany bocznej ostrosłupa).

3. Rozpoznawanie figur w podstawie: Upewnij się, że znasz wzory na pola powierzchni podstawowych figur geometrycznych, takich jak trójkąt, kwadrat, prostokąt, sześciokąt foremny, etc. To kluczowe do obliczenia pola podstawy graniastosłupa lub ostrosłupa.

4. Jednostki: Zawsze pamiętaj o podawaniu jednostek! Objętość wyrażamy w jednostkach sześciennych (np. cm³, m³), a pole powierzchni w jednostkach kwadratowych (np. cm², m²).

5. Sprawdzanie odpowiedzi: Po obliczeniu objętości lub pola powierzchni, zastanów się, czy wynik jest sensowny. Czy objętość jest dodatnia? Czy pole powierzchni jest większe od zera? Czy wynik ma realną wartość w kontekście zadania?

6. Zadania, zadania i jeszcze raz zadania: Najlepszym sposobem na opanowanie wzorów na ostrosłupy i graniastosłupy jest rozwiązywanie zadań. Im więcej zadań rozwiążesz, tym lepiej zrozumiesz, jak stosować te wzory w praktyce.

7. Wykorzystaj narzędzia online: Dostępne są kalkulatory online, które mogą pomóc w sprawdzeniu poprawności obliczeń. Pamiętaj jednak, żeby nie polegać na nich całkowicie! Staraj się najpierw samodzielnie rozwiązać zadanie, a następnie sprawdź wynik za pomocą kalkulatora.

Pamiętaj, że opanowanie wzorów na ostrosłupy i graniastosłupy wymaga czasu i praktyki. Nie zrażaj się trudnościami i regularnie rozwiązuj zadania. Powodzenia!