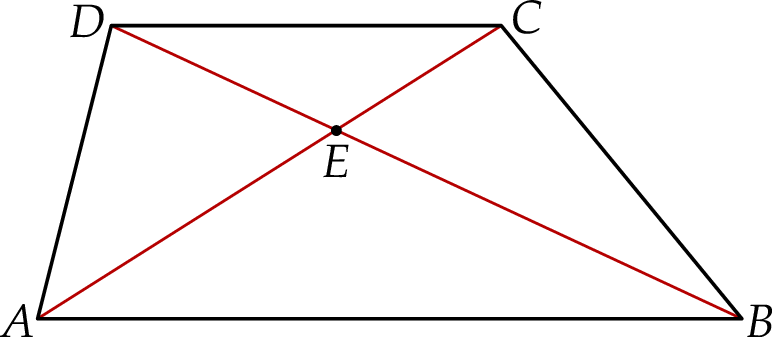
W Trapezie Abcd O Podstawach Ab I Cd

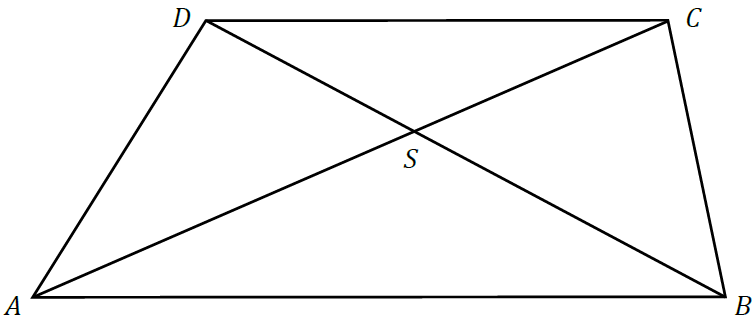
W geometrii, trapez jest czworokątem, który ma co najmniej jedną parę boków równoległych. Te równoległe boki nazywamy podstawami trapezu, a pozostałe dwa boki to ramiona. Kiedy mówimy o trapezie ABCD o podstawach AB i CD, precyzujemy, które boki są równoległe i stanowią podstawy figury. Ten artykuł zgłębi własności, charakterystyki i zastosowania trapezu ABCD z wyraźnie określonymi podstawami AB i CD.

Definicja i podstawowe właściwości

Trapez ABCD o podstawach AB i CD definiuje się jako czworokąt, w którym bok AB jest równoległy do boku CD (AB || CD). Boki AD i BC to ramiona trapezu. Ważne jest, aby pamiętać, że w ogólnym przypadku ramiona nie są równoległe ani równe.

Rodzaje trapezów

Trapezy można podzielić na kilka rodzajów, w zależności od dodatkowych warunków, jakie spełniają:

• Trapez równoramienny: Jest to trapez, którego ramiona (AD i BC) są równej długości. Dodatkowo, kąty przy każdej z podstaw są równe.
• Trapez prostokątny: Jest to trapez, w którym jedno z ramion jest prostopadłe do podstaw. Innymi słowy, trapez prostokątny ma co najmniej jeden kąt prosty.
• Trapez różnoboczny: Jest to trapez, który nie jest ani równoramienny, ani prostokątny. Wszystkie jego boki i kąty są różne (z wyjątkiem konieczności równoległości podstaw).

Rozróżnienie tych typów trapezów jest istotne, ponieważ każdy z nich ma specyficzne właściwości geometryczne, które wpływają na sposób rozwiązywania zadań i obliczania różnych wielkości.

Kluczowe twierdzenia i wzory

Zrozumienie trapezów wymaga znajomości pewnych kluczowych twierdzeń i wzorów:

Wysokość trapezu

Wysokość trapezu (oznaczana zwykle jako h) to odległość między podstawami AB i CD. Jest to długość odcinka prostopadłego, poprowadzonego z dowolnego punktu na jednej podstawie do drugiej podstawy.

Pole trapezu

Pole trapezu oblicza się za pomocą wzoru:

P = (a + b) * h / 2

Gdzie:

• P to pole trapezu
• a to długość podstawy AB
• b to długość podstawy CD
• h to wysokość trapezu

Wzór ten wynika z faktu, że trapez można podzielić na dwa trójkąty i prostokąt (lub dwa trójkąty i równoległobok) i zsumować ich pola. Prostota tego wzoru czyni go niezwykle użytecznym w praktycznych zastosowaniach.

Linia środkowa trapezu

Linia środkowa trapezu to odcinek łączący środki ramion (AD i BC). Jest ona równoległa do podstaw i jej długość jest równa średniej arytmetycznej długości podstaw:

m = (a + b) / 2

Gdzie:

• m to długość linii środkowej
• a to długość podstawy AB
• b to długość podstawy CD

Linia środkowa ma istotne właściwości. Dzieli trapez na dwa mniejsze trapezy o równych wysokościach. Znajomość jej długości często ułatwia obliczenia.

Zastosowania w realnym świecie

Trapezy, w tym trapez ABCD o podstawach AB i CD, pojawiają się w wielu miejscach w otaczającym nas świecie. Ich właściwości znajdują zastosowanie w różnych dziedzinach.

Architektura i budownictwo

Elementy trapezoidalne są często wykorzystywane w architekturze i budownictwie. Dachy budynków, okna, mosty - to tylko niektóre przykłady. Na przykład, konstrukcja dachu może wykorzystywać trapezy do zapewnienia odpowiedniego spadu i odprowadzania wody. Mosty wiszące często wykorzystują trapezoidalne segmenty w swoich konstrukcjach nośnych.

Inżynieria

W inżynierii, trapezy znajdują zastosowanie w projektowaniu różnego rodzaju urządzeń i konstrukcji. Na przykład, przekroje rowów melioracyjnych często mają kształt trapezu, co zapewnia optymalny przepływ wody i stabilność brzegów. W mechanice, trapezy mogą być wykorzystywane w konstrukcji dźwigni i innych mechanizmów.

Grafika komputerowa i projektowanie

W grafice komputerowej, trapezy są używane do tworzenia perspektywy i symulowania trójwymiarowych obiektów na dwuwymiarowym ekranie. Teksturowanie powierzchni i renderowanie scen wykorzystuje transformacje trapezoidalne do odwzorowania obrazów.

Geodezja i kartografia

W geodezji i kartografii, trapezy mogą być wykorzystywane do przybliżania powierzchni nieregularnych obszarów. Podział terenu na trapezy pozwala na oszacowanie powierzchni działek i gruntów.

Przykłady obliczeniowe

Rozważmy trapez ABCD, w którym podstawa AB ma długość 10 cm, podstawa CD ma długość 6 cm, a wysokość trapezu wynosi 4 cm.

Obliczanie pola

Aby obliczyć pole trapezu, korzystamy ze wzoru:

P = (a + b) * h / 2 = (10 cm + 6 cm) * 4 cm / 2 = 16 cm * 4 cm / 2 = 32 cm²

Zatem pole trapezu ABCD wynosi 32 cm².

Obliczanie długości linii środkowej

Aby obliczyć długość linii środkowej, korzystamy ze wzoru:

m = (a + b) / 2 = (10 cm + 6 cm) / 2 = 16 cm / 2 = 8 cm

Zatem długość linii środkowej trapezu ABCD wynosi 8 cm.

Trudniejsze zadania i zastosowania w dowodach

Trapezy pojawiają się również w bardziej zaawansowanych zadaniach geometrycznych i dowodach. Przykładowo, można rozważać podział trapezu na mniejsze figury, dowodzenie własności linii łączącej środki ramion, czy też wykorzystywanie twierdzenia Talesa do rozwiązywania problemów związanych z proporcjami w trapezie.

W dowodach geometrycznych, często korzysta się z własności kątów, równoległości i kongruencji trójkątów, które powstają w wyniku podziału trapezu. Wykorzystanie linii pomocniczych, takich jak wysokości czy przekątne, może ułatwić rozwiązanie trudniejszych zadań.

Podsumowanie i wnioski

Trapez ABCD o podstawach AB i CD to podstawowa figura geometryczna, która ma szerokie zastosowanie w różnych dziedzinach. Zrozumienie jego definicji, właściwości i wzorów jest kluczowe dla rozwiązywania problemów geometrycznych i praktycznych. Różne typy trapezów (równoramienne, prostokątne, różnoboczne) wymagają indywidualnego podejścia i znajomości specyficznych cech.

Zachęcamy do dalszego zgłębiania wiedzy o trapezach i ich zastosowaniach. Rozwiązywanie różnorodnych zadań i analiza przypadków praktycznych pozwoli na pełne zrozumienie tej fascynującej figury geometrycznej. Spróbuj samodzielnie znaleźć przykłady trapezów w swoim otoczeniu i zastanów się, jakie właściwości trapezu są wykorzystywane w danym zastosowaniu.