Ułamki Dziesiętne Klasa 4 Sprawdzian

Witajcie drodzy uczniowie klasy 4! Dzisiaj porozmawiamy o ułamkach dziesiętnych. Temat ten może wydawać się na początku trochę skomplikowany, ale obiecuję, że po przeczytaniu tego artykułu, ułamki dziesiętne nie będą miały przed Wami żadnych tajemnic. Przygotujemy się wspólnie do sprawdzianu z ułamków dziesiętnych, omawiając definicje, przykłady i zadania praktyczne.
Co to są ułamki dziesiętne?
Ułamek dziesiętny to sposób zapisu liczby, która nie jest liczbą całkowitą. Zamiast używać kreski ułamkowej, jak w zwykłych ułamkach (np. 1/2), używamy przecinka. Liczby po przecinku oznaczają części mniejsze od 1, podzielone na dziesiąte, setne, tysięczne itd.
Przykłady ułamków dziesiętnych:
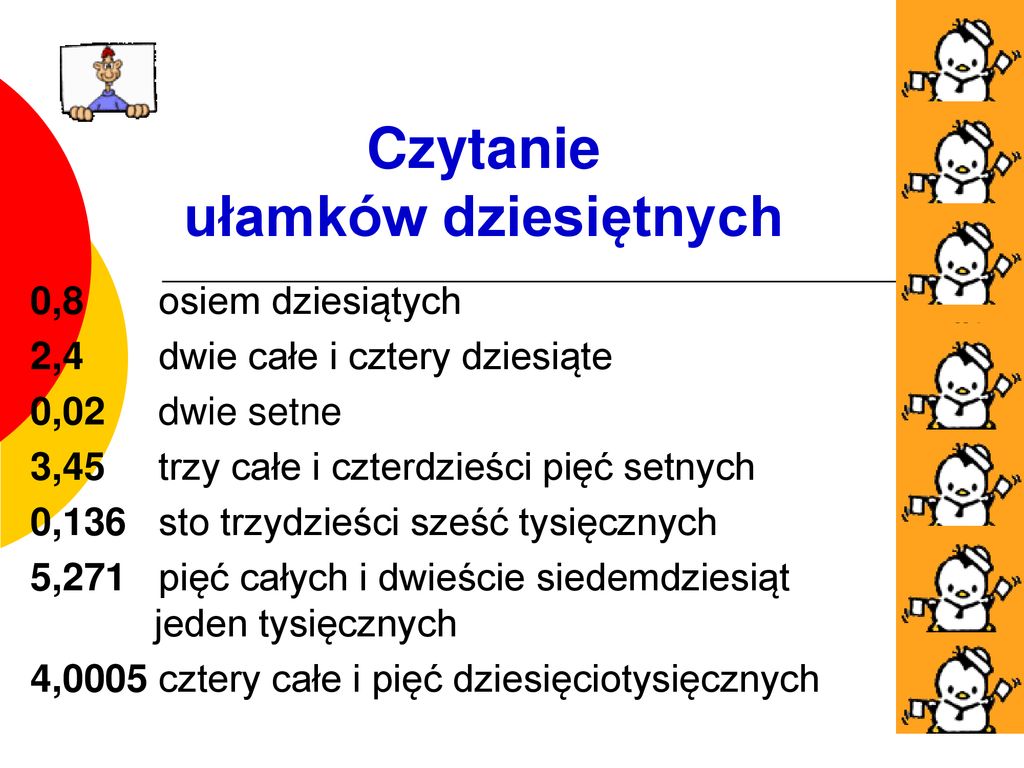
- 0,5 (zero i pięć dziesiątych)
- 1,25 (jeden i dwadzieścia pięć setnych)
- 3,01 (trzy i jeden setna)
- 0,750 (zero i siedemset pięćdziesiąt tysięcznych) – zauważ, że 0 na końcu nie zmienia wartości
Wyobraźcie sobie, że macie tabliczkę czekolady podzieloną na 10 równych części. Jeśli zjecie 5 z tych części, to zjedliście 0,5 tabliczki. A jeśli podzielimy tabliczkę na 100 części i zjecie 25 części, to zjedliście 0,25 tabliczki.
Części ułamka dziesiętnego
Każdy ułamek dziesiętny składa się z kilku ważnych części:
- Część całkowita: To liczba znajdująca się przed przecinkiem. Na przykład, w liczbie 3,14 częścią całkowitą jest 3.
- Przecinek: Oddziela część całkowitą od części ułamkowej.
- Część ułamkowa: To liczby znajdujące się po przecinku. Każda cyfra po przecinku ma swoją wartość:
- Pierwsza cyfra po przecinku oznacza dziesiąte części (np. 0,1 to jedna dziesiąta).
- Druga cyfra po przecinku oznacza setne części (np. 0,01 to jedna setna).
- Trzecia cyfra po przecinku oznacza tysięczne części (np. 0,001 to jedna tysięczna).
Spójrzmy na przykład 12,345. Tutaj:
- Część całkowita to 12.
- 3 to trzy dziesiąte (0,3).
- 4 to cztery setne (0,04).
- 5 to pięć tysięcznych (0,005).
Zapisywanie ułamków zwykłych jako dziesiętne
Niektóre ułamki zwykłe możemy łatwo zamienić na ułamki dziesiętne. Najprościej jest, gdy ułamek zwykły ma w mianowniku 10, 100, 1000 itd. Na przykład:
- 3/10 = 0,3
- 25/100 = 0,25
- 17/1000 = 0,017
Co, jeśli mianownik nie jest 10, 100 lub 1000? Czasami możemy pomnożyć licznik i mianownik przez odpowiednią liczbę, aby otrzymać mianownik równy 10, 100 lub 1000. Na przykład:
Weźmy ułamek 1/2. Możemy pomnożyć licznik i mianownik przez 5:
(1 * 5) / (2 * 5) = 5/10 = 0,5
Podobnie, dla ułamka 1/4:
(1 * 25) / (4 * 25) = 25/100 = 0,25
Nie wszystkie ułamki zwykłe da się tak łatwo zamienić na ułamki dziesiętne. Czasami potrzebne są bardziej zaawansowane metody (dzielenie pisemne), ale to już temat na inną lekcję.
Porównywanie ułamków dziesiętnych
Aby porównać ułamki dziesiętne, najpierw porównujemy ich części całkowite. Jeśli części całkowite są różne, to ułamek z większą częścią całkowitą jest większy. Na przykład:
- 3,2 > 2,9 (bo 3 > 2)
Jeśli części całkowite są takie same, porównujemy cyfry po przecinku, zaczynając od dziesiątych, potem setnych, tysięcznych itd. Na przykład:
- 1,52 > 1,48 (bo 5 > 4)
- 2,315 < 2,320 (bo 1 < 2 w setnych częściach)
Pamiętajcie, że możemy dopisywać zera na końcu ułamka dziesiętnego bez zmiany jego wartości. Na przykład:
- 0,5 = 0,50 = 0,500
Dzięki temu łatwiej jest porównywać ułamki, które mają różną liczbę cyfr po przecinku. Na przykład, aby porównać 0,3 i 0,27, możemy dopisać zero do 0,3, otrzymując 0,30. Wtedy łatwo widzimy, że 0,30 > 0,27.
Dodawanie i odejmowanie ułamków dziesiętnych
Aby dodać lub odjąć ułamki dziesiętne, musimy upewnić się, że przecinki są ustawione jeden pod drugim. Następnie dodajemy lub odejmujemy tak jak zwykłe liczby, pamiętając o przepisaniu przecinka w wyniku.
Przykład dodawania:
1,25
+ 0,75
-------
2,00
Przykład odejmowania:
3,50
- 1,25
-------
2,25
Jeśli jeden ułamek ma mniej cyfr po przecinku niż drugi, możemy dopisać zera, aby wyrównać liczbę cyfr. Na przykład, aby dodać 2,5 i 1,23, możemy zapisać 2,5 jako 2,50:
2,50
+ 1,23
-------
3,73
Praktyczne zastosowanie ułamków dziesiętnych
Ułamki dziesiętne są bardzo przydatne w życiu codziennym. Używamy ich, gdy mierzymy długość (np. 1,75 metra), wagę (np. 0,5 kg), temperaturę (np. 36,6 stopni Celsjusza) i pieniądze (np. 2,50 zł).
Na przykład, jeśli kupujecie w sklepie jabłka po 2,80 zł za kilogram i kupujecie 0,5 kg, to zapłacicie:
2,80 zł/kg * 0,5 kg = 1,40 zł
Przygotowanie do sprawdzianu
Aby dobrze przygotować się do sprawdzianu z ułamków dziesiętnych, warto:
- Powtórzyć definicje: co to jest ułamek dziesiętny, część całkowita, część ułamkowa, dziesiąte, setne, tysięczne.
- Poćwiczyć zamianę ułamków zwykłych na dziesiętne (szczególnie tych z mianownikami 10, 100, 1000).
- Poćwiczyć porównywanie ułamków dziesiętnych.
- Poćwiczyć dodawanie i odejmowanie ułamków dziesiętnych.
- Rozwiązać zadania tekstowe, w których trzeba użyć ułamków dziesiętnych.
Pamiętajcie, że praktyka czyni mistrza! Im więcej zadań rozwiążecie, tym lepiej zrozumiecie ułamki dziesiętne i tym pewniej będziecie się czuli na sprawdzianie. Powodzenia!