Trójkąty 30 60 90 I 45 45 90 Zadania

Witaj! Znasz już pewnie podstawy geometrii i wiesz czym jest trójkąt. Ale czy wiesz, że niektóre trójkąty prostokątne są wyjątkowe i mają specjalne właściwości, które ułatwiają rozwiązywanie zadań? Mówimy o trójkątach 30-60-90 i 45-45-90. Przyjrzyjmy się im bliżej!

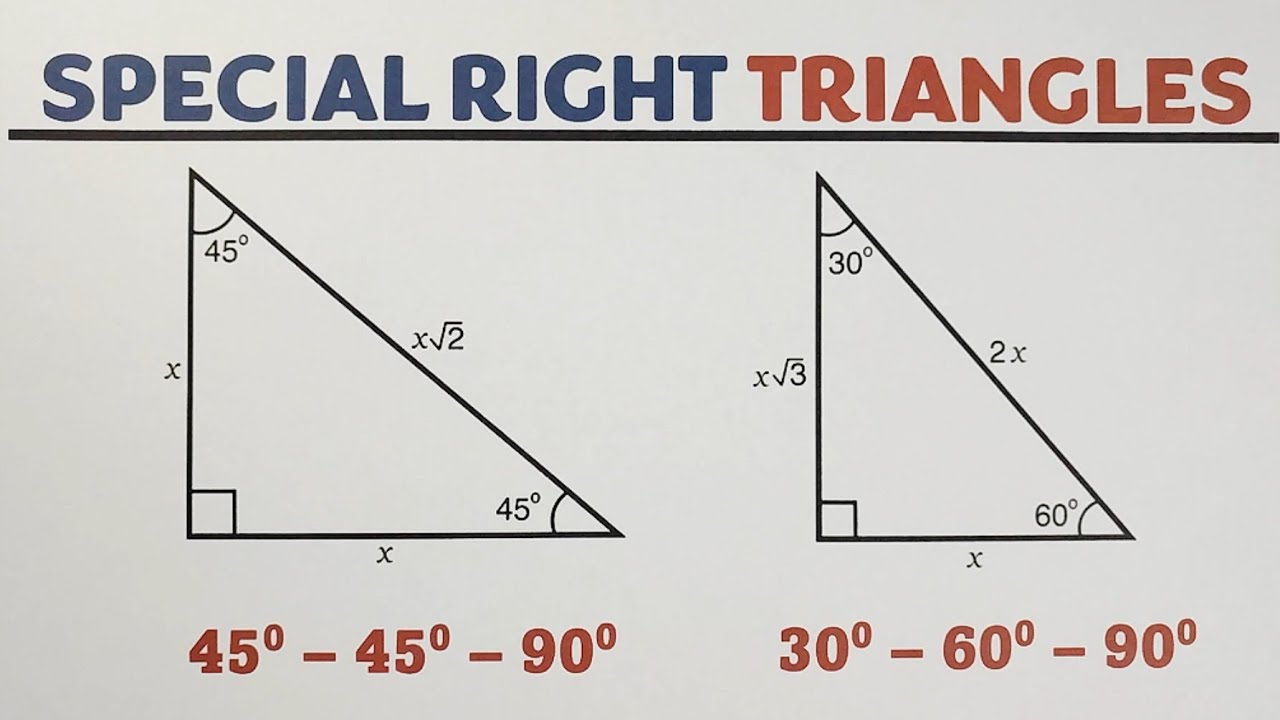
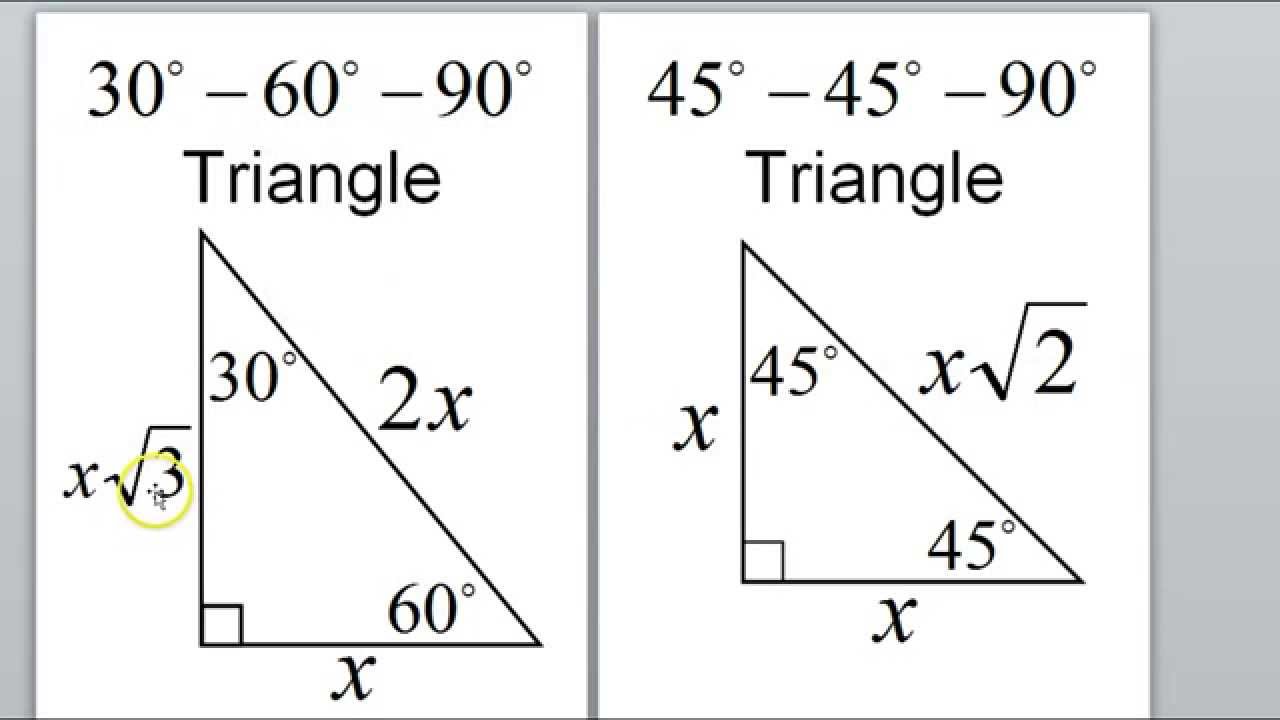
Trójkąt 30-60-90: Tajemnice połowy trójkąta równobocznego

Wyobraź sobie trójkąt równoboczny. Ma on trzy równe boki i trzy równe kąty, każdy po 60 stopni. Teraz wyobraź sobie, że przecinasz go na pół, wzdłuż wysokości (linia prostopadła do podstawy, przechodząca przez wierzchołek). Co otrzymasz? Dwa identyczne trójkąty prostokątne! Każdy z nich ma kąty: 30 stopni, 60 stopni i 90 stopni. Otóż to! Właśnie tak powstaje trójkąt 30-60-90.

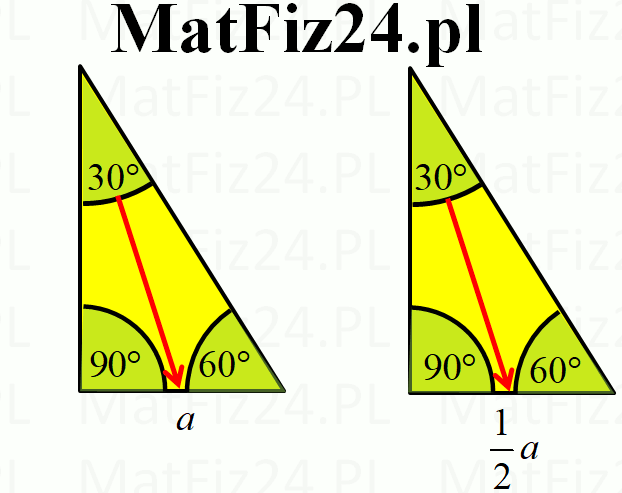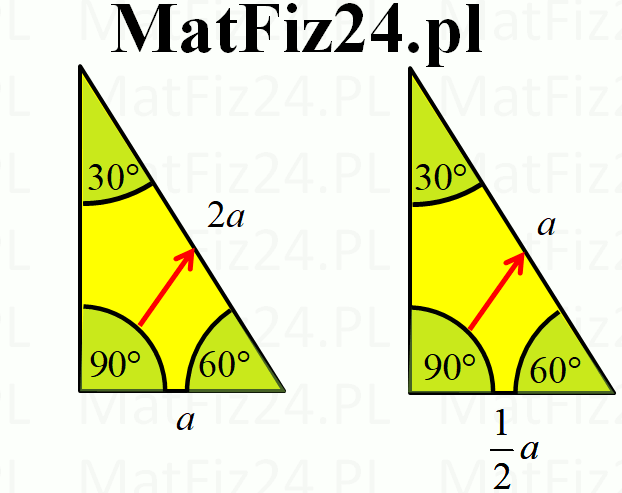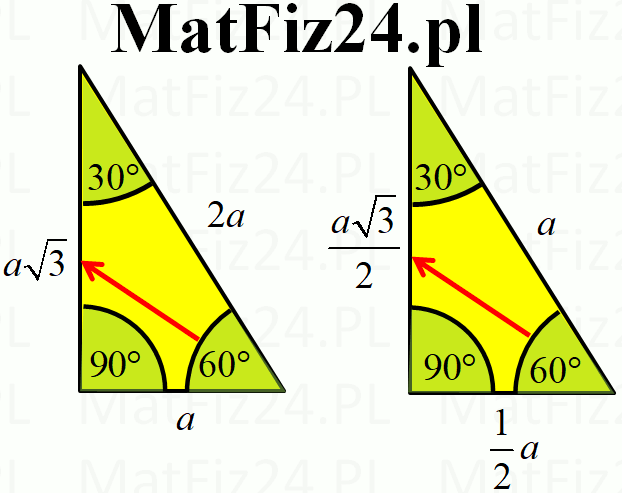
Teraz, co jest w nim takiego specjalnego? Otóż, stosunek długości boków w takim trójkącie jest zawsze taki sam. Jeśli długość najkrótszego boku (tego naprzeciwko kąta 30 stopni) oznaczysz jako 'a', to:

• Przeciwprostokątna (najdłuższy bok, naprzeciwko kąta 90 stopni) będzie miała długość 2a.
• Drugi bok (ten naprzeciwko kąta 60 stopni) będzie miał długość a√3.

Zauważ, że najkrótszy bok jest połową przeciwprostokątnej! To kluczowa obserwacja, która bardzo ułatwia rozwiązywanie zadań.

Przykład: Załóżmy, że najkrótszy bok trójkąta 30-60-90 ma długość 5 cm. Wtedy przeciwprostokątna ma długość 2 * 5 = 10 cm, a drugi bok ma długość 5√3 cm. Proste, prawda?

Zastosowania w życiu codziennym

Gdzie możemy spotkać trójkąty 30-60-90 w życiu? Na przykład, podczas projektowania ramp dla wózków inwalidzkich. Architekci często wykorzystują te proporcje, aby zapewnić odpowiedni kąt nachylenia. Innym przykładem są narzędzia pomiarowe, takie jak ekierki – często zawierają kąty 30 i 60 stopni, co ułatwia rysowanie linii prostopadłych i nachylonych pod odpowiednim kątem.

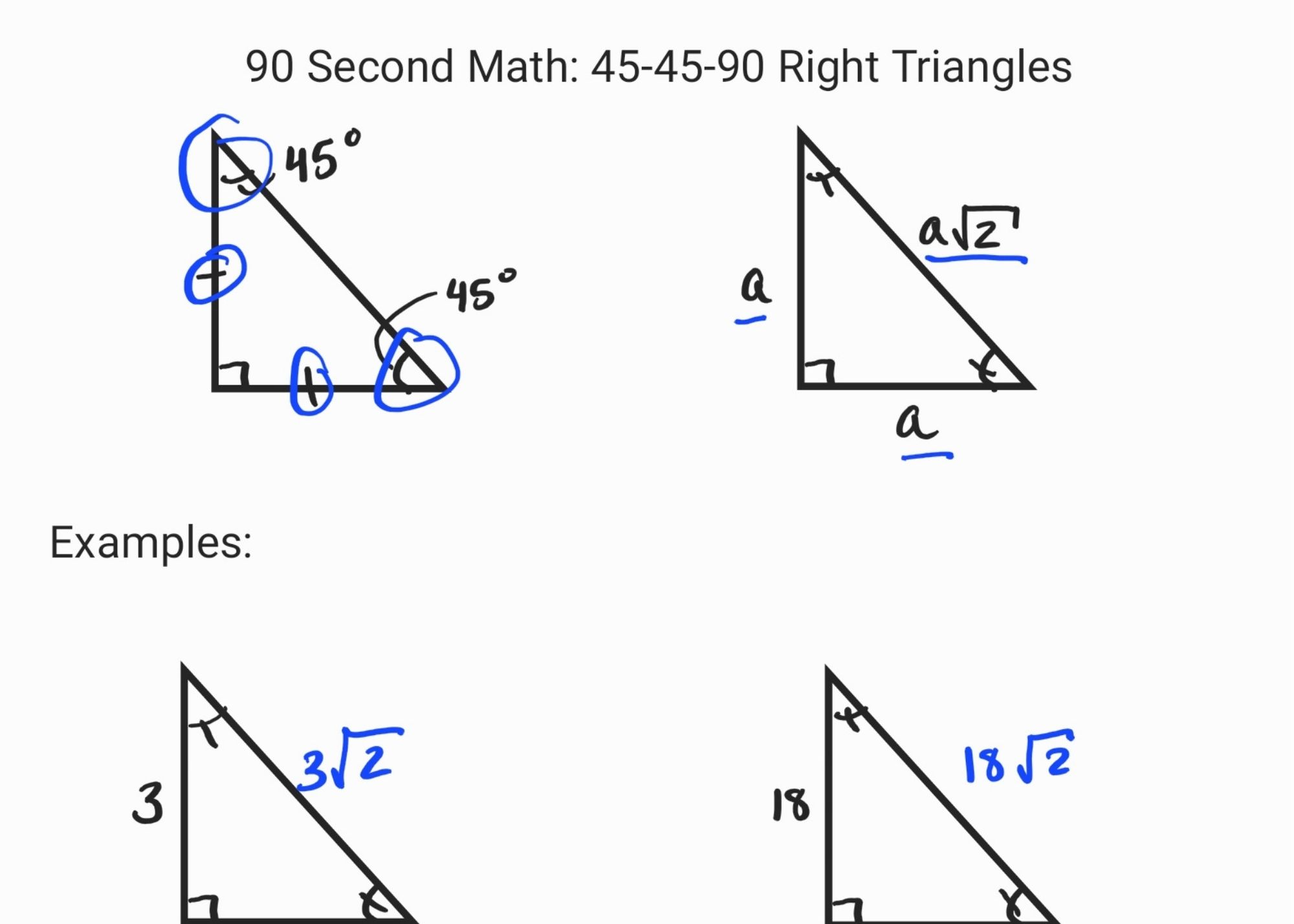
Trójkąt 45-45-90: Połowa kwadratu

A teraz zajmijmy się drugim wyjątkowym trójkątem – trójkątem 45-45-90. Wyobraź sobie kwadrat. Ma on cztery równe boki i cztery kąty proste (90 stopni). Przetnij go wzdłuż przekątnej (linia łącząca przeciwległe wierzchołki). Co otrzymasz? Dwa identyczne trójkąty prostokątne! Każdy z nich ma kąty: 45 stopni, 45 stopni i 90 stopni. Bingo! To właśnie jest trójkąt 45-45-90.

W tym trójkącie dwa boki są równe (te, które leżą przy kącie prostym). Nazwijmy je 'a'. Wtedy:

• Przeciwprostokątna (najdłuższy bok) ma długość a√2.

Przykład: Załóżmy, że każdy z boków przy kącie prostym ma długość 7 cm. Wtedy przeciwprostokątna ma długość 7√2 cm. Znowu, proste!

Wizualizacja:

Pomyśl o √2 (pierwiastek z 2) jako o takim "współczynniku powiększenia". Pomnożysz bok przez ten "współczynnik" i od razu masz długość przeciwprostokątnej.

Zastosowania w życiu codziennym:

Trójkąty 45-45-90 są szeroko stosowane w budownictwie, szczególnie przy konstrukcjach dachów. Pozwalają na precyzyjne obliczanie długości krokwi i innych elementów konstrukcyjnych. Również w stolarstwie, przy cięciu desek pod kątem 45 stopni (na przykład do ramek), znajomość właściwości tego trójkąta jest bardzo pomocna.

Rozwiązywanie zadań: Klucze do sukcesu

Teraz, kiedy już znamy te magiczne trójkąty, zobaczmy, jak możemy wykorzystać tę wiedzę do rozwiązywania zadań.

1. Zidentyfikuj trójkąt: Sprawdź, czy trójkąt jest prostokątny i czy ma kąty 30-60-90 lub 45-45-90.
2. Oznacz długości boków: Użyj 'a' jako zmiennej dla najkrótszego boku w trójkącie 30-60-90 lub dla jednego z równych boków w trójkącie 45-45-90.
3. Zastosuj wzory: Wykorzystaj zależności, które omówiliśmy wcześniej (2a, a√3, a√2), aby obliczyć długości pozostałych boków.
4. Sprawdź odpowiedź: Upewnij się, że odpowiedź ma sens w kontekście zadania. Czy najdłuższy bok jest rzeczywiście najdłuższy? Czy kąty się zgadzają?

Pamiętaj: Praktyka czyni mistrza! Im więcej zadań rozwiążesz, tym lepiej zrozumiesz te trójkąty i tym łatwiej będzie Ci z nimi pracować. Nie bój się korzystać z rysunków i diagramów – wizualizacja problemu często pomaga w znalezieniu rozwiązania.

Dodatkowa wskazówka: Czasami zadania mogą być podchwytliwe. Mogą wymagać od Ciebie łączenia wiedzy o trójkątach 30-60-90 i 45-45-90 z innymi zagadnieniami geometrycznymi, takimi jak twierdzenie Pitagorasa czy własności figur podobnych. Dlatego ważne jest, aby dobrze znać podstawy i umieć je kreatywnie stosować.

Podsumowanie: Trójkąty 30-60-90 i 45-45-90 to twoi sprzymierzeńcy w geometrii. Znając ich właściwości, możesz szybko i sprawnie rozwiązywać wiele zadań. Pamiętaj o wizualizacji, praktyce i kreatywnym podejściu, a geometria stanie się dla Ciebie przyjemnością!