Jaki Jest Wzór Na Przekątną Kwadratu
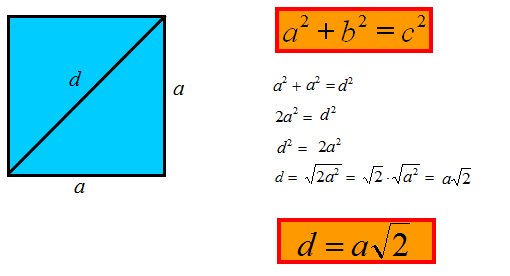
Czy kiedykolwiek zastanawiałeś się, jak szybko obliczyć długość przekątnej kwadratu, bez konieczności rysowania i mierzenia? Być może potrzebujesz tego do projektu DIY, obliczeń architektonicznych, a może po prostu z czystej ciekawości matematycznej. Niezależnie od powodu, ten artykuł jest dla Ciebie! Przybliżymy Ci prosty, ale potężny wzór na przekątną kwadratu, wyjaśniając krok po kroku jego pochodzenie i zastosowanie. Zrozumienie tego wzoru jest kluczem do rozwiązywania wielu problemów geometrycznych, a my postaramy się przedstawić go w sposób przystępny i zrozumiały dla każdego.
Dlaczego Warto Znać Wzór Na Przekątną Kwadratu?
Wzór na przekątną kwadratu to nie tylko kolejna matematyczna formułka. To narzędzie, które może ułatwić Ci życie w wielu sytuacjach. Wyobraź sobie, że projektujesz ogród i chcesz stworzyć kwadratową rabatę. Znając tylko długość boku, możesz błyskawicznie obliczyć, jak długa będzie ścieżka, która przetnie rabatę po przekątnej. Albo jesteś architektem i potrzebujesz szybko sprawdzić wymiary konstrukcji. Znajomość tego wzoru pozwoli Ci zaoszczędzić czas i uniknąć błędów.
Dzięki temu, że jest on tak łatwy w użyciu, wzór ten jest niezastąpiony w wielu dziedzinach, od geometrii i architektury, po rzemiosło i majsterkowanie. Co więcej, zrozumienie jego pochodzenia pozwala na głębsze zrozumienie zasad geometrii i buduje solidne fundamenty do dalszej nauki.
Czym Jest Kwadrat i Jego Przekątna?
Zacznijmy od podstaw. Kwadrat to czworokąt, który ma wszystkie boki równe i wszystkie kąty proste (90 stopni). Jest to figura bardzo regularna i symetryczna, co czyni ją prostą do analizy i obliczeń.
Przekątna kwadratu to odcinek łączący dwa przeciwległe wierzchołki. Każdy kwadrat ma dwie przekątne, które przecinają się w swoim środku pod kątem prostym. Co ważne, przekątna dzieli kwadrat na dwa trójkąty prostokątne równoramienne. Ta właściwość jest kluczowa do zrozumienia wzoru na jej długość.
Wzór Na Przekątną Kwadratu: Prosto i Zwięźle
A teraz najważniejsze: Wzór na przekątną kwadratu. Brzmi on następująco:
d = a√2
Gdzie:
- d oznacza długość przekątnej kwadratu.
- a oznacza długość boku kwadratu.
- √2 to pierwiastek kwadratowy z 2, który w przybliżeniu wynosi 1.4142.
Czyli, aby obliczyć długość przekątnej kwadratu, wystarczy pomnożyć długość jego boku przez pierwiastek kwadratowy z 2. Proste, prawda?
Pochodzenie Wzoru: Twierdzenie Pitagorasa w Akcji
Skąd wziął się ten wzór? Otóż, wynika on bezpośrednio z twierdzenia Pitagorasa, które mówi, że w trójkącie prostokątnym suma kwadratów długości przyprostokątnych (boków przylegających do kąta prostego) jest równa kwadratowi długości przeciwprostokątnej (boku leżącego naprzeciwko kąta prostego).
W naszym przypadku, przekątna kwadratu dzieli go na dwa trójkąty prostokątne, gdzie bok kwadratu (a) jest przyprostokątną, a przekątna (d) jest przeciwprostokątną. Zatem, możemy zapisać twierdzenie Pitagorasa dla tego trójkąta:
a² + a² = d²
Uproszczając to równanie, otrzymujemy:
2a² = d²
Aby wyznaczyć d, musimy spierwiastkować obie strony równania:
√(2a²) = √d²
Co daje nam:
a√2 = d
I oto jest! Dowód na to, że wzór na przekątną kwadratu wynika bezpośrednio z fundamentalnego twierdzenia geometrii, jakim jest twierdzenie Pitagorasa.
Przykłady Zastosowania Wzoru
Aby lepiej zrozumieć, jak działa wzór na przekątną kwadratu, rozważmy kilka przykładów:
Przykład 1: Mały Kwadrat
Załóżmy, że mamy kwadrat o boku długości 5 cm. Jak długa jest jego przekątna?
Zastosowanie wzoru: d = a√2
d = 5 cm * √2
d ≈ 5 cm * 1.4142
d ≈ 7.07 cm
Zatem przekątna kwadratu o boku 5 cm ma długość około 7.07 cm.
Przykład 2: Większy Kwadrat
A co, jeśli mamy większy kwadrat, np. o boku 12 cm? Wtedy:
d = a√2
d = 12 cm * √2
d ≈ 12 cm * 1.4142
d ≈ 16.97 cm
W tym przypadku, przekątna kwadratu o boku 12 cm ma długość około 16.97 cm.
Przykład 3: Praktyczne Zastosowanie
Wyobraź sobie, że budujesz ramkę do obrazu w kształcie kwadratu. Chcesz, aby długość ramy wynosiła 30 cm. Ile materiału potrzebujesz na przekątną, aby wzmocnić ramkę?
d = a√2
d = 30 cm * √2
d ≈ 30 cm * 1.4142
d ≈ 42.43 cm
Potrzebujesz około 42.43 cm materiału na wzmocnienie przekątnej ramki.
Kiedy Używać Wzoru i Alternatywne Metody
Wzór d = a√2 jest najbardziej przydatny, gdy znamy długość boku kwadratu i chcemy szybko obliczyć długość przekątnej. Jest to metoda szybka i precyzyjna.
Istnieją jednak sytuacje, w których możemy znać długość przekątnej i chcieć obliczyć długość boku kwadratu. Wtedy możemy przekształcić wzór:
a = d / √2
Czyli, długość boku kwadratu jest równa długości przekątnej podzielonej przez pierwiastek kwadratowy z 2.
Inną alternatywną metodą, choć mniej praktyczną w większości przypadków, jest użycie twierdzenia Pitagorasa bezpośrednio. Jeśli nie pamiętamy wzoru na przekątną, zawsze możemy obliczyć ją, rozwiązując równanie a² + a² = d².
Praktyczne Wskazówki i Triki
- Pamiętaj o jednostkach: Upewnij się, że używasz tych samych jednostek miary dla wszystkich boków (np. cm, metry, cale).
- Użyj kalkulatora: Do obliczenia pierwiastka kwadratowego z 2 użyj kalkulatora. Możesz też użyć przybliżonej wartości 1.4142, ale wynik będzie mniej dokładny.
- Zaokrąglaj wyniki: W zależności od potrzeb, zaokrąglaj wyniki do odpowiedniej liczby miejsc po przecinku.
- Sprawdzaj wyniki: Zawsze warto sprawdzić wynik, np. wizualnie, rysując kwadrat i mierząc przekątną.
Podsumowanie: Wzór na Przekątną Kwadratu w Pigułce
Podsumowując, wzór na przekątną kwadratu to potężne i przydatne narzędzie, które pozwala na szybkie i precyzyjne obliczenia. Zapamiętaj go: d = a√2. Zrozumienie jego pochodzenia, opartego na twierdzeniu Pitagorasa, pozwala na głębsze zrozumienie geometrii i buduje solidne podstawy do dalszej nauki.
Niezależnie od tego, czy jesteś uczniem, studentem, majsterkowiczem czy architektem, znajomość tego wzoru z pewnością Ci się przyda. Wykorzystaj go w swoich projektach, obliczeniach i codziennych sytuacjach. Odkryj, jak wiele problemów możesz rozwiązać dzięki tej prostej formule!
Mamy nadzieję, że ten artykuł pomógł Ci zrozumieć wzór na przekątną kwadratu i jego zastosowania. Życzymy powodzenia w korzystaniu z tej wiedzy!