Funkcje Teygonometryczne Kątów Ostrych

Wprowadzenie do funkcji trygonometrycznych kątów ostrych otwiera przed nami fascynujący świat relacji między kątami a długościami boków w trójkącie prostokątnym. Stanowią one fundament wielu dziedzin nauki i techniki, od fizyki i inżynierii po nawigację i astronomię. Zrozumienie ich działania pozwala rozwiązywać problemy, które inaczej byłyby nieosiągalne.

Podstawowe Funkcje Trygonometryczne

W trójkącie prostokątnym, gdzie jeden z kątów ma miarę 90 stopni, wyróżniamy trzy podstawowe funkcje trygonometryczne, które odnoszą się do kątów ostrych (czyli kątów mniejszych niż 90 stopni): sinus (sin), cosinus (cos) i tangens (tg lub tan).

Sinus (sin)

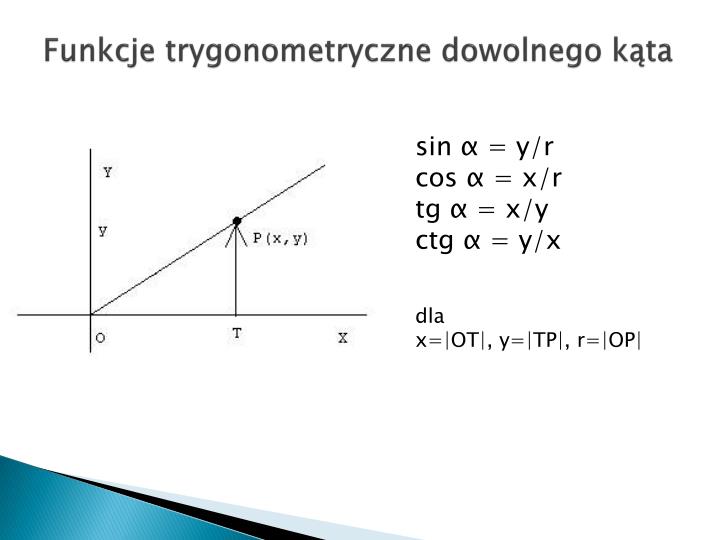
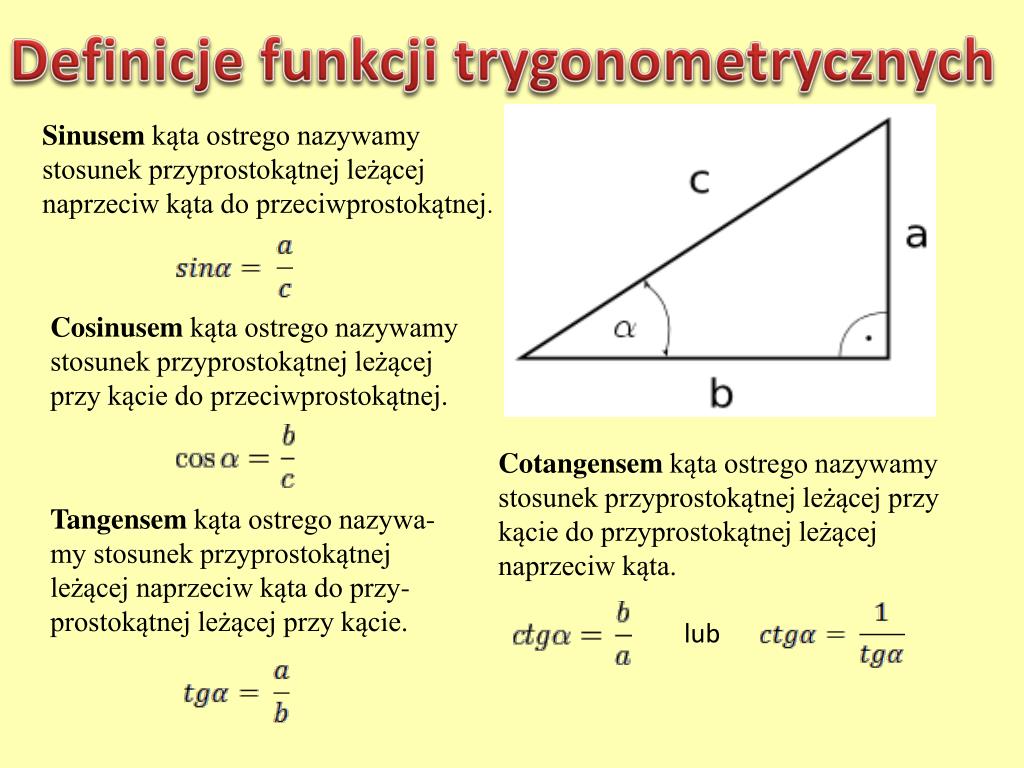
Sinus kąta ostrego definiuje się jako stosunek długości przyprostokątnej leżącej naprzeciwko kąta do długości przeciwprostokątnej. Matematycznie zapisujemy to jako:

sin(α) = długość przyprostokątnej naprzeciwko α / długość przeciwprostokątnej

Oznacza to, że jeśli znamy miarę kąta α i długość przeciwprostokątnej, możemy obliczyć długość przyprostokątnej naprzeciwko tego kąta, lub odwrotnie.

Cosinus (cos)

Cosinus kąta ostrego definiuje się jako stosunek długości przyprostokątnej przyległej do kąta do długości przeciwprostokątnej. W zapisie matematycznym:

cos(α) = długość przyprostokątnej przyległej do α / długość przeciwprostokątnej

Podobnie jak w przypadku sinusa, znajomość miary kąta i jednej z długości boków pozwala na obliczenie drugiej.

Tangens (tg lub tan)

Tangens kąta ostrego definiuje się jako stosunek długości przyprostokątnej leżącej naprzeciwko kąta do długości przyprostokątnej przyległej do kąta. Wzór wygląda następująco:

tg(α) = długość przyprostokątnej naprzeciwko α / długość przyprostokątnej przyległej do α

Tangens można również wyrazić jako stosunek sinusa do cosinusa tego samego kąta: tg(α) = sin(α) / cos(α).

Wartości Funkcji Trygonometrycznych dla Kątów Charakterystycznych

Dla pewnych kątów ostrych, takich jak 30°, 45° i 60°, wartości funkcji trygonometrycznych są dobrze znane i często wykorzystywane. Warto je zapamiętać lub mieć pod ręką tabelkę z ich wartościami:

• 30° (π/6 rad): sin(30°) = 1/2, cos(30°) = √3/2, tg(30°) = √3/3
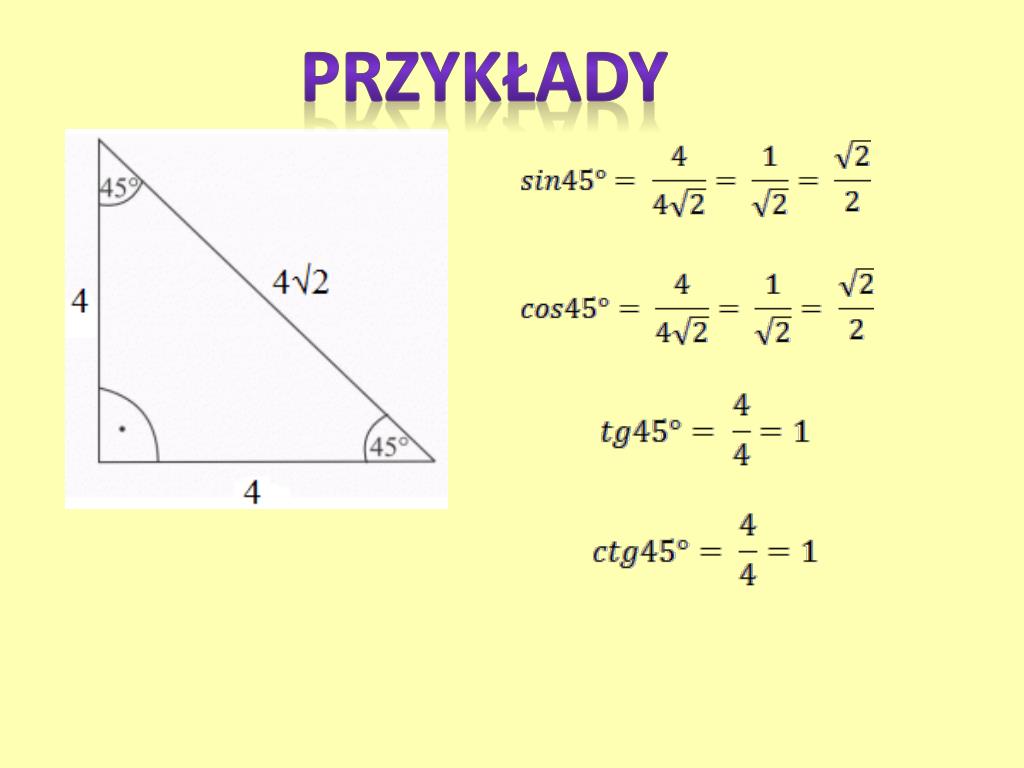
• 45° (π/4 rad): sin(45°) = √2/2, cos(45°) = √2/2, tg(45°) = 1
• 60° (π/3 rad): sin(60°) = √3/2, cos(60°) = 1/2, tg(60°) = √3

Znajomość tych wartości znacznie ułatwia rozwiązywanie wielu zadań.

Funkcje Odwrotne do Funkcji Trygonometrycznych

Oprócz podstawowych funkcji trygonometrycznych, istnieją również funkcje odwrotne, które pozwalają na wyznaczenie miary kąta, znając wartość danej funkcji. Należą do nich:

• Arcus sinus (arcsin lub sin⁻¹): Funkcja odwrotna do sinusa. arcsin(x) zwraca kąt, którego sinus wynosi x.
• Arcus cosinus (arccos lub cos⁻¹): Funkcja odwrotna do cosinusa. arccos(x) zwraca kąt, którego cosinus wynosi x.
• Arcus tangens (arctg lub tan⁻¹): Funkcja odwrotna do tangensa. arctg(x) zwraca kąt, którego tangens wynosi x.

Funkcje te są niezwykle przydatne, gdy chcemy obliczyć kąt, znając stosunek długości boków w trójkącie prostokątnym.

Praktyczne Zastosowania Funkcji Trygonometrycznych

Funkcje trygonometryczne znajdują szerokie zastosowanie w różnych dziedzinach życia. Oto kilka przykładów:

Nawigacja

W nawigacji, zarówno morskiej, jak i lotniczej, funkcje trygonometryczne są niezbędne do określania pozycji, kursu i odległości. Wykorzystuje się je do obliczeń związanych z triangulacją, gdzie znając kąty i odległość do dwóch punktów orientacyjnych, można określić położenie statku lub samolotu.

Inżynieria Budowlana

W inżynierii budowlanej funkcje trygonometryczne pomagają w projektowaniu i budowie mostów, budynków i innych konstrukcji. Są wykorzystywane do obliczania kątów nachylenia, sił działających na konstrukcję oraz do precyzyjnego ustawiania elementów konstrukcyjnych.

Fizyka

W fizyce funkcje trygonometryczne są używane do opisywania zjawisk falowych, takich jak ruch harmoniczny prosty, fale dźwiękowe i fale elektromagnetyczne. Pozwalają na analizę drgań, oscylacji i interferencji fal.

Geodezja

Geodezja, czyli nauka o pomiarach Ziemi, opiera się w dużej mierze na funkcjach trygonometrycznych. Są one wykorzystywane do pomiarów odległości, kątów i wysokości, a także do tworzenia map i planów.

Astronomia

Astronomia wykorzystuje funkcje trygonometryczne do obliczania odległości do gwiazd i planet, a także do opisywania ich ruchu po sferze niebieskiej. Znajomość kątów i odległości pozwala na określenie położenia ciał niebieskich i przewidywanie ich przyszłych pozycji.

Przykład: Obliczanie Wysokości Budynku

Załóżmy, że chcemy obliczyć wysokość budynku, stojąc w pewnej odległości od niego. Mierzymy kąt nachylenia od poziomu do szczytu budynku i odległość od budynku. Jeśli kąt nachylenia wynosi 30°, a odległość od budynku wynosi 20 metrów, możemy użyć funkcji tangens:

tg(30°) = wysokość budynku / odległość od budynku

√3/3 = wysokość budynku / 20

wysokość budynku = 20 * √3/3 ≈ 11.55 metrów

W ten sposób, wykorzystując funkcję tangens, możemy łatwo obliczyć wysokość budynku bez konieczności wchodzenia na niego.

Przykład: Dane rzeczywiste - System GPS

System GPS (Global Positioning System) używa triangulacji do określania pozycji odbiornika GPS na Ziemi. Satelity GPS wysyłają sygnały, które zawierają informacje o czasie wysłania sygnału i położeniu satelity. Odbiornik GPS mierzy czas, w jakim sygnał dotarł do niego i na podstawie różnicy czasu oblicza odległość do satelity. Mając odległości do co najmniej czterech satelitów, odbiornik GPS może, wykorzystując zaawansowane obliczenia trygonometryczne i geometryczne, dokładnie określić swoją pozycję (szerokość, długość i wysokość). Błędy pomiarowe wynikają z precyzji pomiaru czasu i dokładności położenia satelitów, ale funkcje trygonometryczne są *fundamentalne* dla działania tego systemu.

Podsumowanie i Zachęta do Dalszej Nauki

Funkcje trygonometryczne kątów ostrych są potężnym narzędziem, które pozwala na rozwiązywanie problemów w wielu dziedzinach. Ich zrozumienie i opanowanie otwiera drzwi do głębszego poznania matematyki, fizyki i innych nauk. Zachęcam do dalszego zgłębiania wiedzy na temat funkcji trygonometrycznych, poznawania ich właściwości i zastosowań. Ćwiczenia i rozwiązywanie zadań są kluczem do opanowania tej wiedzy. Pamiętaj, że matematyka jest jak język – im więcej jej używasz, tym lepiej ją rozumiesz.

Wykorzystaj tę wiedzę do analizy otaczającego Cię świata, do rozwiązywania problemów inżynieryjnych, do zrozumienia zjawisk fizycznych. Funkcje trygonometryczne są wszędzie! Powodzenia!