Droga Prędkość Czas Zadania Klasa 8

Hej ósmoklasiści! Rozwiązywanie zadań z fizyki i matematyki, które dotyczą drogi, prędkości i czasu może wydawać się trudne na początku. Ale spokojnie! Razem rozłożymy to na czynniki pierwsze i zobaczycie, że to wcale nie jest takie straszne. Zaczniemy od podstaw, wyjaśnimy sobie wszystkie pojęcia i rozwiążemy kilka przykładów. Przygotujcie się na jasne i zrozumiałe tłumaczenie!

Czym jest Droga, Prędkość i Czas?

Zanim zaczniemy rozwiązywać zadania, musimy dobrze zrozumieć, co oznaczają te trzy pojęcia.

Droga (s)

Droga to po prostu dystans, jaki pokonuje ciało (np. samochód, rowerzysta, człowiek). Mierzymy ją zazwyczaj w metrach (m), kilometrach (km), czasem w centymetrach (cm) lub milimetrach (mm). Pomyśl o drodze, którą pokonujesz idąc do szkoły. To właśnie jest Twoja droga!

Przykład: Droga z Twojego domu do szkoły wynosi 1.5 km.

Prędkość (v)

Prędkość mówi nam, jak szybko ciało pokonuje drogę. Czyli, ile drogi pokonuje w jednostce czasu. Najczęściej używane jednostki prędkości to metry na sekundę (m/s) i kilometry na godzinę (km/h). Wyobraź sobie, że biegniesz. Twoja prędkość to to, jak szybko przebiegasz dany odcinek. Im szybciej biegniesz, tym większa jest Twoja prędkość.

Przykład: Samochód jedzie z prędkością 80 km/h. To znaczy, że w ciągu jednej godziny pokonuje 80 kilometrów.

Czas (t)

Czas to po prostu okres, w którym trwa ruch. Mierzymy go w sekundach (s), minutach (min), godzinach (h). Czas to to, ile trwa Twoja droga do szkoły. Czy to 10 minut? 30 minut? To właśnie jest czas.

Przykład: Spacer do sklepu zajmuje 15 minut.

Podstawowe Wzory

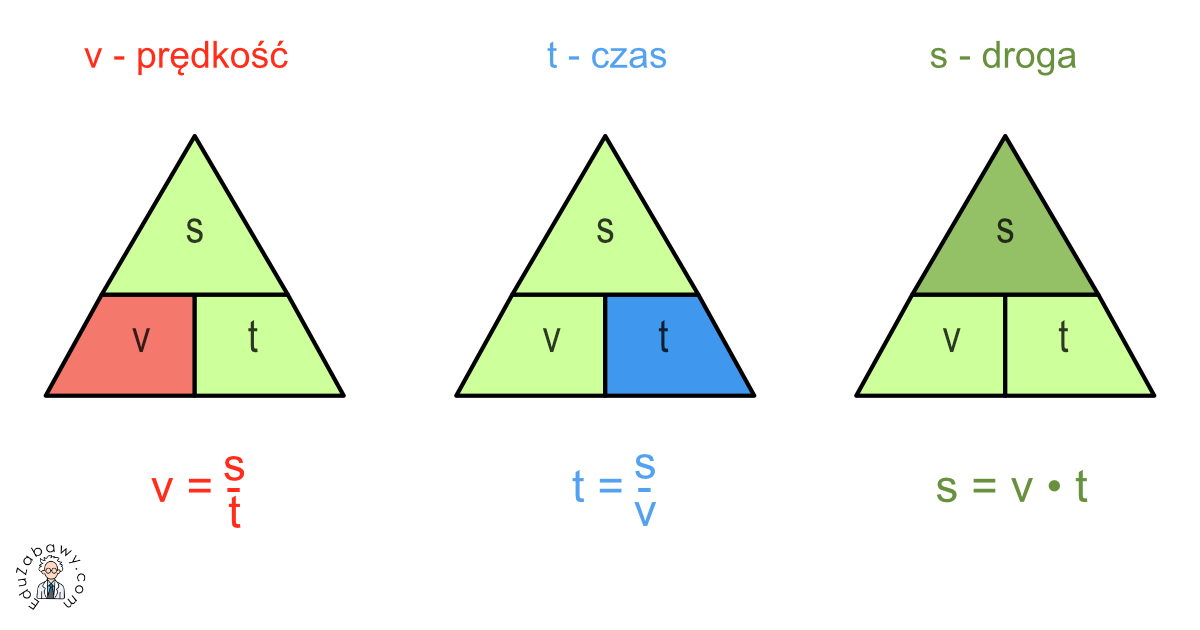
Teraz, kiedy już wiemy, co oznaczają droga, prędkość i czas, możemy przejść do najważniejszej części: wzorów. Istnieją trzy podstawowe wzory, które wiążą te wielkości ze sobą:

• Prędkość (v) = Droga (s) / Czas (t) czyli v = s / t (Prędkość jest równa drodze podzielonej przez czas)
• Droga (s) = Prędkość (v) * Czas (t) czyli s = v * t (Droga jest równa prędkości pomnożonej przez czas)
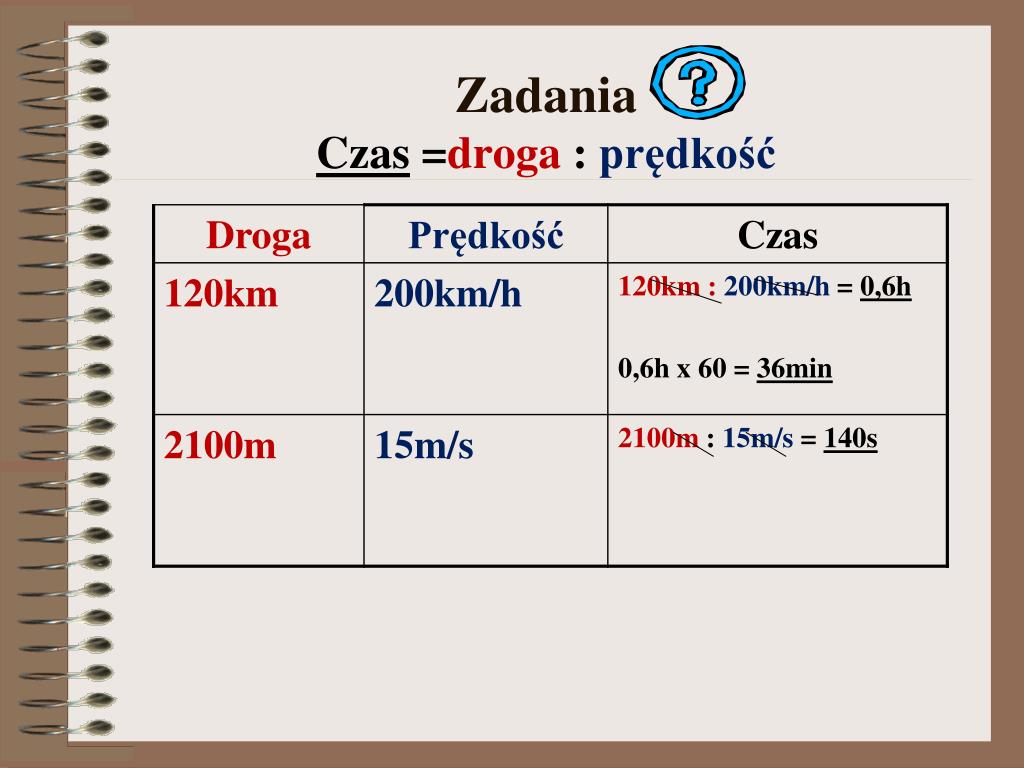
• Czas (t) = Droga (s) / Prędkość (v) czyli t = s / v (Czas jest równy drodze podzielonej przez prędkość)

Zauważ, że znając dwa z tych trzech parametrów, możemy obliczyć trzeci. To jest klucz do rozwiązywania zadań!

Przykłady Zadań i Rozwiązania

Teraz przejdźmy do konkretnych przykładów. Rozwiążemy kilka zadań krok po kroku, żebyś zobaczył, jak stosować te wzory w praktyce.

Zadanie 1:

Rowerzysta jedzie z prędkością 20 km/h przez 3 godziny. Jaką drogę pokona?

Rozwiązanie:

1. Wypisujemy dane:
   • Prędkość (v) = 20 km/h
   • Czas (t) = 3 h
   • Droga (s) = ?
2. Używamy wzoru na drogę: s = v * t
3. Podstawiamy wartości: s = 20 km/h * 3 h
4. Obliczamy: s = 60 km

Odpowiedź: Rowerzysta pokona drogę 60 km.

Zadanie 2:

Samochód przejechał 150 km w czasie 2 godzin. Z jaką prędkością jechał samochód?

Rozwiązanie:

1. Wypisujemy dane:
   • Droga (s) = 150 km
   • Czas (t) = 2 h
   • Prędkość (v) = ?
2. Używamy wzoru na prędkość: v = s / t
3. Podstawiamy wartości: v = 150 km / 2 h
4. Obliczamy: v = 75 km/h

Odpowiedź: Samochód jechał z prędkością 75 km/h.

Zadanie 3:

Pies biegnie z prędkością 10 m/s. Jak długo będzie biegł, żeby pokonać odległość 50 metrów?

Rozwiązanie:

1. Wypisujemy dane:
   • Prędkość (v) = 10 m/s
   • Droga (s) = 50 m
   • Czas (t) = ?
2. Używamy wzoru na czas: t = s / v
3. Podstawiamy wartości: t = 50 m / 10 m/s
4. Obliczamy: t = 5 s

Odpowiedź: Pies będzie biegł przez 5 sekund.

Wskazówki i Triki

• Zawsze wypisuj dane! To bardzo pomaga zorganizować informacje i zobaczyć, czego szukasz.
• Uważaj na jednostki! Upewnij się, że wszystkie wartości są wyrażone w tych samych jednostkach (np. km i h, albo m i s). Jeśli masz kilometry i sekundy, musisz coś zamienić, żeby pasowało.
• Sprawdzaj, czy wynik ma sens! Czy wynik jest realistyczny? Czy pies może biec z prędkością 1000 km/h? Raczej nie. Logiczne myślenie pomaga uniknąć błędów.
• Ćwicz! Im więcej zadań rozwiążesz, tym lepiej zrozumiesz te zagadnienia.

Zamiana Jednostek

Jak już wspomnieliśmy, ważne jest, aby pracować z odpowiednimi jednostkami. Często będziesz musiał zamieniać jednostki prędkości z km/h na m/s i odwrotnie. Oto jak to zrobić:

• km/h na m/s: Pomnóż km/h przez 1000/3600 (czyli 5/18). Na przykład: 72 km/h * (5/18) = 20 m/s
• m/s na km/h: Pomnóż m/s przez 3600/1000 (czyli 18/5). Na przykład: 25 m/s * (18/5) = 90 km/h

Podsumowanie

Pamiętaj, droga, prędkość i czas to podstawa wielu zagadnień w fizyce i matematyce. Zrozumienie tych pojęć i umiejętność stosowania odpowiednich wzorów otworzy Ci drzwi do rozwiązywania bardziej skomplikowanych problemów. Nie zrażaj się początkowymi trudnościami, ćwicz regularnie, a zobaczysz, że dasz radę! Powodzenia!