Dodawanie Liczb O Tej Samej Potędze

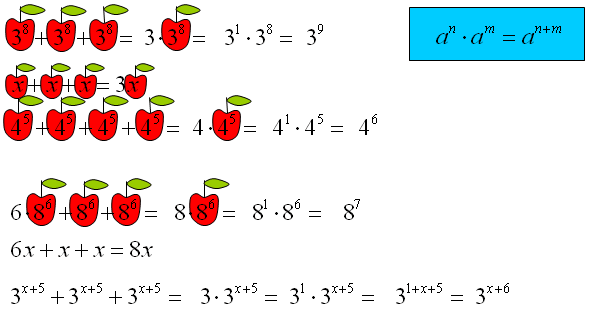
Czy kiedykolwiek zastanawiałeś się, jak efektywnie dodawać liczby, które wydają się skomplikowane ze względu na obecność potęg? Może wydawać się to wyzwaniem, ale w rzeczywistości, gdy opanujesz kilka podstawowych zasad, staje się to całkiem proste. Ten artykuł jest przeznaczony dla każdego, kto chce zrozumieć, jak dodawać liczby o tej samej potędze, od uczniów szkół podstawowych po osoby, które chcą odświeżyć swoją wiedzę matematyczną. Naszym celem jest demistyfikacja tego procesu i uczynienie go przystępnym dla wszystkich.

Wprowadzenie do potęg

Zanim przejdziemy do dodawania, zacznijmy od podstaw. Czym właściwie jest potęga? Potęga to skrócony sposób zapisu mnożenia tej samej liczby przez samą siebie. Na przykład, 2³ (czytane jako "dwa do potęgi trzeciej") oznacza 2 * 2 * 2 = 8. Liczba 2 w tym przykładzie nazywana jest podstawą potęgi, a liczba 3 to wykładnik potęgi.

Potęgi są wszechobecne w matematyce i fizyce. Wykorzystujemy je do opisywania wzrostu populacji, obliczania powierzchni i objętości, a nawet w zrozumieniu zjawisk kwantowych. Dlatego zrozumienie potęg jest kluczowe dla rozwoju umiejętności matematycznych.

Dodawanie liczb o tej samej potędze: Podstawowe zasady

Gdy mamy do czynienia z dodawaniem liczb o tej samej potędze, sprawa jest prosta, jeśli możemy sprowadzić problem do dodawania wyrazów podobnych. Co to znaczy? Oznacza to, że dodajemy tylko te wyrażenia, które mają identyczną podstawę i identyczny wykładnik.

Wyobraź sobie, że masz 3x² + 5x². Tutaj, x² jest wspólnym elementem. Możemy to potraktować jak dodawanie jabłek: 3 jabłka + 5 jabłek = 8 jabłek. Zatem, 3x² + 5x² = 8x².

Kluczowa zasada: Możemy dodawać lub odejmować tylko wyrażenia, które mają dokładnie taką samą podstawę i wykładnik. Inaczej mówiąc, możemy łączyć tylko wyrazy podobne.

Przykłady dodawania liczb o tej samej potędze

Rozważmy kilka przykładów, aby lepiej to zrozumieć:

• Przykład 1: 2³ + 5 * 2³. W tym przypadku, 2³ jest wspólnym czynnikiem. Możemy więc zapisać to jako (1 + 5) * 2³ = 6 * 2³ = 6 * 8 = 48.
• Przykład 2: 7x⁴ - 2x⁴. Tutaj mamy odejmowanie, ale zasada jest ta sama. (7 - 2) * x⁴ = 5x⁴.
• Przykład 3: a⁵ + 3a⁵ + 2a⁵. Dodajemy wszystkie współczynniki przed a⁵: (1 + 3 + 2) * a⁵ = 6a⁵.

Co zrobić, gdy potęgi są różne?

Jeśli potęgi są różne, nie możemy ich bezpośrednio dodawać. Musimy albo uprościć wyrażenia do postaci, w której mają taką samą potęgę (jeśli to możliwe), albo po prostu obliczyć wartość każdej potęgi osobno i dodać wyniki.

Na przykład, jeśli mamy 2² + 2³, nie możemy ich bezpośrednio dodać. Musimy obliczyć każdą z nich osobno: 2² = 4 i 2³ = 8. Następnie dodajemy wyniki: 4 + 8 = 12.

Przykłady z różnymi potęgami

• Przykład 1: 3² + 3³ = 9 + 27 = 36.
• Przykład 2: x² + x³. W tym przypadku, nie możemy nic zrobić, chyba że znamy wartość x. To wyrażenie pozostaje w takiej postaci: x² + x³.

Zaawansowane techniki i pułapki

Czasami problem może być bardziej skomplikowany i wymagać zastosowania dodatkowych technik. Na przykład, możemy potrzebować wyciągnąć wspólny czynnik przed nawias, aby sprowadzić wyrażenia do postaci z taką samą potęgą.

Rozważmy wyrażenie: 2x³ + 4x². W tym przypadku, możemy wyciągnąć 2x² przed nawias: 2x²(x + 2). Teraz mamy uproszczone wyrażenie, ale nadal nie możemy go "dodać" w tradycyjnym sensie, chyba że znamy wartość x.

Pułapki:

• Pamiętaj, że nie możesz dodawać potęg, jeśli nie mają tej samej podstawy i wykładnika.
• Uważaj na znaki! Upewnij się, że prawidłowo uwzględniasz znaki plus i minus.
• Nie zapomnij o kolejności działań (PEMDAS/BODMAS): nawiasy, potęgi, mnożenie i dzielenie, dodawanie i odejmowanie.

Praktyczne zastosowania

Dodawanie liczb o tej samej potędze jest nie tylko abstrakcyjnym ćwiczeniem matematycznym. Ma wiele praktycznych zastosowań w różnych dziedzinach, takich jak:

• Inżynieria: Obliczanie wytrzymałości konstrukcji, analizowanie obwodów elektrycznych.
• Fizyka: Modelowanie ruchu, obliczanie energii.
• Informatyka: Algorytmy, grafika komputerowa.
• Finanse: Obliczanie procentu składanego, analiza wzrostu inwestycji.

Na przykład, w fizyce, energia kinetyczna obiektu jest proporcjonalna do kwadratu jego prędkości (E = 1/2 * mv²). Jeśli mamy kilka obiektów o różnych masach i prędkościach, możemy użyć dodawania liczb o tej samej potędze (v²) do obliczenia całkowitej energii kinetycznej.

Ćwiczenia

Aby utrwalić wiedzę, spróbuj rozwiązać poniższe ćwiczenia:

1. 4y³ + 7y³ = ?
2. 9a⁶ - 3a⁶ = ?
3. 2⁴ + 3 * 2⁴ = ?
4. 5x² + 2x³ = ? (Czy możesz to uprościć?)

Podsumowanie

Dodawanie liczb o tej samej potędze jest prostym procesem, który wymaga zrozumienia pojęcia wyrazów podobnych. Możemy dodawać tylko te wyrażenia, które mają identyczną podstawę i identyczny wykładnik. Jeśli potęgi są różne, musimy je obliczyć osobno lub uprościć wyrażenia do postaci z taką samą potęgą (jeśli to możliwe).

Opanowanie tej umiejętności jest kluczowe dla dalszego rozwoju w matematyce i jej zastosowaniach w różnych dziedzinach. Pamiętaj, że praktyka czyni mistrza. Im więcej ćwiczysz, tym łatwiej będzie Ci rozwiązywać nawet najbardziej skomplikowane problemy.

Mam nadzieję, że ten artykuł pomógł Ci zrozumieć, jak dodawać liczby o tej samej potędze. Pamiętaj, że matematyka to przygoda, a każdy krok w przód to powód do dumy!

Powodzenia w dalszej nauce!