ćwiczenia Ułamki Dziesiętne Klasa 5

Drodzy nauczyciele klas piątych! Witamy w przewodniku po nauczaniu jednego z kluczowych, a czasem sprawiających trudności tematów: Ułamki Dziesiętne. Celem tego artykułu jest dostarczenie Wam praktycznych wskazówek, metod i strategii, które pomogą Waszym uczniom zrozumieć i polubić ułamki dziesiętne. Przyjrzymy się typowym błędom uczniów, a także sposobom na uatrakcyjnienie lekcji.

Wprowadzenie do Ułamków Dziesiętnych: Fundamenty Zrozumienia

Zanim przejdziemy do bardziej złożonych operacji, ważne jest, aby uczniowie solidnie zrozumieli, czym są ułamki dziesiętne. Kluczowe jest powiązanie ich z ułamkami zwykłymi o mianownikach będących potęgami liczby 10 (10, 100, 1000, itd.).

Praktyczne wskazówki:

Użyj reprezentacji wizualnych: Wykorzystaj modele dziesiętne, takie jak kwadraty podzielone na 100 części (setne), paski podzielone na 10 części (dziesiąte) i pojedyncze kostki reprezentujące jedności. Pozwól uczniom manipulować nimi, aby fizycznie reprezentować ułamki dziesiętne.
Połącz z systemem dziesiętnym: Podkreśl, że ułamki dziesiętne są rozszerzeniem systemu dziesiętnego o miejsca po przecinku. Wyjaśnij, że każda pozycja po przecinku reprezentuje potęgę liczby 10, np. dziesiąte części, setne części, tysięczne części.
Użyj tabeli wartości miejsc: Wprowadź tabelę wartości miejsc, która wyraźnie pokazuje, gdzie znajdują się jedności, dziesiątki, setki oraz dziesiąte, setne, tysięczne części. To wizualne narzędzie pomaga uczniom zrozumieć wartość każdej cyfry w ułamku dziesiętnym.
Mów językiem codziennym: Używaj przykładów z życia codziennego, takich jak pieniądze (złote i grosze), pomiary długości (metry i centymetry), czy waga (kilogramy i gramy). To pomaga uczniom zobaczyć, że ułamki dziesiętne są użyteczne i realne.

Typowe Błędy i Jak Im Zapobiegać

Uczniowie często popełniają błędy, które wynikają z niepełnego zrozumienia koncepcji ułamków dziesiętnych. Oto kilka najczęstszych problemów i strategie, jak je rozwiązać:

Porównywanie ułamków dziesiętnych: Często uczniowie myślą, że ułamek z większą liczbą cyfr po przecinku jest większy, np. uważają, że 0,25 jest mniejsze niż 0,3. Jak zapobiegać? Podkreśl, że ważne jest porównywanie cyfr w odpowiednich miejscach wartości. Pomóż uczniom dopisywać zera na końcu ułamków, aby miały tyle samo cyfr po przecinku, np. porównaj 0,25 z 0,30. Użyj wizualizacji, np. na osi liczbowej.
Dodawanie i odejmowanie ułamków dziesiętnych: Błędy wynikają z nieprawidłowego wyrównywania przecinków. Jak zapobiegać? Zawsze podkreślaj, że przecinki muszą być wyrównane pionowo. Wykorzystaj kartkę w kratkę, aby wizualnie pomóc uczniom w poprawnym zapisie.
Traktowanie przecinka jako separatora dwóch liczb całkowitych: Uczniowie mogą widzieć 2,5 jako oddzielne liczby 2 i 5, zamiast rozumieć, że to jedna liczba. Jak zapobiegać? Wyjaśnij, że przecinek dziesiętny oddziela część całkowitą od części ułamkowej, a obie tworzą jedną całość. Ponownie, użyj modeli dziesiętnych, aby pokazać, że 2,5 to dwie całe jednostki i połowa kolejnej jednostki.
Brak zrozumienia wartości miejsca po przecinku: Uczniowie mogą nie rozumieć, że 0,1 to dziesiąta część, a 0,01 to setna część. Jak zapobiegać? Poświęć czas na dokładne omówienie wartości miejsc po przecinku, używając tabeli wartości miejsc i wizualnych modeli.

Uatrakcyjnianie Nauki Ułamków Dziesiętnych

Nauka ułamków dziesiętnych nie musi być nudna. Oto kilka pomysłów na uatrakcyjnienie lekcji:

Gry i zabawy: Wykorzystaj gry planszowe, karty, domino, czy gry online, które wymagają używania ułamków dziesiętnych. Przykłady: "Ułamkowe bingo", "Wyścig ułamków", "Memory z ułamkami".
Projekty praktyczne: Poproś uczniów o wykonanie projektu, w którym będą musieli użyć ułamków dziesiętnych. Przykłady: zmierzenie i zważenie różnych przedmiotów, obliczenie kosztów zakupów, stworzenie przepisu kulinarnego z użyciem miar dziesiętnych.
Wykorzystanie technologii: Użyj interaktywnych zasobów online, aplikacji edukacyjnych, czy programów do wizualizacji ułamków dziesiętnych.
Uczenie przez odkrywanie: Zamiast podawać gotowe rozwiązania, stwórz sytuacje problemowe, w których uczniowie będą musieli sami dojść do wniosków dotyczących ułamków dziesiętnych.

Działania na Ułamkach Dziesiętnych: Dodawanie, Odejmowanie, Mnożenie i Dzielenie

Po opanowaniu podstaw, przechodzimy do operacji arytmetycznych. Kluczem jest konsekwencja w stosowaniu jasnych reguł i przykładów.

Dodawanie i Odejmowanie

Jak już wspomniano, wyrównywanie przecinków jest tutaj najważniejsze. Można użyć graficznego przedstawienia na kartce w kratkę, albo uczyć dopisywania zer, aby każdy ułamek miał tyle samo miejsc po przecinku.

Mnożenie

Wyjaśnij, że mnożymy jakby przecinka nie było, a następnie wstawiamy go w wyniku, licząc od prawej strony tyle miejsc, ile łącznie było w obu mnożonych liczbach. Można zacząć od mnożenia ułamka dziesiętnego przez liczbę całkowitą, a potem przejść do mnożenia dwóch ułamków dziesiętnych.

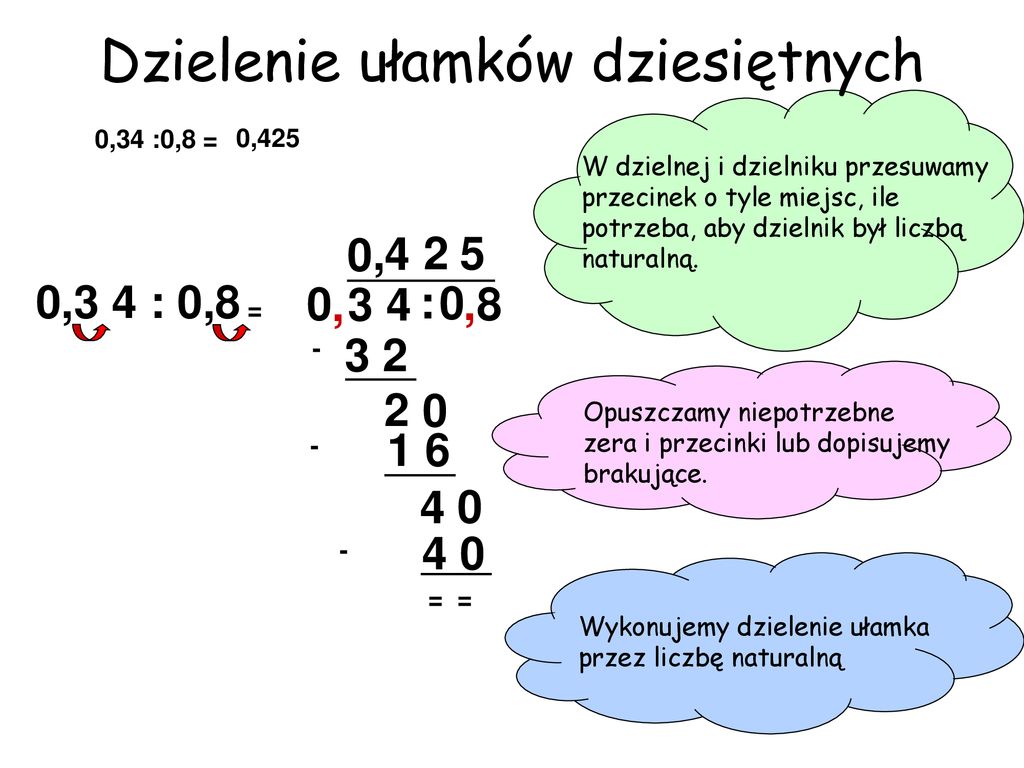
Dzielenie

Dzielenie ułamka dziesiętnego przez liczbę całkowitą jest stosunkowo proste. Ważne jest, aby przecinek w wyniku postawić dokładnie nad przecinkiem w dzielnej. Dzielenie przez ułamek dziesiętny wymaga usunięcia przecinka z dzielnika (przesunięcia przecinka w prawo), a następnie przesunięcia przecinka w dzielnej o tyle samo miejsc w prawo. Jeśli zajdzie potrzeba, dopisujemy zera.

Podsumowanie

Nauczanie ułamków dziesiętnych w klasie 5. wymaga cierpliwości, kreatywności i zrozumienia trudności, z jakimi mierzą się uczniowie. Wykorzystując wizualizacje, przykłady z życia codziennego, gry i zabawy, oraz systematyczne podejście do działań arytmetycznych, możecie pomóc swoim uczniom zbudować solidne fundamenty wiedzy matematycznej. Pamiętajcie, że zrozumienie jest ważniejsze niż zapamiętywanie reguł. Powodzenia!