Skracanie I Rozszerzanie Ułamków Zadania

W świecie matematyki, ułamki odgrywają kluczową rolę. Pozwalają nam precyzyjnie opisywać części całości, proporcje i stosunki. Zrozumienie operacji na ułamkach, takich jak skracanie i rozszerzanie, jest fundamentem dalszej nauki matematyki i ma praktyczne zastosowanie w życiu codziennym.

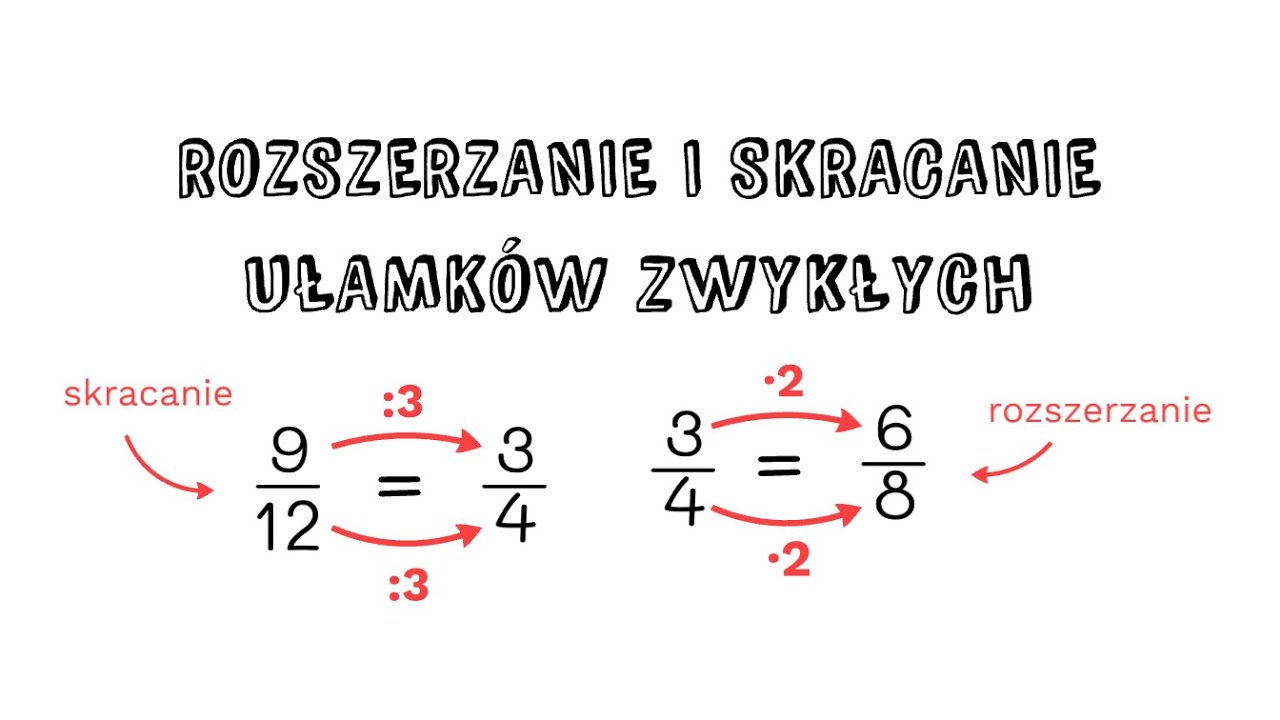
Skracanie Ułamków: Upraszczanie do Najprostszej Formy

Skracanie ułamka to proces redukowania go do najprostszej formy, w której licznik i mianownik nie mają już wspólnych dzielników innych niż 1. Celem jest uzyskanie ułamka równoważnego, ale z mniejszymi liczbami, co ułatwia dalsze obliczenia i interpretację.

Jak Skracać Ułamki?

Proces skracania opiera się na znalezieniu Największego Wspólnego Dzielnika (NWD) licznika i mianownika. NWD to największa liczba, która dzieli zarówno licznik, jak i mianownik bez reszty. Następnie, dzielimy licznik i mianownik przez NWD, aby uzyskać ułamek w najprostszej formie.

Przykład: Rozważmy ułamek ¹²/₁₈. Aby go skrócić, musimy znaleźć NWD liczb 12 i 18. Dzielniki liczby 12 to: 1, 2, 3, 4, 6, 12. Dzielniki liczby 18 to: 1, 2, 3, 6, 9, 18. Największym wspólnym dzielnikiem jest 6. Zatem, dzielimy licznik i mianownik przez 6: ^{12 ÷ 6}/_{18 ÷ 6} = ²/₃. Ułamek ²/₃ jest najprostszą formą ułamka ¹²/₁₈.

Alternatywna metoda: Można również skracać ułamek krok po kroku, dzieląc licznik i mianownik przez wspólne czynniki, aż do uzyskania najprostszej formy. W przypadku ¹²/₁₈, można najpierw podzielić przez 2: ⁶/₉, a następnie przez 3: ²/₃.

Dlaczego Skracanie Jest Ważne?

Upraszcza Obliczenia: Praca z mniejszymi liczbami jest zazwyczaj łatwiejsza i mniej podatna na błędy.
Ułatwia Porównywanie Ułamków: Skracanie ułamków do najprostszej formy pozwala łatwiej porównać je z innymi ułamkami.
Poprawia Zrozumienie: Uproszczona forma ułamka często lepiej oddaje proporcję lub stosunek, który reprezentuje.

Rozszerzanie Ułamków: Zwiększanie Mianownika i Licznika

Rozszerzanie ułamka to proces mnożenia licznika i mianownika przez tę samą liczbę różną od zera. Wynikiem jest ułamek równoważny, ale z większymi liczbami w liczniku i mianowniku.

Jak Rozszerzać Ułamki?

Aby rozszerzyć ułamek, wybieramy liczbę (czynnik rozszerzający) i mnożymy przez nią zarówno licznik, jak i mianownik. Ważne jest, aby mnożyć obie części ułamka przez tę samą liczbę, aby zachować jego wartość.

Przykład: Rozszerzmy ułamek ¹/₄ przez 3. Mnożymy licznik i mianownik przez 3: ^{1 × 3}/_{4 × 3} = ³/₁₂. Ułamek ³/₁₂ jest równoważny ułamkowi ¹/₄.

Kiedy Rozszerzać Ułamki?

Sprowadzanie do Wspólnego Mianownika: Rozszerzanie ułamków jest niezbędne, gdy chcemy porównać lub dodać/odjąć ułamki o różnych mianownikach. Musimy sprowadzić je do wspólnego mianownika, rozszerzając je odpowiednio.
Przedstawienie Proporcji w Innej Skali: W niektórych sytuacjach, chcemy przedstawić daną proporcję w większej lub mniejszej skali, co wymaga rozszerzenia lub skrócenia ułamka.
Upraszczanie Dalszych Obliczeń: W specyficznych przypadkach, rozszerzenie ułamka może ułatwić kolejne obliczenia, na przykład, jeśli chcemy zamienić ułamek na procent.

Praktyczne Zastosowania Skracania i Rozszerzania Ułamków

Umiejętność skracania i rozszerzania ułamków znajduje szerokie zastosowanie w różnych dziedzinach życia:

Gotowanie i Przepisy: Często musimy dostosować przepisy kulinarne, zmieniając proporcje składników. Skracanie i rozszerzanie ułamków pozwala nam na dokładne przeliczenie ilości składników. Na przykład, jeśli przepis zakłada użycie ¹/₂ szklanki mąki, a chcemy podwoić przepis, musimy rozszerzyć ułamek do ²/₄, co odpowiada 1 szklance mąki.
Finanse Osobiste: Obliczanie procentów, rabatów, czy podziału budżetu wymaga sprawnego operowania na ułamkach. Na przykład, jeśli otrzymujemy rabat 25% na produkt, możemy to przedstawić jako ułamek ²⁵/₁₀₀, który możemy skrócić do ¹/₄.
Budownictwo i Inżynieria: W projektach budowlanych często spotykamy się z wymiarami wyrażonymi w ułamkach. Przeliczanie skali, obliczanie powierzchni i objętości wymaga umiejętności operowania na ułamkach, w tym skracania i rozszerzania.
Analiza Danych i Statystyka: Prezentacja danych statystycznych często obejmuje użycie ułamków i proporcji. Skracanie ułamków pozwala na czytelne przedstawienie wyników. Na przykład, jeśli 80 ze 100 osób preferuje dany produkt, możemy to przedstawić jako ułamek ⁸⁰/₁₀₀, który można skrócić do ⁴/₅, co jest bardziej zrozumiałe.

Przykład z życia wzięty: Wyobraźmy sobie, że pieczemy ciasto i mamy przepis na ²/₃ szklanki cukru. Okazuje się, że mamy tylko miarkę o pojemności ¹/₆ szklanki. Ile takich miarek musimy użyć? Aby to obliczyć, musimy rozszerzyć ułamek ²/₃ do ułamka o mianowniku 6. Rozszerzamy przez 2: ^{2 × 2}/_{3 × 2} = ⁴/₆. Oznacza to, że potrzebujemy 4 miarek o pojemności ¹/₆ szklanki.

Błędy, Których Należy Unikać

Podczas skracania i rozszerzania ułamków łatwo o pomyłkę. Najczęstsze błędy to:

Dzielenie/Mnożenie tylko licznika lub mianownika: Należy zawsze pamiętać, aby dzielić lub mnożyć zarówno licznik, jak i mianownik przez tę samą liczbę.
Skracanie ułamków przez odejmowanie lub dodawanie: Skracanie i rozszerzanie polega na dzieleniu/mnożeniu, a nie na dodawaniu/odejmowaniu.
Brak znajomości NWD: Trudności ze znalezieniem NWD mogą uniemożliwić skuteczne skrócenie ułamka.

Podsumowanie i Wezwanie do Działania

Skracanie i rozszerzanie ułamków to fundamentalne umiejętności matematyczne, które mają praktyczne zastosowanie w wielu aspektach naszego życia. Zrozumienie tych operacji pozwala na precyzyjne obliczenia, ułatwia porównywanie proporcji i upraszcza rozwiązywanie problemów. Pamiętaj, że praktyka czyni mistrza! Ćwicz regularnie, rozwiązuj zadania i szukaj okazji do wykorzystania tej wiedzy w życiu codziennym. Im więcej ćwiczysz, tym łatwiej i szybciej będziesz mógł operować na ułamkach, a matematyka stanie się Twoim sprzymierzeńcem!

Wykorzystaj tę wiedzę do rozwiązania problemów, które napotykasz w codziennym życiu. Pomóż swoim dzieciom w nauce. Dziel się zdobytą wiedzą z innymi. Matematyka jest wszędzie! Powodzenia!